TO APPEAR IN IEEE TRANS. SIGNAL PROCESSING Covariance...
Transcript of TO APPEAR IN IEEE TRANS. SIGNAL PROCESSING Covariance...

TO APPEAR IN IEEE TRANS. SIGNAL PROCESSING 1
Covariance, Subspace, and IntrinsicCramer-Rao Bounds
Steven T. Smith*,Senior Member, IEEE
Abstract— Cramer-Rao bounds on estimation accuracy areestablished for estimation problems on arbitrary manifolds inwhich no set of intrinsic coordinates exists. The frequentlyencountered examples of estimating either an unknown subspaceor a covariance matrix are examined in detail. The set of sub-spaces, called the Grassmann manifold, and the set of covariance(positive-definite Hermitian) matrices have no fixed coordinatesystem associated with them and do not possess a vector spacestructure, both of which are required for deriving classicalCramer-Rao bounds. Intrinsic versions of the Cramer-Rao boundon manifolds utilizing an arbitrary affine connection with arbi-trary geodesics are derived for both biased and unbiased estima-tors. In the example of covariance matrix estimation, closed-formexpressions for both the intrinsic and flat bounds are derivedand compared with the root-mean-square error (RMSE) of thesample covariance matrix (SCM) estimator for varying samplesupport K. The accuracy bound on unbiased covariance matrixestimators is shown to be about(10/ log 10)n/K1/2 decibels,wheren is the matrix order. Remarkably, it is shown that from anintrinsic perspective the SCM is a biased and inefficient estimatorand that the bias term reveals the dependency of estimationaccuracy on sample support observed in theory and practice.The RMSE of the standard method of estimating subspaces usingthe singular value decomposition (SVD) is compared with theintrinsic subspace Cramer-Rao bound derived in closed-form byvarying both the signal-to-noise ratio (SNR) of the unknownp-dimensional subspace and the sample support. In the simplestcase, the Cramer-Rao bound on subspace estimation accuracyis shown to be about
`p(n − p)
´1/2K−1/2SNR−1/2 radians
for p-dimensional subspaces. It is seen that the SVD-basedmethod yields accuracies very close to the Cramer-Rao bound,establishing that the principal invariant subspace of a randomsample provides an excellent estimator of an unknown subspace.The analysis approach developed is directly applicable to manyother estimation problems on manifolds encountered in signalprocessing and elsewhere, such as estimating rotation matricesin computer vision and estimating subspace basis vectors in blindsource separation.
Index Terms— Estimation bounds, sample covariance matrix,singular value decomposition, intrinsic geometry, estimator bias,Fisher information, efficiency, Riemannian manifold, reductivehomogeneous space, natural invariant metric, positive definitematrices, Hermitian matrix, symmetric matrix, Grassmann man-ifold, differential geometry, exponential map, natural gradient,sectional and Riemannian curvature
I. I NTRODUCTION
ESTIMATION PROBLEMS are typically posed and an-alyzed for a set of fixed parameters, such as angle and
Doppler. In contrast, estimation problems on manifolds, where
Manuscript received June 23, 2003; revised January 25, 2005.*MIT Lincoln Laboratory, Lexington, MA 02420; [email protected]. This
work was sponsored by the United States Air Force under Air Force contractF19628-00-C-0002. Opinions, interpretations, conclusions, and recommenda-tions are those of the author and are not necessarily endorsed by the UnitedStates Government.
no such set of intrinsic coordinates exists, are frequentlyencountered in signal processing applications and elsewhere.Two common examples are estimating either an unknowncovariance matrix or a subspace. Because neither the set ofcovariance (positive definite Hermitian) matrices nor the setof subspaces (the Grassmann manifold) are equipped withan intrinsic coordinate system or a vector space structure,classical Cramer-Rao bound (CRB) analysis [17], [53] is notdirectly applicable. To address this class of problems, anintrinsic treatment of Cramer-Rao analysis specific to signalprocessing problems is established here. Intrinsic versions ofthe Cramer-Rao bound have also been developed for Rie-mannian manifolds [33], [41], [42], [44], [49], [50], [65],[76], [77], statistical manifolds [5], and for the applicationof quantum inference [11], [51].
The original contributions of this paper are: (1) a deriva-tion of biased and unbiased intrinsic Cramer-Rao bounds forsignal processing and related fields; (2) a new proof of theCramer-Rao bound (Theorem 2) that connects the inverseof the Fisher information matrix with its appearance in the(natural) gradient of the log-likelihood function; (3) severalresults [Theorem 4, Corollary 5, Eq. (143)] that bound theestimation accuracy of an unknown covariance matrix orsubspace; (4) the noteworthy discovery that from an intrinsicperspective, the sample covariance matrix (SCM) is a biasedand inefficient estimator (Theorem 7), and the fact that thebias corresponds to the SCM’s poor estimation quality atlow sample support (Corollary 5)—this contradicts the well-known fact thatE [R] = R because the linear expectationoperator implicitly treats the covariance matrices as a convexcone included in the vector spaceRn2
, compared to theintrinsic treatment of the covariance matrices in this paper;(5) a generalization of the expression for Fisher information(Theorem 1) that employs the Hessian of the log-likelihoodfunction for arbitrary affine connections—a useful tool becausein the great majority of applications the second-order terms aremuch easier to compute; (6) a geometric treatment of covari-ance matrices as the quotient spacePn
∼= Gl(n,C)/U(n)(i.e., the Hermitian part of the matrix polar decomposition),including a natural distance between covariance matrices thathas not appeared previously in the signal processing literature;and (7) a comparison between the accuracy of the standardsubspace estimation method employing the singular valuedecomposition (SVD) and the Cramer-Rao bound for subspaceestimation.
In contrast to previous literature on intrinsic Cramer-Raoanalysis, it is shown explicitly how to compute practicalestimation bounds on a parameter space defined by a manifold,independently of any particular metric or affine structure. As

2 TO APPEAR IN IEEE TRANS. SIGNAL PROCESSING
elsewhere, the standard approach is used to generalize classicalbounds to Riemannian manifolds via the exponential map,i.e., geodesics emanating from the estimate to points in theparameter space. Just as with classical bounds, the unbiasedintrinsic Cramer-Rao bounds depend asymptotically only onthe Fisher information and do not depend in any nontrivial wayon the choice of measurement units, e.g., feet versus meters.Though the mathematical concepts used throughout the paperare well known to the differential geometry community, a briefinformal background of the key ideas is provided in footnotesfor readers unfamiliar with some of the technicalities, as is atable at the end of the paper (page 19) comparing the generalconcepts to their more familiar counterparts inRn.
The results developed in this paper are general enough to beapplied to the numerous estimation problems on manifolds thatappear in the literature. Zheng and Tse [79], in a geometricapproach to the analysis of Hochwald and Marzetta [34],compute channel capacities for communications problems withan unknown propagation gain matrix represented by an ele-ment on the Grassmann manifold. Grenander et al. [29] deriveHilbert-Schmidt lower bounds for estimating points on a Liegroup for automatic target recognition. Srivastava [67] appliesBayesian estimation theory to subspace estimation, and Sri-vastava and Klassen [68], [69] develop an extrinsic approachto the problem of estimating points on a manifold, specificallyLie groups and their quotient spaces (including the Grassmannmanifold), and apply their method to estimating target pose.Bhattacharya and Patrangenaru [9] treat the general problem ofestimation on Riemannian manifolds. Estimating points on therotation group, or the finite product space of the rotation group,occurs in several diverse applications. Ma et al. [39] describea solution to the motion recovery problem in computer vision,and Adler et al. [2] use a set of rotations to describe amodel for the human spine. Douglas et al. [20], Smith [63],and many others [21], [22] develop gradient-based adaptivealgorithms using the natural metric structure of a constrainedspace. For global estimation bounds rather than the localones developed in this paper, Rendas and Moura [56] definea general ambiguity function for parameters in a statisticalmanifold. In the area of blind signal processing, Cichockiet al. [14], [15], Douglas [19], Rahbar and Reilly [52] solveestimation problems on the Stiefel manifold to accomplishblind source separation, and Xavier [76] analyzes blind MIMOsystem identification problems using an intrinsic approach.Readers may also be interested in the central role playedby geometrical statistical analysis in establishing Wegener’stheory of continental drift [18], [26], [41].
A. A Model Estimation Problem
Consider the problem [65] of estimating the unknownn-by-p matrix Y, n ≥ p, given the statistical model
z = Yn1 + n0 (1)
where n1 ∼ Np(0,R1) is a p-dimensional normal randomvector with zero mean and unknown covariance matrixR1,andn0 ∼ Nn(0,R0) is ann-dimensional normal random vec-tor independent ofn1 with zero mean and known covariance
matrix R0. The normal random vectorz ∼ Nn(0,R2) haszero mean and covariance matrix
E [zzT] = R2 = YR1YT + R0. (2)
Such problems arise, for example, when there is an inter-ference termYn1 with fewer degrees of freedom than thenumber of available sensors [16], [63]. Cramer-Rao boundsfor estimation problems in this form are well known [7],[57]: the Fisher information matrix for the unknown pa-rametersθ1, θ2, . . . , θn is given by the simple expres-sion (G)ij = tr
(R−1
2 (∂R2/∂θi)R−1
2 (∂R2/∂θj)), and G−1
provides the so-called stochastic CRB. What differs in theestimation problem of Eq. (1) from the standard case is anexplanation of the derivative terms when the parameters lieon a manifold. The analysis of this problem may be viewedin the context of previous analysis of subspace estimationand superresolution methods [29], [67], [69]–[71], [73], [74].This paper addresses both the real-valued and (proper [47])complex-valued cases, also referred to as the real symmetricand Hermitian cases, respectively. All real-valued examplesmay be extended to (proper) in-phase plus quadrature data byreplacing transposition with conjugate transposition and usingthe real representation of the unitary group.
B. Invariance of the Model Estimation Problem
The estimation problem of Eq. (1) is invariant to thetransformations
Y 7→ YA−1, R1 7→ AR1AT (3)
for anyp-by-p invertible matrixA in Gl(p), the general lineargroup of realp-by-p invertible matrices. That is, substitutingY := YA−1 andn1 := An1 into Eq. (1) leaves the measure-ment z unchanged. The only invariant of the transformationY 7→ YA−1 is the column span of the matrixY, and thepositive-definite symmetric (Hermitian) structure of covari-ance matrices is, of course, invariant to the transformationR1 7→ AR1AT. Therefore, only the column span ofY andthe covariance matrix ofz may be measured, and we askhow accurately we are able to estimate this subspace, i.e., thecolumn span ofY, in the presence of the unknown covariancematrix R1.
The parameter space for this estimation problem is the set ofall p-dimensional subspaces inRn, known as the Grassmannmanifold Gn,p, and the set of allp-by-p positive-definitesymmetric (Hermitian) matricesPp, which is the so-callednuisance parameter space. BothGn,p andPp may be repre-sented by sets of equivalence classes, known mathematically asquotient or homogeneous spaces. Though this representationis more abstract, it turns out to be very useful for obtainingclosed-form expressions of the necessary geometric objectsused in this paper. In fact, both the set of subspaces and theset of covariance matrices are what is known as reductivehomogeneous spaces, and therefore possess natural invariantconnections and metrics [10], [12], [24], [31], [37], [48].Quotient spaces are also the “proper” mathematical descriptionof these manifolds.

SMITH: COVARIANCE, SUBSPACE, INTRINSIC CRAMER-RAO BOUNDS 3
A Lie group G is a manifold with differentiable groupoperations. ForH ⊂ G a (closed) subgroup, the quotient‘G/H ’ denotes the set of equivalence classes [g] : g ∈ G ,where [g] = gH is the equivalence classgh1 ≡ gh2 for allh1, h2 ∈ H. For example, any positive-definite symmetricmatrix R has the Cholesky decompositionR = AAT, whereA ∈ Gl(p) (the general linear group) is an invertible matrixwith the unique polar decomposition [27]A = PQ, whereP ∈ Pp is a positive-definite symmetric matrix andQ ∈O(p) (the orthogonal Lie group) is an orthogonal matrix.Clearly R = PQQTP = P2, and the orthogonal partQof the polar decomposition is arbitrary in the specificationof R. Therefore, for any covariance matrixR ∈ Gl(p), thereis a corresponding equivalence class[R
12 ] = R
12 ·O(p) in
the quotient spaceGl(p)/O(p), where R12 is the unique
positive-definite symmetric square root ofR. Thus the setof covariance matricesPp may be equated with the quotientspaceGl(p)/O(p), allowing application of this space’s in-trinsic geometric structure to problems involving covariancematrices. In the Hermitian covariance matrix case, the correctidentification isPp
∼= Gl(p,C)/U(p), whereU(p) is the Liegroup of unitary matrices.
Another way of viewing the identification ofPp∼=
Gl(p)/O(p) is by the transitive group action [10], [31], [37]seen in Eq. (3) of the groupGl(p) acting onPp via the mapA : R 7→ ARAT. This action is almost effective (the matrices±I are the only ones that fix allR, ±I : R 7→= IRIT = R)and has the isotropy (invariance) subgroup ofO(p) at R = IbecauseQ : I 7→ QIQT = I for all orthogonal matricesQ.The only part of this group action that matters is the positive-definite symmetric part, becauseA : I 7→ AIAT = P2 =R. Thus the set of positive-definite symmetric (Hermitian)matrices may be viewed as the equivalence class of invertiblematrices multiplied on the right by an arbitrary orthogonal(unitary) matrix.
Though covariance matrices obviously have a unique matrixrepresentation, this is not true of subspaces, because forsubspaces, it is only the image (column span) of the matrixthat matters. Hence, quotient space methods are essential inthe description of problems involving subspaces. Edelmanet al. [22] provide a convenient computational framework forthe Grassmann manifoldGn,p involving its quotient spacestructure. Subspaces are represented by a single (nonunique)n-by-p matrix with orthonormal columns that itself representsthe entire equivalence class of matrices with the same col-umn span. Thus for the unknown matrixY, YTY = I,Y may be multiplied on the right by anyp-by-p orthog-onal matrix, i.e.,YQ for Q ∈ O(p), without affectingthe results. The Grassmann manifold is represented by thequotientO(n)/
(O(n− p)×O(p)
)because the set ofn-by-p
orthonormal matricesYQ : Q ∈ O(p)
is the same
equivalence class as the set ofn-by-n orthogonal matrices (Y Y⊥
)(Q0
0Q′
): Q ∈ O(p),Q′ ∈ O(n− p)
, where
Y⊥ is an arbitraryn-by-(n− p) matrix such thatYT⊥Y⊥ = I
and YTY⊥ = 0. Many other signal processing applicationsalso involve the Stiefel manifoldVn,p = O(n)/O(n− p) ofsubspace basis vectors or, equivalently, the set ofn-by-p matri-ces with orthonormal columns [22]. Another representation of
the Grassmann manifoldGn,p is the set of equivalence classesVn,p/O(p). Though the approach of this paper immediatelyapplies to the Stiefel manifold, it will not be considered here.
The reductive homogeneous space structure of bothPp
and Gn,p is exploited extensively in this paper, as are thecorresponding invariant affine connections and invariant met-rics [viz. Eqs. (65), (66), (119), and (122)]. Reductive homo-geneous spaces and their corresponding natural Riemannianmetrics appear frequently in signal processing and other ap-plications [1], [32], [41], [62], e.g., the Stiefel manifold in thesingular value and QR-decompositions, but their presence isnot widely acknowledged. A homogeneous spaceG/H is saidto be reductive [12], [31], [37] if there exists a decompositiong = m + h (direct sum) such thatAdH(m) def= hAh−1 : h ∈H, A ∈ m ⊂ m, whereg and h are the Lie algebras ofGandH, respectively. Given a bilinear form (metric) onm (e.g.,the trace ofAB, trAB, for symmetric matrices), there corre-sponds aG-invariant metric and a correspondingG-invariantaffine connection onG/H. This is said to be the natural metricon G/H, that essentially corresponds to a restriction of theKilling form on g in most applications. For the example ofthe covariance matrices,g = gl(p), the Lie algebra ofp-by-pmatrices [orgl(p,C)], h = so(p), the sub-Lie algebra of skew-symmetric matrices [or the skew-Hermitian matricesu(n)],andm = symmetric (Hermitian) matrices, so thatgl(p) =m + so(p) (direct sum). That is, anyp-by-p matrix A may beexpressed as the sum of its symmetric part1
2 (A + AT) andits skew-symmetric part12 (A−AT). The symmetric matricesareAdO(n)-invariant because for any symmetric matrixS andorthogonal matrixQ, AdQ(S) = QSQ−1 = QSQT, whichis also symmetric. Therefore,Pp
∼= Gl(p)/O(p) admits aGl(p)-invariant metric and connection corresponding to thebilinear formtrAB at R = I, specifically (up to an arbitraryscale factor),
gR(A,B) = trAR−1BR−1 (4)
at arbitrary R ∈ Pp. The reader may consult Edelmanet al. [22] for the details of the Grassmann manifoldGn,p
∼=O(n)/
(O(n− p)×O(p)
)for the subspace example.
Furthermore, the Grassmann manifoldGn,p and thepositive-definite symmetric matricesPp with their naturalmetrics are both Riemannian globally symmetric spaces [10],[24], [30], [37], though except for closed-form expressionsfor geodesics, parallel translation, and sectional curvature,the rich geometric properties arising from this symmetricspace structure are not used in this paper. As an aside forcompleteness,Gn,p is a compact irreducible symmetric spaceof type BD I, andPp
∼= Gl(p)/O(p) ∼= R × Sl(p)/SO(p)is a decomposable symmetric space, where the irreduciblenoncompact componentSl(n)/SO(p) is of type A I [30,chap. 10, secs. 2.3, 2.6; chap. 5, prop. 4.2; p. 238]. Elementsof Pp decompose naturally into the product of the determinantof the covariance matrix multiplied by a covariance matrixwith unity determinant, i.e.,R = (detR) · (R/detR).
C. Plan of the Paper
The paper’s body is organized into three major sectionsaddressing intrinsic estimation theory, covariance matrix esti-

4 TO APPEAR IN IEEE TRANS. SIGNAL PROCESSING
mation, and subspace and covariance estimation. In Section IIthe intrinsic Cramer-Rao bound and several of its propertiesare derived and explained using coordinate-free methods. InSection III, the well-known problem of covariance matrixestimation is analyzed using these intrinsic methods. A closed-form expression for the covariance matrix CRB is derived,and the bias and efficiency of the sample covariance matrixestimator is considered. It is shown that the SCM viewedintrinsically is a biased and inefficient estimator, and thatthe bias term reveals the degraded estimation accuracy thatis known to occur at low sample support. Intrinsic Cramer-Rao bounds for the subspace plus unknown covariance matrixestimation problem of Eq. (1) are computed in closed-formin Section IV and compared with a Monte Carlo simulation.The asymptotic efficiency of the standard subspace estimationapproach utilizing the singular value decomposition is alsoanalyzed.
II. T HE INTRINSIC CRAMER-RAO BOUND
An intrinsic version of the Cramer-Rao bound is developedin this section. There are abundant treatments of the CRB inits classical form [57], [75], its geometry [58], the case of aconstrained parameter space [28], [72], [77], and several gener-alizations of the CRB to arbitrary Riemannian manifolds [11],[33], [41], [50], [51], [65], [76] and statistical manifolds [5].It is necessary and desirable for the results in this paperto express the CRB using differential geometric languagethat is independent of any arbitrary coordinate system anda formula for Fisher information [25], [57], [75] that readilyyields CRB results for problems found in signal processing.Other intrinsic derivations of the Cramer-Rao bound usedifferent mathematical frameworks (comparison theorems ofRiemannian geometry, quantum mechanics) not immediatelyapplicable to signal processing and specifically to subspaceand covariance estimation theory.
Eight concepts from differential geometry are necessaryto define and efficiently compute the Cramer-Rao bound:a manifold, its tangent space, the differential of a func-tion, covariant differentiation, Riemannian metrics, geodesiccurves, sectional/Riemannian curvature, and the gradient of afunction. Working definitions of each of these concepts areprovided in footnotes; for complete, technical definitions, seeBoothby [10], Helgason [30], Kobayashi and Nomizu [37], orSpivak [66]. Also, Amari [3]–[6] has significantly extendedRao’s [53] original geometric treatment of statistics, and Mur-ray and Rice [46] provide a coordinate-free treatment of theseideas. Refer to the table on page 19 for a list of differentialgeometric objects and their more familiar counterparts inEuclideann-space,Rn. Higher order terms containing themanifold’s sectional (the higher dimensional generalizationof the 2-dimensional Gaussian curvature) and Riemanniancurvature [10], [12], [30], [33], [37], [50], [76], [77] also maketheir appearance in the intrinsic CRB; however, because theCRB is an asymptotic bound for small errors (high SNR andsample support), these terms are negligible for small errors.
A. The Fisher Information Metric
Let f(z|θ) be the probability density function (pdf) of avector-valued random variablez in the sample spaceRN ,given the parameterθ in the n-dimensional manifold1 M (nnot necessarily equal toN ). The CRB is a consequence of anatural metric structure defined on a statistical model, definedby the parameterized set of probability densities f(z|θ) :θ ∈M . Let
`(z|θ) = log f(z|θ) (5)
be the log-likelihood function, and letΘ andΩ be two tangentvectors2 on the parameter space. Define the Fisher informationmetric3 (FIM)
g(Θ,Ω) = E [d`(Θ)d`(Ω)], (6)
whered` is the differential4 of the log-likelihood function. Wemay retrench the dependence on explicit tangent vectors and
1A manifold is a space that “looks” likeRn locally, i.e., M may beparameterized byn coordinate functionsθ1, θ2, . . . ,θn that may be arbitrarilychosen up to obvious consistency conditions. (For example, positions on theglobe are mapped by a variety of2-dimensional coordinate systems: latitude-longitude, Mercator, and so forth.)
2 The tangent space of a manifold at a point is, nonrigorously, the set ofvectors tangent to that point; rigorously, it is necessary to define manifolds andtheir tangent vectors independently of their embedding in a higher dimension(e.g., as we typically view the2-sphere embedded in3-dimensional space).The tangent space is a vector space of the same dimension asM . This vectorspace atθ ∈ M is typically denoted byTθM . The dual space of linear mapsfrom TθM to R, called the cotangent space, is denotedT ∗θ M . We imaginetangent vectors to be column vectors and cotangent vectors to be row vectors.If we have a mappingφ : M → P from one manifold to another, then thereexists a natural linear mappingφ∗ : TθM → TφP from the tangent spaceat θ to the tangent space atφ(θ). If coordinates are fixed,φ∗ = ∂φ/∂θ,i.e., simply the Jacobian transformation. This linear map is called the push-forward, a notion that generalizes Taylor’s theorem:φ(θ + δθ) = φ(θ) +(∂φ/∂θ)δθ + h.o.t.= φ + δφ.
3A Riemannian metricg is defined by a nondegenerate inner product on themanifold’s tangent space, i.e.,g : TθM × TθM → R is a definite quadraticform at each point on the manifold. IfΩ is a tangent vector, then the square
length ofΩ is given by‖Ω‖2 = 〈Ω,Ω〉 def= g(Ω,Ω). Note that this inner
product depends on the location of the tangent vector. For the example ofthe sphere embedded in Euclidean space,Sn−1 = x ∈ Rn : xTx = 1 ,g(Ω,Ω) = ΩT(I−xxT)Ω for tangent vectorsΩ to the sphere atx ∈ Rn.For covariance matrices, the natural Riemannian metric is provided in Eq. (4);for subspaces, the natural metric is given in Eq. (118).
4The differential of a real-valued function: M → R on a manifold, calledd`, simply represents the standard directional derivative. Ifc(t) (t ∈ R) is acurve on the manifold, thenΩ = (d/dt)|t=0c(t) is a tangent vector atc(0),and the directional derivative of in directionΩ is given by
d`(Ω)def= (d/dt)|t=0`
`c(t)
´. (7)
Examining this definition with respect to a particular coordinate system,` may be viewed as a function(θ1, θ2, . . . , θn), the curve c(t) isviewed as
`c1(t), c2(t), . . . , cn(t)
´T, the tangent vector is given byΩ =(Ω1, Ω2, . . . , Ωn)T = (dc1/dt, dc2/dt, . . . , dcn/dt)T, and the directionalderivative is given by the equation
d`(Ω) =X
k
∂`
∂θkΩk. (8)
If we view Ω as an n-by-1 column vector, then d` =(∂`/∂θ1, ∂`/∂θ2, . . . , ∂`/∂θn) is a 1-by-n row vector. Furthermore,the basis vectors induced by these coordinates for the tangent spaceTθMare called(∂/∂θ1), (∂/∂θ2), . . . , (∂/∂θn) becaused`(∂/∂θk) = ∂`/∂θk.The dual basis vectors for the cotangent spaceT ∗θ M are called dθ1,dθ2, . . . , dθn becausedθi(∂/∂θj) = δi
j (Kronecker delta). Using thepush-forward concept for tangent spaces described in footnote 2,` : M → R,and`∗ : TθM → R, i.e.,d` = `∗, which is consistent with the interpretationof d` as a cotangent (row) vector.

SMITH: COVARIANCE, SUBSPACE, INTRINSIC CRAMER-RAO BOUNDS 5
express the FIM as
g = E [d`⊗ d`], (9)
where ‘⊗’ denotes the tensor product. The Fisher informationmatrix G (also abbreviated FIM) is defined with respectto a particular set of coordinate functions or parameters(θ1, θ2, . . . , θn) on M :
(G)ij = g
(∂
∂θi,∂
∂θj
)= E
[∂`
∂θi
∂`
∂θj
]. (10)
Refer to footnote 4 and the table on page 19 for an explanationof the notation ‘∂/∂θi’ for tangent vectors.
Of course, the Fisher information metric is invariant to thechange of coordinatesφ = φ(θ), i.e.,φi = φi(θ1, θ2, . . . , θn)(i = 1, . . . , n), because the Fisher information matrix trans-forms contravariantly:
Gθ = JTφGφJφ, (11)
whereGθ and Gφ are the Fisher information matrices withrespect to the coordinates specified by their subscripts, and(Jφ)i
j = ∂φi/∂θj is the Jacobian of the change of variables.Because the JacobianJφ determines how coordinate trans-formations affect accuracy bounds, it is sometimes called asensitivity matrix [43], [58].
Though the definition of the FIM employing first derivativesgiven by Eq. (9) is sufficient for computing this metric, inmany applications (such as the ones considered in this paper)complicated derivations involving cross terms are oftentimesencountered. (It can be helpful to apply multivariate analysisto the resulting expressions. See, for example, Exercise 2.5 ofFang and Zhang [23]). Derivations of Cramer-Rao bounds aretypically much simpler if the Fisher information is expressedusing the second derivatives5 of the log-likelihood function.The following theorem provides this convenience for an arbi-trary choice of affine connection∇, which allows a great dealof flexibility (∇ is not the gradient operator; see footnotes 5and 8). The FIM is independent of the arbitrary metric (andits induced Levi-Civita connection) chosen to define the root-mean-square error (RMSE) on the parameter space.
5Differentiating real-valued functions defined on manifolds is straight-forward because we may subtract the value of the function at one pointon the manifold from its value at a different point. Differentiating firstderivatives again or tangent vectors, however, is not well defined (withoutspecifying additional information) because a vector tangent at one pointis not (necessarily) tangent at another: subtraction between two differentvector spaces is not intrinsically defined. The additional structure requiredto differentiate vectors is called the affine connection∇, so-called because itallows one to “connect” different tangent spaces and compare objects definedseparately at each point. [This isnot the gradient operator; see Eq. (47) infootnote 8.] The covariant differential of a function` along tangent vectorΩ,written ∇`(Ω) or ∇Ω`, is simply d`(Ω). In a particular coordinate system,the i-th component of∇` is (∂`/∂θi). The ij-th component of the secondcovariant differential∇2`, the generalization of the Hessian, is given by
(∇2`)ij =∂2`
∂θi∂θj−
Xk
Γkij
∂`
∂θk, (12)
where
Γkij =
1
2
Xl
gkl
„∂gil
∂xj+
∂gjl
∂xi−
∂gij
∂xl
«(13)
Theorem 1 Let f(z|θ) be a family of pdfs parameterized byθ ∈ M , ` = log f be the log-likelihood function, andg =E [d` ⊗ d`] be the Fisher information metric. For any affineconnection∇ defined onM ,
g = −E [∇2`]. (16)
Proof: The proof is a straightforward application of thelemma: E [d`] = 0, which follows immediately from dif-ferentiating the identity
∫f(z|θ) dz = 1 with respect toθ
and observing thatdf = f d`. Applying this lemma to∇2`, expressed in arbitrary coordinates as in Eq. (12),it is seen that
∫(∇2`)f dz =
∫(∂2`/∂θi∂θj)f dz −∑
k Γkij
∫(∂`/∂θk)f dz = −
∫(∂`/∂θi)(∂`/∂θj)f dz, the last
equality following from integration by parts, as in classicalCramer-Rao analysis.
Theorem 1 allows us to compute the Fisher information onan arbitrary manifold using precisely the same approach as isdone in classical Cramer-Rao analysis. To see why this is so,consider the following expression for the Hessian of the log-likelihood function defined on an arbitrary manifold endowedwith the affine structure∇:
(∇2`)θ0(Ω,Ω) =d2
dt2
∣∣∣∣t=0
`(θ(t)
), (17)
whereθ(t) is a geodesic6 emanating fromθ0 in the directionΩ. Evaluatingθ(t) for smallt [12], [66, vol. 2, chap. 4, props.
are the Christoffel symbols (of the second kind) of the connection definedby ∇∂/∂θi (∂/∂θj) =
Pk Γk
ij(∂/∂θk), or defined by the equation for
geodesicsθk +P
i,j Γkij θiθj = 0 in footnote 6. It is sometimes more
convenient to work with Christoffel symbols of the first kind, denotedΓij,k,where Γk
ij =P
l gklΓij,l, i.e., theΓij,l are given by the expression inEq. (13) without thegkl term. For torsion-free connections (the typical casefor applications), the Christoffel symbols possess the symmetriesΓk
ij = Γkji
and Γik,j + Γjk,i = 0. It is oftentimes preferable to use matrix notationΓ(θ, θ) to express the quadratic terms in the geodesic equation [22]. For asphere embedded in Euclidean space, the Christoffel symbols are given bythe coefficients of the quadratic formΓ(Ω1,Ω2) = x·(ΩT
1 Ω2) for tangentvectorsΩ1 andΩ2 to the sphere atx in Rn [22] [cf. Eq. (122)]. Theij-thcomponent of the covariant differential of a vector fieldΩ(θ) ∈ TθM is
(∇Ω)ij =
∂Ωi
∂θj+
Xk
ΓijkΩk. (14)
Classical index notation is used here and throughout the paper (see, forexample, Spivak [66] or McCullagh [42] for a description). A useful wayto compute the covariant derivative is∇ΘΩ = Ω(0) + Γ
`Ω(0),Θ
´for
the vector fieldΩ(t) = Ω(expθ tΘ) (the “expθ” notation for geodesics isexplained in footnote 6).
In general, the covariant derivative of an arbitrary tensorT on M alongthe tangent vectorΘ is given by the limit
∇ΘT = limt→0
τ−1t T (t)− T (0)
t, (15)
whereT (t) denotes the tensor at the pointexpθ(tΘ) andτt denotes paralleltranslation fromθ to θ(t) = expθ(tΘ) [10], [30], [37], [66]. Covariantdifferentiation generalizes the concept of the directional derivative ofTalongΘ and encodes all intrinsic notions of curvature on the manifold [66,vol. 2, chaps. 4–8]. The parallel translation of a tensor fieldB(t) = τtB0
satisfies the differential equation∇θB = 0.6A geodesic curveθ(t) on a manifold is any curve that satisfies the
differential equation
∇θ θ = θk +Xi,j
Γkij θiθj = 0; θ(0) = θ0; θ(0) = Ω. (18)

6 TO APPEAR IN IEEE TRANS. SIGNAL PROCESSING
1 and 6] yields
θ(t) = θ0 + tΩ +O(t3). (19)
This equation should be interpreted to hold for normal coor-dinates (in the sense of footnote 6)θ = (θ1, θ2, . . . , θn) ∈ Rn
on M . Applying Eqs. (17) and (19) to compute the Fisherinformation metric, it is immediately seen that for normalcoordinatesθ = (θ1, θ2, . . . , θn) ∈ Rn,(
−E [∇2`])ij
= −E∂2`
∂θi∂θj, (20)
where the second derivatives of the right hand side of Eq. (20)represent the ordinary Hessian matrix of`(θ), interpreted tobe a scalar function defined onRn. As with any bilinear form,the off-diagonal terms of the FIM may be computed using thestandard process of polarization:
g(A,B) = 14
(g(A + B,A + B)− g(A−B,A−B)
). (21)
Compare this FIM approach to other intrinsic treatments ofCramer-Rao bounds that employ the exponential map explic-itly [33], [41], [49], [50].
Thus, Fisher information does not depend on the choiceof any particular coordinates or any underlying Riemannianmetric (or affine connection). We should expect nothing lessthan this result, as it is true of classical estimation bounds.For example, discounting a scaling factor, measurements infeet versus meters do not affect range estimation bounds.
B. Intrinsic Estimation Theory
Let f(z|θ) be a parameterized pdf, whereθ takes on valuesin the manifoldM . An estimatorθ(z) of θ is a mappingfrom the space of random variables toM . Oftentimes thisspace of random variables is a product space comprisingmany snapshots taken from some underlying distribution.Because addition and subtraction are not defined betweenpoints on arbitrary manifolds, an affine connection∇ on M(see footnotes 5 and 6) must be assumed to make sense of theconcept of the mean value ofθ on M [49]. Associated withthis connection is the exponential mapexpθ : TθM → Mfrom the tangent space at any pointθ to points onM (i.e.,geodesics) and its inverseexp−1
θ : M → TθM . Looking ahead,the notation “exp” and “exp−1” is explained by the form ofdistances and geodesics on the space of covariance matricesPn and the Grassmann manifoldGn,p provided in Eqs. (65),
If ∇ is a Riemannian connection, i.e.,∇g ≡ 0 for the arbitrary Rieman-nian metricg, Eq. (18) yields length minimizing curves. The mapΩ 7→θ(t) = expθ0
(Ωt) is called the exponential map and provides a naturaldiffeomorphism between the tangent space atθ0 and a neighborhood ofθ0
on the manifold. Looking ahead, the notation “exp” explains the appearance ofmatrix exponentials in the equations for geodesics on the space of covariancematricesPn and the Grassmann manifoldGn,p given in Eqs. (67) and (120).The geodesicθ(t) is said to emanate fromθ0 in direction Ω. By theexponential map, any arbitrary choice of basis of the tangent space atθ0 yieldsa set of coordinates onM nearθ0; the coordinates are callednormal [30],[37], [66]. One important fact that will be used in Sections III and IV todetermine covariance and subspace estimation accuracies is that the lengthof the geodesic curve fromθ0 to θ(t) is |t|·‖Ω‖. For the sphere embeddedin Euclidean space, geodesics are great circles, as can be seen by verifyingthat the pathsx(t) = x cos σt + Ω sin σt [xTΩ = 0, xTx = ΩTΩ = 1;cf. Eq. (120)] satisfy the differential equationx + Γ(x, x) = 0, where theChristoffel symbolΓ for the sphere is given in footnote 5.
exp q–1q
‹
q
‹
M
T Mq
qb(q)
[q]
‹
qE
Fig. 1. Intrinsic estimation on a manifold. The estimatorθ(z) of theparameterθ is shown, wherez is taken from the family of pdfsf(z|θ) whoseparameter set is the manifoldM . The exponential map “expθ” equates pointson the manifold with points in the tangent spaceTθM at θ via geodesics(see footnotes 5 and 6). This structure is necessary to define the expectedvalue of θ because addition and subtraction are not well defined betweenarbitrary points on a manifold [see Eq. (22)]. The bias vector field [Eq. (23)]is defined byb(θ) = exp−1
θ Eθ [θ] = E [exp−1θ θ] and therefore depends
upon the geodesics chosen onM .
q
‹
M
q
exp t Wqt W
XX – t W – t Q(X )W
Fig. 2. The failure of vector addition in Riemannian manifolds. Sectionaland Riemannian curvature terms (see footnote 7) appearing in the CRB arisefrom the expression∇exp−1
θ θ, which contains a quadratic formQ(X)
in X = exp−1θ θ. This quadratic form is directly expressible in terms of
the Riemannian curvature tensor and the manifold’s sectional curvatures [66,vol. 2, chap. 4]. These terms are negligible for the small errors and biases,the domain of interest for CRBs, i.e.,d(θ, θ) (max |KM |)−1/2, whereKM is the manifold’s sectional curvature.
(67), (69), (119), and (120). IfM is connected and complete,the function expθ is onto [30], but its inverseexp−1
θ mayhave multiple values (e.g., multiple windings for great-circlegeodesics on the sphere). Typically, the tangent vector ofshortest length may be chosen. In the case of conjugate pointsto θ [12], [30], [37] (whereexpθ is singular, e.g., antipodeson the sphere), an arbitrary tangent vector may be specified;however, this case is of little practical concern because theset of such points has measure zero and the CRB itself is anasymptotic bound used for small errors. The manifoldPn hasnon-positive curvature (see Eq. (28) in footnote 7); therefore,it has no conjugate points [37, vol. 2, chap. 8, sec. 8], andin fact exp−1 is uniquely defined by the unique logarithmof positive-definite matrices in this case. For the Grassmannmanifold Gn,p, exp−1 is uniquely defined by the principalvalue of the arccosine function.
Definition 1 Given an estimatorθ of θ ∈M , theexpectationof the estimatorθ with respect toθ, denotedEθ[θ] ∈M , and

SMITH: COVARIANCE, SUBSPACE, INTRINSIC CRAMER-RAO BOUNDS 7
the bias vector fieldb(θ) ∈ TθM of θ are defined as
Eθ[θ] def= expθ E [exp−1θ θ] = expθ
∫(exp−1
θ θ)f(z|θ) dz,
(22)
b(θ) def= exp−1θ Eθ[θ] = E [exp−1
θ θ]. (23)
Figure 1 illustrates these definitions. Note that, unlike thestandard expectation operatorE [·], Eθ[·] is not (necessarily)linear as it does not operate on linear spaces. These defini-tions are independent of arbitrary coordinates(θ1, θ2, . . . , θn)on M , but do depend on the specific choice of affine con-nection∇, just as the bias vector inRn depends upon vectoraddition. In fact, because for every connection∇ there is aunique torsion-free connection∇ with the same geodesics [66,vol. 2, chap. 6, cor. 17], the bias vector really depends uponthe choice of geodesics onM .
Definition 2 The estimatorθ is said to beunbiasedif b ≡ 0(the zero vector field) so thatEθ[θ] = θ. If ∇b ≡ 0, thebias b(θ) is said to beparallel.
In the ordinary case of Euclideann-space (i.e.,M = Rn),the exponential map and its inverse are simply vector addition,i.e., expθ
(b(θ)
)= θ + b(θ) and exp−1
θ θ = θ − θ. Parallelbias vectors are constant in Euclidean space because∇b =∂b/∂x ≡ 0. The proof of the CRB in Euclidean spacesrelies upon that fact that(∂/∂θ)(θ − θ) = −I. However, forarbitrary Riemannian manifolds,∇ exp−1
θ θ = −I plus secondorder and higher terms involving the manifolds’s sectional andRiemannian curvatures.7 The following lemma quantifies these
7The sectional curvature is Riemann’s higher dimensional generalization ofthe Gaussian curvature encountered in the study of2-dimensional surfaces.Given a circle of radiusr in a 2-dimensional subspaceH of the tangent spaceTθM , let A0(r) = πr2 be the area of this circle, and letA(r) be the area ofthe corresponding “circle” in the manifold mapped using the functionexpθ .Then the sectional curvature ofH is defined [30] to be
K(H) = limr→0
12A0(r)−A(r)
r2A0(r). (24)
We shall also writeKM to specify the manifold. For the example of the unitsphereSn−1, A(r) = 2π(1− cos r), andKSn−1 ≡ 1, i.e., the unit sphereis a space of constant curvature unity. Eq. (24) implies that the area in themanifold is smaller for planes with positive sectional curvature, i.e., geodesicstend to coalesce, and conversely that the area in the manifold is larger forplanes with negative sectional curvature, i.e., geodesics tend to diverge fromeach other.
Given tangent vectorsX and Y and the vector fieldZ, the Riemanniancurvature tensor is defined to be
R(X, Y )Z = ∇X∇Y Z −∇Y ∇XZ −∇[X,Y ]Z, (25)
where [X, Y ] = XY − YX ∈ TθM is the Lie bracket. The RiemanniancurvatureR(X, Y )Z measures the amount by which the vectorZ is alteredas it is parallel translated around the “parallelogram” in the manifold definedby X andY [30, chap. 1, ex. E.2]:R(X, Y )Z = limt→0
`Z−Z(t)
´/t2,
whereZ(t) is the parallel translation ofZ. Remarkably, sectional curvatureand Riemannian curvature are equivalent: then(n−1)/2 sectional curvaturescompletely determine the Riemannian curvature tensor, and vice-versa. Therelationship between the two is
K(X ∧ Y ) =〈R(X, Y )Y , X〉
‖X ∧ Y ‖2, (26)
whereK(X ∧ Y ) is the sectional curvature of the subspace spanned byXand Y , ‖X ∧ Y ‖2 = ‖X‖2‖Y ‖2 sin2 α is the square area of theparallelogram formed byX andY , andα is the angle between these vectors.Figure 2 illustrates how curvature causes simple vector addition to fail.
nonlinear terms, which are negligible for small errors (smalldistancesd(θ, expθ b) betweenθ andexpθ b) and small biases(small vector norm‖b‖), though these higher order terms doappear in the intrinsic Cramer-Rao bound.
Lemma 1 Let f(z|θ) be a family of pdfs parameterized byθ ∈ M , ` = log f be the log-likelihood function,g be anarbitrary Riemannian metric (not necessarily the FIM),∇ bean affine connection onM corresponding tog, and, for anyestimatorθ of θ with bias vector fieldb(θ), let the matrixCdenote the covariance ofX − b(θ), X = exp−1
θ θ, all withrespect to the arbitrary coordinates(θ1, θ2, . . . , θn) near θand corresponding tangent vectorsEi = ∂/∂θi, i = 1, . . . ,n.(1) Then
E [(exp−1θ θ − b)d`] = I− 1
3‖b‖2K(b)− 1
3Rm(C) +∇b,(31)
where the term− 13‖b‖
2K(b) − 13Rm(C) is defined by the
expression
−E [∇exp−1θ θ] = I− 1
3‖b‖2K(b)− 1
3Rm(C). (32)
(2) For sufficiently small bias norm‖b‖, the ij-th element ofK(b) is
(K(b)
)ij
=
sin2 αi·K(b ∧Ei) +O(‖b‖3), if i = j;[sin2 α′ij ·K
(b ∧ (Ei + Ej)
)− sin2 α′′ij ·K
(b ∧ (Ei −Ej)
)]+O(‖b‖3),
if i 6= j,
(33)where K(H) denotes the sectional curvature of the2-dimensional subspaceH ⊂ TθM , and αi, α′ij , and α′′ij are
There are relatively simple formulas [12], [13], [30] for the Riemanniancurvature tensor in the case of homogeneous spaces encountered in signalprocessing applications. Specifically, the Lie groupG = Gl(n, C) isnoncompact and its Lie algebrag = gl(n, C) admits a decompositiong = m + h [direct sum,m = Hermitian matrices,h = u(n)], such that
[m, m] ⊂ h, [m, h] ⊂ m, [h, h] ⊂ h. (27)
The sectional curvature of the symmetric homogeneous spacePn∼=
Gl(n, C)/ U(n) is given by [13, prop. 3.39], [30, chap. 5, sec. 3]
K(X∧Y ) = −‖[ 12X, 1
2Y ]‖2h = − 1
4‖[X, Y ]‖2 = 1
4tr([X, Y ])2, (28)
where X and Y are orthonormal Hermitian matrices and[X, Y ] =XY − YX ∈ u(n) is the Lie bracket. (The scalings1
2and 1
4arise from
the fact that the matrixR ∈ Pn corresponds to the equivalence classR12 ·H
in G/H.) Note thatPp has nonpositive curvature everywhere. Similarly forthe Grassmann manifold, the Lie groupO(n) (U(n) in the complex case) iscompact, and its Lie algebra admits a comparable decomposition (see Edelmanet al. [22, sec. 2.3.2] for application-specific details). The sectional curvatureof the Grassmann manifoldGn,p
∼= O(n)/`O(n− p)×O(p)
´equals
KGn,p (X ∧ Y ) = ‖[X, Y ]‖2h = − 12
tr([X, Y ])2, (29)
whereX andY are skew-symmetric matrices of the form0A
−AT
0
´, and
A is an (n− p)-by-p matrix. (The signs in Eqs. (28) and (29) are correctbecause for an arbitrary skew-symmetric matrixΩ, ‖Ω‖2 = trΩTΩ =− trΩ2.) The sectional curvature ofGn,p is nonnegative everywhere. For thecasesp = 1 or p = n− 1, check that Eq. (29) is equivalent to the constantcurvatureKSn−1 ≡ 1 for the sphereSn−1 given above. To bound the termsin the covariance and subspace CRBs corresponding with these curvatures,we note that
max |KPn | =14
and max KGn,p = 1. (30)

8 TO APPEAR IN IEEE TRANS. SIGNAL PROCESSING
the angles between the tangent vectorb andEi, Ei +Ej , andEi −Ej , respectively.(3) For sufficiently small covariance normλmax(C), thematrix Rm(C) is given by the quadratic form
〈Rm(C)Ω,Ω〉 = E[〈R(X − b,Ω)Ω,X − b〉
], (34)
whereR(X,Y )Z is the Riemannian curvature tensor. Fur-thermore, the matricesK(b) andRm(C) are symmetric, andRm(C) depends linearly onC.
Proof: First take the covariant derivative of the identity∫(exp−1
θ θ − b)f(z|θ) dz = 0 (the zero vector field). To dif-ferentiate the argument inside the integral, recall that foran arbitrary vector fieldΩ, ∇(fΩ) = df ·Ω + f ·(∇Ω).The integral of the first part of this sum is simply theleft-hand side of Eq. (31); therefore,E [(exp−1
θ θ − b)d`] =−E [∇(exp−1
θ θ − b)] = −E [∇exp−1θ θ] + ∇b. This estab-
lishes part (1). The remainder of the proof is a straightforwardcomputation using normal coordinates (see footnote 6) and isillustrated in Figure 2. We will compute∇Ω exp−1
θ θ, Ω ∈TθM , using Eq. (15) from footnote 5. Define the tangentvectorsX = exp−1
θ θ ∈ TθM and Y ∈ Texpθ tΩM by theequations
θ = expθ X = expexpθ tΩ Y . (35)
Assume that theEi are an orthonormal basis ofTθM . Ex-pressing all of the quantities in terms of the normal coordinatesexpθ
(∑i θ
iEi
), the geodesic fromθ to θ is simply the curve
θ = θi(t) = tXi, whereX =∑
iXiEi. The geodesic curve
from expθ tΩ to θ satisfies Eq. (18) in footnote 6 subject tothe boundary condition specified in Eq. (35). Using Riemann’soriginal local analysis of curvature, the metric is expressed asthe Taylor series [66, vol. 2, chap. 4]
gij = δij +∑kl
aij,klθkθl + · · · , (36)
where aij,kl = 12 (∂2gij/∂θ
k∂θl), which possess the sym-metries aij,kl = aji,kl = aij,lk = akl,ij and aij,kl +aik,jl + ail,jk = 0. Applying Eq. (13) in footnote 5 gives theChristoffel symbols (of the first kind)Γij,k = −2
∑l aij,klθ
l.Solving the geodesic equation forY to second order inXyields
Y = X − tΩ− tQ(X)Ω, (37)
whereQ(X) =∑
kl aij,klXkX l denotes the quadratic form
in Eq. (36). The parallel translation ofY along the geodesicexpθ tΩ equalsY (t) = Y +O(t2). Therefore,
−∇Ω exp−1θ θ = Ω + Q(X)Ω +O
(‖X‖3
)(38)
(also see Karcher [36, app. C3]). Riemann’s quadratic formQ(X,Y ) = Y TQ(X)Y =
∑ij,kl aij,klX
kX lY iY j simplyequals− 1
3‖X ∧ Y ‖2K(X ∧ Y ) = 〈R(X,Y )Y ,X〉, whereK(X ∧ Y ) is the sectional curvature of the subspace spannedby X andY , ‖X ∧ Y ‖2 = ‖X‖2‖Y ‖2 sin2 α is the squarearea of the parallelogram formed byX andY , α is the anglebetween these vectors, andR(X,Y )Z is the Riemannian
curvature tensor (see footnote 7). Taking the inner productof Eq. (38) withΩ,
〈−∇Ω exp−1θ θ,Ω〉
= ‖Ω‖2 + Q(X,Ω) +O(‖X‖3
),
= ‖Ω‖2 + Q(b + (X − b),Ω
)+O
(‖X‖3
),
= ‖Ω‖2 + Q(b,Ω) + Q(X − b,Ω)
+ 2ΩT(∑
kl aij,kl(b)k(X − b)l)Ω +O
(‖X‖3
),
= ‖Ω‖2 − 13‖b‖
2‖Ω‖2 sin2 α·K(b ∧Ω)− 1
3 〈R(X − b,Ω)Ω,X − b〉+ 2ΩT
(∑kl aij,kl(b)k(X − b)l
)Ω +O
(‖X‖3
), (39)
whereα is the angle betweenΩ and b. Ignoring the higherorder termsO
(‖X‖3
), the expectation of Eq. (39) equals
E[〈−∇Ω exp−1
θ θ,Ω〉]
= ‖Ω‖2 − 13‖b‖
2‖Ω‖2 sin2 α·K(b ∧Ω)− 1
3 E[〈R(X − b,Ω)Ω,X − b〉
]= ‖Ω‖2 − 1
3‖b‖2‖Ω‖2 sin2 α·K(b ∧Ω)− 1
3Rm(C).(40)
Applying polarization [Eq. (21)] to Eq. (40) using the or-thonormal basis vectorsE1, . . . , En establishes parts (2)and (3), and shows thatK(b) and Rm(C) are symmetric.Using normal coordinates, theij-th element of the ma-trix Rm(C) is seen to be(
Rm(C))ij
= −3∑
kl aij,kl(C)kl, (41)
which depends linearly on the covariance matrixC.
As with Gaussian curvature, the units of the sectional andRiemannian curvaturesK and R(X,Y ) are the reciprocalof square distance; therefore, the sectional curvature termsin Lemma 1 are negligible for small errorsd(θ, expθ b) andbias norm‖b‖ much less than(max |K|)−1/2, i.e., errors andbiases less than the reciprocal square root of the maximalsectional curvature. For example, the unit sphere has constantsectional curvature of unity; therefore, the matricesK(b)andRm(C) may be neglected in this case for errors and biasesmuch smaller than1 radian.
The intrinsic generalization of the Cramer-Rao lower boundis:
Theorem 2 (Cramer-Rao) Let f(z|θ) be a family of pdfsparameterized byθ ∈ M , let ` = log f be the log-likelihoodfunction,g = E [d`⊗d`] be the Fisher information metric, and∇ be an affine connection onM . (1) For any estimatorθ of θwith bias vector fieldb(θ), the covariance matrix ofX−b(θ),X = exp−1
θ θ, satisfies the matrix inequality
C + 13
(Rm(C)G−1MT
b + MbG−1Rm(C))
− 19Rm(C)G−1Rm(C) ≥ MbG−1MT
b , (42)
where C = Cov(X − b) def= E [(X − b)(X − b)T] is thecovariance matrix,
Mb = I− 13‖b‖2K(b) +∇b, (43)

SMITH: COVARIANCE, SUBSPACE, INTRINSIC CRAMER-RAO BOUNDS 9
(G)ij = g(∂/∂θi, ∂/∂θj) is the Fisher information matrix,Iis the identity matrix,(∇b)i
j = (∂bi/∂θj)+∑
k Γijkbk is the
covariant differential ofb(θ), Γijk are the Christoffel symbols,
and the matricesK(b) andRm(C) representing sectional andRiemannian curvature terms are defined in Lemma 1, all withrespect to the arbitrary coordinates(θ1, θ2, . . . , θn) near θ.(2) For λmax(MbG−1MT
b ) sufficiently small relativeto (max |KM |)−1, C satisfies the matrix inequality
C ≥ MbG−1MTb − 1
3
(Rm(MbG−1MT
b )G−1MTb
+MbG−1Rm(MbG−1MTb )T)+O
(λmax(MbG−1MT
b )3).
(44)
(3) Neglecting the sectional and Riemannian curvature termsK(b) and Rm(C) at small errors and biases,C satisfies
C ≥ (I +∇b)G−1(I +∇b)T. (45)
The reader may substitute “θ − θ” for the expression“exp−1
θ θ,” interpreting it as the component-by-componentdifference for some set of coordinates. In the trivial caseM = Rn, the proof of Theorem 2 below is equivalent toasserting that the covariance matrix of the zero-mean randomvector
v = θ − θ − b(θ)−(I + (∂b/∂θ)
)(gradθ `) (46)
is positive semi-definite, wheregradθ ` is the gradient8 of `with respect to the FIMG. Readers unfamiliar with technical-ities in the proof below are encouraged to prove the theoremin Euclidean space using the fact thatE [vvT] ≥ 0. As usual,the matrix inequalityA ≥ B is said to hold for positive semi-definite matricesA andB if A−B ≥ 0, i.e.,A−B is positivesemi-definite, oruT(A−B)u ≥ 0 for all vectorsu.
8The gradient of a function is defined to be the unique tangent vectorgrad ` ∈ TθM such thatg(grad `,Ω) = d`(Ω) for all tangent vectorsΩ.With respect to particular coordinates,
grad ` = G−1d`T, (47)
i.e., thei-th element ofgrad ` is (grad `)i =P
j gij(∂`/∂θj), wheregij
is the ij-th element of the matrixG−1. Multiplication of any tensor bygij
(summation implied) is called “raising an index,” e.g., ifAj = ∂`/∂θj are thecoefficients of the differentiald`, thenAi =
Pj gijAj are the coefficients
of grad `. The presence ofG−1 in the gradient accounts for its appearancein the CRB.
The process of inverting a Riemannian metric is clearly important forcomputing the CRB. Given the metricg : TθM × TθM → R, there is acorresponding tensorg−1 : T ∗θ M × T ∗θ M → R naturally defined by theequation
g−1(ω, ω) = g(Ω,Ω) (48)
for all tangent vectorsΩ, where the cotangent vectorω ∈ T ∗θ M is definedby the equationg(Ω, X) = ω(X) for all X ∈ TθM (see footnotes 2 and 4for the definition of the cotangent spaceT ∗θ M ). The coefficients of the metricgij and the inverse metricgij with respect to a specific basis are computedas follows. Given an arbitrary basis(∂/∂θ1), (∂/∂θ2), . . . , (∂/∂θn) of thetangent spaceTθM and the corresponding dual basisdθ1, dθ2, . . . , dθn ofthe cotangent spaceT ∗θ M such thatdθi(∂/∂θj) = δi
j (Kronecker delta),we have
gij = g(∂/∂θi, ∂/∂θj), (49)
gij = g−1(dθi, dθj). (50)
ThenP
k,l gikgjlgkl = gij (tautologically, raising both indices ofgij ), andthe coefficientsgij of the inverse metric express the Cramer-Rao bound withrespect to this basis.
Proof: The proof is a direct application of Lemma 1 to thecomputation of the covariance of the random tangent vector
v = exp−1θ θ − b(θ)−
(Mb − 1
3Rm(C))(gradθ `), (51)
wheregradθ ` is the gradient of with respect to the FIMG(see footnote 8). Denotingexp−1
θ θ by X, the covariance ofvis given by
E [vvT] = E[(
X − b−(Mb − 1
3Rm(C))G−1d`T
)×(X − b−
(Mb − 1
3Rm(C))G−1d`T
)T],
= Cov(X − b)
−(Mb − 1
3Rm(C))G−1 E
[d`T(X − b)T
]− E
[(X − b)d`
]G−1
(Mb − 1
3Rm(C))T
+(Mb − 1
3Rm(C))G−1 E [d`Td`]
×G−1(Mb − 1
3Rm(C))T,
= C−(Mb − 1
3Rm(C))G−1
(Mb − 1
3Rm(C))T
−(Mb − 1
3Rm(C))G−1
(Mb − 1
3Rm(C))T
+(Mb − 1
3Rm(C))G−1
(Mb − 1
3Rm(C))T,
= C−(Mb − 1
3Rm(C))G−1
(Mb − 1
3Rm(C))T,
= C−MbG−1MTb
+ 13
(Rm(C)G−1MT
b + MbG−1Rm(C))
− 19Rm(C)G−1Rm(C). (52)
The mean ofv vanishes,E [v] = 0, and the covariance ofv,E [vvT], is positive semi-definite, which establishes the firstpart of the theorem. ExpandingC = MbG−1MT
b + ∆1 + · · ·into a Taylor series about the zero matrix0 and computingthe first-order term∆1 = − 1
3
(Rm(MbG−1MT
b )G−1MTb +
MbG−1Rm(MbG−1MTb ))
establishes the second part. Thethird part is trivial.
For applications, the intrinsic FIM and CRB are computedas described in the box on page 10. The significance ofthe sectional and Riemannian curvature terms is an openquestion that depends upon the specific application; however,as noted earlier, these terms become negligible for small errorsand biases. Assuming that the inverse FIMG−1 has unitsof (beamwidth)2/SNR for some beamwidth, as is typical,dimensional analysis of Eq. (44) shows that the Riemanniancurvature appears in theSNR−2 term of the CRB.
Several corollaries follow immediately from Theorem 2.Note that the tensor productv⊗v of a tangent vector with itselfis equivalent to the outer productvvT given a particular choiceof coordinates [cf. Eqs. (9) and (10) for cotangent vectors].
Corollary 1 The second-order moment ofexp−1θ θ, given by
E[(exp−1
θ θ)⊗ (exp−1θ θ)
]= Cov
(exp−1
θ θ − b(θ))
+ b(θ)⊗ b(θ) (53)
(viewed as a matrix with respect to given coordinates), satisfiesthe matrix inequality
E[(exp−1
θ θ)(exp−1θ θ)T
]≥ MbG−1MT
b + b(θ)b(θ)T
− 13
(Rm(MbG−1MT
b )G−1MTb+MbG−1Rm(MbG−1MT
b ))(54)

10 TO APPEAR IN IEEE TRANS. SIGNAL PROCESSING
COMPUTATION OF THE INTRINSIC FIM AND CRB
• Given the log-likelihood function (z|θ) with θ ∈M andΩ ∈ TθM , compute the Fisher informationmetric (FIM) using Theorem 1:
gfim(Ω,Ω) = −E[(d2/dt2)|t=0`(z|θ + tΩ)
].
This is a quadratic form inΩ.
• Polarize the FIM using the standard formula forquadratic forms [Eq. (21)]:
gfim(Ω1,Ω2) = 14
(gfim(Ω1 + Ω2,Ω1 + Ω2)
− gfim(Ω1 −Ω2,Ω1 −Ω2)).
• Select the desired basisΩ1, Ω2, . . . , Ωn for TθMand compute the elementsgij of the n-by-n Fisherinformation matrixG with respect to this basis asin Eq. (10):
gij = gfim(Ωi,Ωj).
Cramer-Rao bounds derived for this FIM representaccuracy bounds on the coefficientsAi, i = 1, . . . ,n,in the vector decompositionΩ =
∑iA
iΩi. IfM = Rn, this step is equivalent to assigningthe matrix elementsgij = eT
i Gej , where ei =(0, . . . , 0, 1, 0, . . . , 0)T is the i-th standard basis el-ement ofRn.
• To compute the unbiased CRB, invert the FIM usingone of the following methods:
Invert the matrixG directly.
Compute the (inverse) quadratic formg−1fim : T ∗θM × T ∗θM → R using Eq. (48) of
footnote 8 and the dual basisΩ∗1, Ω∗
2, . . . , Ω∗n
for the cotangent spaceT ∗θM such thatΩ∗
i (Ωj) = δij , then computegij = (G−1)ij
directly using Eq. (50):
gij = g−1fim(Ω∗
i ,Ω∗j ).
for sufficiently small‖b‖2 and λmax(MbG−1MTb ) relative
to (max |KM |)−1. Neglecting the sectional and Riemanniancurvature termsK(b) andRm(C) at small errors and biases,
E[(exp−1
θ θ)(exp−1θ θ)T
]≥ (I +∇b)G−1(I +∇b)T + b(θ)b(θ)T. (55)
Corollary 2 Assume thatθ is an unbiased estimator, i.e.,b(θ) ≡ 0 (the zero vector field). Then the covariance of theestimation errorexp−1
θ θ satisfies the inequality
Cov(exp−1θ θ) ≥ G−1− 1
3
(Rm(G−1)G−1+G−1Rm(G−1)
).
(56)
Neglecting the Riemannian curvature termsRm(C) at smallerrors, the estimation error satisfies
Cov(exp−1θ θ) ≥ G−1. (57)
Corollary 3 (Efficiency) The estimator θ achieves theCramer-Rao bound if and only if
exp−1θ θ−b(θ) =
(I− 1
3‖b‖2K(b)− 1
3Rm(C)+∇b)gradθ `.
(58)If θ is unbiased, then it achieves the Cramer-Rao bound ifand only if
exp−1θ θ =
(I− 1
3Rm(C))gradθ `. (59)
Thus the concept of estimator efficiency [25], [57], [75]depends upon the choice of affine connection, or, equivalently,the choice of geodesics onM , as evidenced by the appearanceof the∇ operator and curvature terms in Eq. (58).
Corollary 4 The variance of the estimate of thei-th coordi-nate θi is given by thei-th diagonal element of the matrixMbG−1MT
b (plus the first order term in Eq. (44) for largererrors). If θ is unbiased, then the variance of the estimate ofthe i-th coordinate is given by thei-th diagonal element of theinverse of the Fisher information matrixG−1 (plus the firstorder term in Eq. (44) for larger errors).
Many applications require bounds not on some underlyingparameter space, but on a mappingφ(θ) of that space toanother manifold. The following theorem provides the gen-eralization of the classical result. The notationφ∗ = ∂φ/∂θfrom footnote 2 is used to designate the push-forward of atangent vector (e.g., the Jacobian matrix ofφ in Rn).
Theorem 3 (Differentiable mappings) Let f , `, θ ∈ M ,and g be as in Theorem 2, and letφ : M → P be adifferentiable mapping fromM to thep-dimensional manifoldP . Given arbitrary bases(∂/∂θ1), (∂/∂θ2), . . . , (∂/∂θn),and (∂/∂φ1), (∂/∂φ2), . . . , (∂/∂φp) of the tangent spacesTθM andTφP , respectively (or, equivalently, arbitrary coor-dinates), then for any unbiased estimatorθ and its mappingφ = φ(θ),
E[(exp−1
φ φ)(exp−1φ φ)T
]≥ φ∗G−1
θ φT∗ , (60)
(Gθ)ij = g(∂/∂θi, ∂/∂θj) is the Fisher information matrix,and the push-forwardφ∗ = ∂φ/∂θ is the p-by-n Jacobianmatrix with respect to these basis vectors.
Eq. (60) in Theorem 3 may be equated with the change-of-variables formula of Eq. (11) (after taking a matrix inverse)only whenφ is one-to-one and onto. In general, neither theinverse functionθ(φ) nor its Jacobian∂θ/∂φ exist.
III. SAMPLE COVARIANCE MATRIX ESTIMATION
In this section the well-known problem of covariance matrixestimation is considered, utilizing insights from the previoussection. The intrinsic geometry of the set of covariance matri-ces is used to determine the bias and efficiency of the samplecovariance matrix (SCM).

SMITH: COVARIANCE, SUBSPACE, INTRINSIC CRAMER-RAO BOUNDS 11
Let Z = (n1,n2, . . . ,nK) be ann-by-K matrix whosecolumns are independent and identically distributed (iid) zero-mean complex Gaussian random vectors with covariance ma-trix R ∈ Pn
∼= Gl(n,C)/U(n) (also see Diaconis [18,p. 110, Chaps. 6D, 6E]; the technical details of this identi-fication in the Hermitian case involve the third isomorphismtheorem for the normal subgroup of matrices of the formejϕI).The pdf of Z is f(Z|R) =
((πn detR)−1e− tr RR−1)K
,whereR = K−1ZZH is the SCM. The log-likelihood of thisfunction is (ignoring constants)
`(Z|R) = −K(tr RR−1 + log detR). (61)
We wish to compute the Cramer-Rao bounds on the covari-ance matrixR and examine in which sense the SCMR(the maximum likelihood estimate) achieves these bounds.By Theorem 1, we may extract the second-order terms of`(Z|R + D) in D to compute the FIM. These terms followimmediately from the Taylor series
tr(R + D)−1A = trR−1A− trDR−1AR−1
+ tr(DR−1)2AR−1 + · · · , (62)
log det(R + D) = log detR + trDR−1
− 12 tr(DR−1)2 + · · · , (63)
whereA and D are arbitrary Hermitian matrices. It followsthat the FIM forR is given by
gcov(D,D) = −E [∇2`] = K tr(DR−1)2, (64)
that is, the Fisher information metric for Gaussian covariancematrix estimation is simply the natural Riemannian metricon Pn given in Eq. (4) (scaled byK, i.e., gcov = K·gR);this also corresponds to the natural metric on the symmetriccone Gl(n,C)/U(n) [24]. Given the central limit theoremand the invariance of this metric, this result is not too surpris-ing.
A. Natural Covariance Metric CRB
The formula for distances using the natural metric onPn
of Eq. (4) is given by the2-norm of the vector of logarithmsof the generalized eigenvalues between two positive-definitematrices, i.e.,
dcov(R1,R2) =(∑
k
(log λk)2)1/2
, (65)
where λk are the generalized eigenvalues of the pen-cil R1 − λR2 or, equivalently, R2 − λR1. If multi-plied by 10/ log 10, this distance between two covariancematrices is measured in decibels, i.e.,dcov(R1,R2) =(∑
k(10· log10 λk)2)1/2
(dB); using Matlab notation, it isexpressed asnorm(10*log10(eig(R1,R2))) . This dis-tance corresponds to the formula for the Fisher informationmetric for the multivariate normal distribution [54], [61]. ThemanifoldPn with its natural invariant metric isnot flat simplybecause, inter alia, it is not a vector space, its Riemannianmetric is not constant, its geodesics are not straight lines[Eq. (67)], and its Christoffel symbols are nonzero [Eq. (66)].
GeodesicsR(t) = expR(tD) on the covariance matricesPn
corresponding to its natural metric of Eq. (4) satisfy thegeodesic equationR + Γcov(R, R) = 0, where the Christoffelsymbols are given by the quadratic form
Γcov(A,B) = −12(AR−1B + BR−1A
)(66)
(see footnote 6). A geodesic emanating fromR in the directionD ∈ TRPn has the form
expR(tD) = R12 exp(tR− 1
2 DR− 12 )R
12 , (67)
whereR12 is the unique positive-definite symmetric (Hermi-
tian) square root ofR and “exp” without a subscript denotesthe matrix exponentialeAt = I + At+ (t2/2)A2 + · · · . Thisis equivalent to the representationR(t) = R
12 etD0R
12 , where
D0 is a tangent vector atI [trD20 = 1 for unit vectors]
corresponding toD [tr(DR−1)2 = 1 for unit vectors] bythe coloring transformation
D = R12 D0R
12 . (68)
The appearance of the matrix exponential in Eq. (67), and inEq. (120) of Section IV-C for subspace geodesics, explains the“exp” notation for geodesics described in footnote 6 [see alsoEq. (69)]. From the expression for geodesics in Eq. (67), theinverse exponential map is
exp−1R R = R
12 (log R− 1
2 RR− 12 )R
12 (69)
(unique matrix square root and logarithm of positive-definiteHermitian matrices). Because Cramer-Rao analysis providestight estimation bounds at high SNRs, the explicit use ofthese geodesic formulas is not typically required; however,the metric of Eq. (65) corresponding to this formula is usefulto measure distances between covariance matrices.
In the simple case of covariance matrices, the FIM and itsinverse may be expressed in closed form. To compute CRBsfor covariance matrices, the followingn2 orthonormal basisvectors for the tangent space ofPn (Hermitian matrices inthis section) atI are necessary:
D0ii = an n-by-n symmetric matrix whose
i-th diagonal element is unity, zeroselsewhere,
(70)
D0ij = an n-by-n symmetric matrix whose
ij-th andji-th elements are both
2−12 , zeros elsewhere (i < j);
(71)
Dh0ij = an n-by-n Hermitian matrix whose
ij-th element is2−12√−1, andji-th
element is−2−12√−1, zeros
elsewhere (i < j).
(72)
There aren real parameters along the diagonal ofR plus2· 12n(n − 1) real parameters in the off-diagonals, for a totalof n2 parameters. For example, the2-by-2 Hermitian matrix(
ac−jd
c+jdb
)is decomposed using four orthonormal basis
vectors as(a
c−jdc+jd
b
)= a
(10
00
)+ b(
00
01
)+ 2
12 c( 0
2−12
2−12
0
)+ 2
12 d( 0
−j2−12
j2−12
0
)(73)

12 TO APPEAR IN IEEE TRANS. SIGNAL PROCESSING
and is therefore represented by the real4-vector(a, b, 2
12 c, 2
12 d). To obtain an orthonormal basis for the
tangent space ofPn at R, color the basis vectors by pre- andpost-multiplying byR
12 as in Eq. (68), i.e.,
Dhij = R
12 Dh0
ij R12 , (74)
where the superscript ‘h’ denotes a flag for using either theHermitian basis vectorsDh0
ij or the symmetric basis vectors
D0ij ; for notational convenience,Dh0
iidef= D0
ii is implied.With respect to this basis, Eq. (64) yields metric coefficients
(Gcov)hij;h′i′j′ = gcov(Dh
ij ,Dh′i′j′
)= Kδhh′δii′δjj′
(75)(Kronecker delta), that is,Gcov = KIn2 .
A closed-form inversion formula for the covariance FIM iseasily obtained via Eq. (48) in footnote 8. The fact that theHermitian matrices are self-dual is used, i.e., ifU is a linearmapping from the Hermitian matrices toR, thenU may alsobe represented as a Hermitian matrix itself via the definition
U(X) def= trUX (76)
for all Hermitian matricesX. The inverse of the Fisherinformation metric (see footnote 8) is defined by the equation
g−1cov(U,U) = gcov(D,D) (77)
for all D, where D and U are related by the equationgcov(D,X) = U(X) = trUX for all X. Clearly, fromEq. (64)
U = KR−1DR−1, (78)
D = K−1RUR. (79)
Applying Eqs. (77) and (79) to Eq. (64) yields the formula
g−1cov(U,U) = K−1 trRURU. (80)
To compute the coefficients of the inverse FIM with respectto the basis vectors of Eq. (74), the dual basis vectors
Dh∗ij = R− 1
2 Dh0ij R− 1
2 (81)
are used; note thatDh∗ij
(Dh′
i′j′
)= trDh∗
ij Dh′i′j′ =
δhh′δii′δjj′ .We now have sufficient machinery to prove the following
theorem.
Theorem 4 The Cramer-Rao bound on the natural distance[Eq. (65)] betweenR and any unbiased covariance matrixestimatorR of R is
εcov ≥n
K1/2(Hermitian case), (82)
εcov ≥(n(n+ 1)
)1/2
K1/2(real symmetric case), (83)
where εcov = E [d2cov(R,R)]1/2 is the root-mean-square
error, and the Riemannian curvature termRm(C) has beenneglected. To convert this distance to decibels, multiplyεcovby 10/ log 10.
Proof: The square error of the covariance measured using thenatural distance of Eq. (65) is
ε2cov =∑
i
(Dii)2 + 2∑i<j
((Dij)2 + (Dij
h )2), (84)
where each of theDii are the coefficients of the basis vectorsDii in Eq. (74) and2
12Dij
h (i < j) are the coefficients of the
orthonormal basis vectorsDhij in the vector decomposition
D =∑
i
DiiDii +∑i<j
212 (DijDij +Dij
h Dhij). (85)
Eq. (84) follows from the consequence of Eqs. (65) and (67):the natural distance between covariance matrices alonggeodesics is given by
dcov
(R(t),R
)= |t|
(tr(DR−1)2
)1/2, (86)
which is simply the Frobenius norm of the whitened matrixtR− 1
2 DR− 12 (see also footnote 6). Therefore, the CRB of the
natural distance is given by
ε2cov ≥ trG−1cov, (87)
whereGcov is computed with respect to the coefficientsDii
and212Dij
h. Either by Eq. (75),G−1cov = K−1In2 , or by Eqs.
(80) and (81),
(G−1cov)
hij;hij = g−1cov
(Dh∗
ij ,Dh∗ij
)= K−1 tr
(Dh0
ij
)2 = K−1 (88)
for i ≤ j, which establishes the theorem. The real symmetriccase follows becauseG−1
cov = 2·K−1I 12 n(n+1) [n real param-
eters along the diagonal ofR plus 12n(n− 1) real parameters
in the off-diagonals; the additional factor of2 comes from thereal Gaussian pdf of Eq. (110)].
B. Flat Covariance Metric CRB
The flat metric on the space covariance matrices expressedusing the Frobenius norm is oftentimes encountered:
d covflat
(R1,R2) =(tr(R1 −R2)2
)1/2 = ‖R1 −R2‖F . (89)
Theorem 5 The Cramer-Rao bound on the flat distance[Eq. (89)] between any unbiased covariance matrix estimatorR and R is
ε covflat
≥
(∑i(R
ii)2 + 2∑
i<j RiiRjj
K
)1/2
(90)
(Hermitian case), whereε covflat
= E [d2covflat
(R,R)]1/2 is the root-
mean-square error (flat distance) andRij denotes theij-th el-ement ofR. In the real symmetric case, the scale factor in thenumerator of Eq. (90) is2
(∑i≤j(R
ij)2 +∑
i<j RiiRjj
). The
flat and natural Cramer-Rao bounds of Theorem 4 coincidewhenR = I.
Proof: The proof recapitulates that of Theorem 4. For theflat metric of Eq. (89), bounds are required on the individualcoefficients of the covariance matrix itself, i.e.,Rii for the

SMITH: COVARIANCE, SUBSPACE, INTRINSIC CRAMER-RAO BOUNDS 13
diagonals ofR and 212Rij
h for the real and imaginary off-diagonals. Using these parameters,
ε2covflat
=∑
i
(Rii)2 + 2∑i<j
((Rij)2 + (Rij
h )2), (91)
where the covarianceR is decomposed as the linear sum
R =∑
i
RiiD0ii +
∑i<j
212 (RijD0
ij +Rijh Dh0
ij ). (92)
With respect to the orthonormal basis vectorsD0ii andDh0
ij
of Eqs. (70)–(72), the coefficients of the inverse FIMG−1covflat
are(G−1
covflat
)hij;h′i′j′ = g−1cov
(Dh0
ij ,Dh′0i′j′
)= K−1 trRDh0
ij RDh′0i′j′ . (93)
The CRB on the flat distance is
ε2covflat
≥ trG−1covflat. (94)
A straightforward computation shows that(G−1
covflat
)ii;ii = (Rii)2 (i = 1, . . . , n),
(95)(G−1
covflat
)ij;ij = RiiRjj + (Rij)2 − (Rijh )2 (i < j),
(96)(G−1
covflat
)h,ij;h,ij = RiiRjj − (Rij)2 + (Rijh )2 (i < j),
(97)
establishing the theorem upon summing overi ≤ j.
C. Efficiency and Bias of the Sample Covariance Matrix
We now have established the tools with which to examinethe intrinsic bias and efficiency of the sample covariancematrix R = K−1ZZH in the sense of Eq. (23) and Corol-lary 3. Obviously E [R] = R, but this linear expectationoperation means the integral
∫Rf(Z|R) dZ, which treats
the covariance matrices as a convex cone [24] included inthe vector spaceRn2
(R 12 n(n+1) for the real, symmetric
case; a convex cone is a subset of a vector space that isclosed under addition and multiplication by positive real num-bers). Instead of standard linear expectation valid for vectorspaces, the expectation ofR is interpreted intrinsically asER[R] = expR
∫(exp−1
R R)f(Z|R) dZ for various choicesof geodesics onPn as in Eq. (22).
First, observe from the first-order terms of Eqs. (62) and(63) that
d`(D) = K(trDR−1RR−1 − trDR−1), (98)
establishing thatR maximizes the likelihood. Because theSCM R is the maximum likelihood estimate, it is asymptoti-cally efficient [17], [75], independent of the geodesics chosenfor Pn. From the definition of the gradient (see footnote 8),d`(D) = gcov(gradR `,D) for all D ∈ TRPn; therefore, withrespect to the FIMgcov,
gradR ` = R−R. (99)
The well-known case of the flat metric/connection onPn isexamined first. Flat distances betweenR andR are given bythe Frobenius norm‖R−R‖F as in Eq. (89), and the geodesicbetween these covariance matrices isR(t) = R + t(R−R),0 ≤ t ≤ 1. Obviously for the flat connection,exp−1
R R =R−R.
Theorem 6 The sample covariance matrixR is an unbiasedand efficient estimator of the covarianceR with respect to theflat metric on the space of covariance matricesPn.
Proof: Trivially, ER[R] = R + E [R − R] = R for theflat metric, soR is unbiased with respect to this metric. ByCorollary 3, an unbiased estimatorR is efficient if exp−1
R R =gradR `, which by Eq. (99) is true for the flat metric.
The flat metric onPn has several undesirable practicalproperties. It is well known that the SCM is not a very goodestimate ofR for small sample sizesK (which leads to ad hoctechniques such as diagonal loading [64] and reference priormethods [78]), but this dependence of estimation quality onsample support is not fully revealed in Theorem 6, whichensures that the SCM always achieves the best accuracypossible. Also, in many applications, treating the space ofcovariance matrices as a vector space may lead to degradedalgorithm performance, especially when a projection onto sub-manifolds ofPn (structured covariance matrices) is desired [8].The flat metric has undesirable geometric properties as well.Because the positive-definite Hermitian matrices are convex,every point on straight-line geodesics is also a positive-definite Hermitian matrix. Nevertheless, these paths may notbe extended indefinitely to allt ∈ R. Therefore, the spacePn endowed with the flat metric is not geodesically complete,i.e., it is not a complete metric space. Furthermore, and muchmore significantly for applications, the flat connection is notinvariant to the group actionR 7→ ARAH of Gl(n,C) onthe positive-definite Hermitian matrices, i.e.,d cov
flat(R1,R2) 6=
d covflat
(AR1AH,AR2AH). Therefore, the CRB depends uponthe underlying covariance matrixR as seen in Theorem 5.
In contrast, the natural metric onPn in Eq. (65) has noneof these defects and reveals some remarkable properties aboutthe SCM, as well as yielding root-mean-square errors that areconsistent with the dependence on sample size observed intheory and practice (Figure 3). The natural distance RMSEvaries with the sample size relative to the Cramer-Rao bound,unlike the flat distance RMSE, whose corresponding estimatoris efficient and therefore equals its Cramer-Rao lower bound atall sample sizes. Furthermore, the natural metric is invariantto the group action ofGl(n,C); therefore, it yields boundsthat are independent of the underlying covariance matrixR.Also, Pn endowed with this metric is a geodesically completespace. Because the natural Riemannian metric onPn [Eq. (65)]has the properties of accounting for the change in estimationquality of the SCM as the sample size varies, being invariantto the group action ofGl(n,C) and therefore independentof R, and yielding a complete metric space forPn, it isrecommended for the analysis of covariance matrix estimationproblems.

14 TO APPEAR IN IEEE TRANS. SIGNAL PROCESSING
Theorem 7 The sample covariance matrix estimatorR withrespect to the natural metric onPn is biased and not efficient.The bias vector field and expectation ofR with respect toRare
B(R) = E [exp−1R R] = −β(n,K)R, (100)
ER[R] = expR B(R) = e−β(n,K)R, (101)
where
β(n,K) =1n
(n logK + n− ψ(K − n+ 1)
+ (K − n+ 1)ψ(K − n+ 2)
+ ψ(K + 1)− (K + 1)ψ(K + 2))
(102)
(Hermitian case) andψ(z) = Γ′(z)/Γ(z) is the digammafunction. In the real symmetric case,β(n,K) = logK −log 2−n−1
∑ni=1 ψ
(12 (K − i+ 1)
). Furthermore, this bias is
parallel and the matrix of sectional curvature terms vanishes,i.e.,
∇B ≡ 0 and K(B) ≡ 0. (103)
Proof: From the definition of the bias vector in Eq. (23)and the inverse exponential in Eq. (69),B(R) =R
12 E [log R− 1
2 RR− 12 ]R
12 = R
12 E [log R0]R
12 , where
R0 = R− 12 RR− 1
2 is the whitened SCM. Therefore,the bias of the SCM is given by the colored expecta-tion of log R0. The whitened SCMR0 has the com-plex Wishart distributionCWK(n,K−1I). Using the eigen-value decomposition ofR0 = QΛQH, E [log R0] =E [Q(log Λ)QH] = E [qqH]E [tr log Λ], where q is an ar-bitrary column of Q, the last equality following from theindependence of eigenvalues and eigenvectors [45]. For theeigenvector part,E [qqH] = n−1I becauseq = n/‖n‖2for a complex normal vectorn (zero mean, unit variance).For the eigenvalue part,E [tr log Λ] = E [log detΛ] =E [log det R0], and the distribution ofdet R0 is the sameasK−n
∏ni=1 χ
2K−i+1, the product of independent complex
chi-squared random variables [fχ2ν(z) = Γ(ν)−1zν−1e−z;
Muirhead’s Theorem 3.2.15 [45] contains the real case]. There-fore, E [log det R0] = E
[−n logK +
∑ni=1 logχ2
K−i+1
]=
−n logK +∑n
i=1 ψ(K − i+ 1), whereψ(z) is the digammafunction. Applying standard identities forψ(z) evaluated atthe integers yieldsE [log det R0] = −n·β(n,K) of Eq. (102).Therefore, E [log R0] = −β(n,K)I and thus B(R) =−β(n,K)R, establishing the first part of the theorem. Theproof of the real case is left as an exercise.
To prove that the SCM is not efficient,∇B must becomputed. Using the description of the covariant deriva-tive in footnote 5, (∇B)(D) = ∇DB = B(0) +Γcov
(B(0),D
)for any vector fieldB(t) = B(expR tD)
along the geodesicR(t) = expR(tD). For the bias vectorfield, B(t) = −β(n,K)R(t) = −β(n,K) expR(tD) andB(0) = −β(n,K)D. Applying the Christoffel symbols ofEq. (66),∇DB = B(0)− 1
2
(B(0)R−1D + DR−1B(0)
)=
−β(n,K)D + 12β(n,K)(D + D) = 0. This is true for arbi-
trary D; therefore,∇B ≡ 0 and the bias of the SCM is
parallel. This fact can also be shown using the explicit formulafor parallel translation onPn and Eq. (15):
τtB0 = R12 e
12 tR− 1
2 DR− 12 R− 1
2 B0R− 12 e
12 tR− 1
2 DR− 12 R
12 .
(104)The proof that the SCM is not efficient is completed by observ-ing that Eq. (58) in Corollary 3 does not hold forexp−1
R R ofEq. (69),B(R) of Eq. (100), andgradR ` of Eq. (99). Finally,computing the matrixK(B) defined in Eq. (33) atR = IgivesK(B) = K
(−β(n,K)I
)= 0, because the formula for
the sectional curvature ofPn, KPn(X ∧Y ) = − 14‖[X,Y ]‖2
[Eq. (28) of footnote 7] vanishes trivially forX = −β(n,K)I.By invariance,K(B) ≡ 0 for all R.
It is interesting to note that both∇B and K(B) vanish(conveniently) because the SCM’s bias vector is tangent tothe 1-dimensional Euclidean part of the symmetric spacedecomposition [30, chap. 5, sec. 4]Pn
∼= Gl(n)/SO(n) ∼=R×Sl(n)/SO(n), where theR-part represents the determi-nant of the covariance matrix. That is, the SCM’s determinantis biased, but it is otherwise unbiased.
Theorem 7 is of central importance because it quantifies theestimation quality of the sample covariance matrix, especiallyat low sample support.
Corollary 5 The Cramer-Rao bound of the natural distanceof the SCM estimateR from R is
ε2cov ≥n2
K+ nβ(n,K)2 (105)
(Hermitian case), whereε2cov = E [d2cov(R,R)] is the mean-
square error,β(n,K) is defined in Eq. (102), and the Rie-mannian curvature termRm(C) has been neglected.
Proof: The proof is an application of Eq. (54) of Corollary 1.BecauseB(R) is parallel, the bound onE [d2
cov(R,R)] isgiven bytrG−1
cov +trB(R)⊗B(R), where the tensor productis interpreted to be the outer product over then2-dimensionalvector spaceTRPn, not the Kronecker product of matrices.The first part of this sum is established in Eq. (82) ofTheorem 4, and the second part by the fact that the traceof the outer product of two vectors equals their inner product:trB(R) ⊗ B(R) = gR
(B(R),B(R)
)= tr
(β(n,K)2In
)=
nβ(n,K)2.
An expression for the Riemannian curvature termRm(C)for the SCM, which becomes significant for errors of or-der (10/ log 10)(max |KPn
|)−1/2 = (10/ log 10)2 ≈ 8.7 dB,is possible using Eq. (28) of footnote 7. AtR = I, letX = exp−1
I R0 = log R0 ≈ R0 − I and let D ∈ TIPn
be a Hermitian matrix. Then
〈Rm(C) ·D,D〉 = E[〈R(X,D) ·D,X〉
],
= E[‖X ∧D‖2KPn
(X ∧D)],
= E[− 1
4‖[X,D]‖2],
= 14 E[tr([R0,D])2
], (106)
where [X,Y ] = XY − YX is the Lie bracket. It can beshown that〈Rm(C)·Dh0
ij ,Dh0ij 〉 = − 1
2 (n−1)/K if i = j,and− 1
2n/K if i 6= j.

SMITH: COVARIANCE, SUBSPACE, INTRINSIC CRAMER-RAO BOUNDS 15
100
101
102
Sample support / n
100
101
102
Co
vari
ance
RM
SE
(d
B)
Natural metricBiased natural CRBUnbiased natural CRBFlat metricFlat unbiased CRB
Fig. 3. CRB and RMSE of the distance onP6 (in decibels, Hermitian case) ofthe SCMR from R versus sample support. A Monte Carlo simulation is usedwith 1000 trials and Wishart distributed SCMs.R itself is chosen randomlyfrom a Wishart distribution. The unbiased natural CRB [Eq. (82), dottedcyan]is shown below the biased natural CRB [Eq. (105), solidred], which is itselfbelow the unbiased flat CRB [Eq. (90), solidmagenta]. The RMSEs of thenatural and flat (Frobenius) distances of Eqs. (65) and (89) are the dashed (bluebelow green) curves (respectively). Because the SCM w.r.t. the flat metric isan efficient estimator, the RMSE lies on top of its CRB; however, unlike the(inefficient) natural distance, the (efficient) flat distance does not accuratelyreflect the varying quality of the covariance matrix estimates as the samplesize varies, as does the natural distance [Theorem 7 and Corollary 5]. TheSCM w.r.t. the natural metric is biased and inefficient, and therefore does notachieve the biased natural CRB. Nevertheless, the maximum likelihood SCMis always asymptotically efficient. The SCM’s Riemannian curvature terms,which become significant for covariance errors on the order of8.7 dB, havebeen neglected.
A connection can also be made with asymptotic results forthe eigenvalue spectrum of the SCM. The largest and smallesteigenvaluesλmax and λmin of the whitened SCMR0 areapproximated by
λmin, max ≈(1±
√n/K
)2
(107)
(n large,K ≥ n) [35], [59]. ForK ≈ n, the extreme spectralvalues of R0 differ considerably from unity, even thoughE [R0] = I for all K, and this estimator is efficient withrespect to the flat connection. Indeed, by the deformed quarter-circle law [35], [40], [60] for the asymptotic distribution ofthe spectrum ofR0 (largen), the mean square of the naturaldistance ofR0 from I is
E [n−1d2cov(R0, I)] ∼
12πy
∫ (1+√
y)2
(1−√y)2(log λ)2
×((1 +
√y)2 − λ
) 12(λ− (1−√y)2
) 12
λdλ
= y +56y2 +O(y3) (108)
(n→∞), wherey = n/K ≤ 1. For largen and large samplesupport (i.e., smally), the SCM’s (biased) CRB in Eq. (105)has the asymptotic expansion
n−1ε2cov ∼ y +14y2 +O(y3) (n→∞), (109)
whose linear term iny coincides exactly with that of Eq. (108)because the SCM is asymptotically efficient. The SCM is notefficient for y > 0 (finite sample support), and the quadraticterms of Eqs. (108) and (109) differ, with the CRB’s quadraticterm (14y
2) being strictly less than the mean-square error’squadratic term (56y
2; adding the SCM’s Riemannian curvatureterms from Eq. (106) adds a term of1
3 (n2 − 1)/K2 ∼ 13y
2,resulting in 7
12y2 < 5
6y2). We note in passing the similarity
between the first-order term iny = n/K of this Cramer-Raobound and the well-known Reed-Mallett-Brennan estimationloss for adaptive detectors [55], [64].
IV. SUBSPACE ANDCOVARIANCE ESTIMATION ACCURACY
We now return to the analysis of estimating an unknownsubspace with an underlying unknown covariance matrix givenin Eq. (1). The parameter space is the product manifoldM = Pp×Gn,p, with the covariance matrix being an unknownnuisance parameter. The dimension of this product manifoldis the sum of the dimensions ofPp andGn,p, which equals12p(p+ 1) + p(n− p) in the real case andp2 + 2p(n− p) inthe proper complex case. We will focus on the real case inthis section; the proper complex case is a trivial extension.
A. The Subspace and Covariance Probability Model
Let Z = (z1, z2, . . . , zK) be a realn-by-K matrix whosecolumns are iid random vectors defined by Eq. (1). The jointpdf of this data matrix is
f(Z|R1,Y) =
(e−
12 trR−1
2 R((2π)n detR2
)1/2
)K
(110)
R2 = YR1YT + R0, (111)
whereR = K−1ZZT is the sample covariance matrix and then-by-p andp-by-p matricesY andR1 represent the unknownsubspace and covariance, respectively. The log-likelihood ofthis function is (ignoring constants)
`(Z|R1,Y) = − 12K(trR−1
2 R + log detR2). (112)
The maximum likelihood estimate of the subspace is simplythep-dimensional principal invariant subspace of the whitenedSCM R0 = R− 1
20 RR− 1
20 . Indeed, a straightforward compu-
tation involving the first-order terms of Eqs. (62) and (63)establishes that solving the equation∂`/∂Y = 0 results inthe invariant subspace equation [22]
R0Y − Y(YTR0Y) = 0
for Y, such thatYTY = I. ChoosingY to be the invariantsubspace corresponding to the largest eigenvalues ofR0
maximizes the log-likelihood.
B. The Natural Geometry of Subspaces
Closed-form expressions for Cramer-Rao bounds on theparametersR1 andY are obtained if points on the Grassmannmanifold are represented byn-by-p matricesY such that
YTR−10 Y = I, (113)

16 TO APPEAR IN IEEE TRANS. SIGNAL PROCESSING
and post-multiplication of any such matrix by an orthogonalp-by-p matrix represents the same point in the equivalenceclass. This constraint is a colored version of the convenientrepresentation of points onGn,p by matrices with orthonor-mal columns [1], [22] and simply amounts to the whiteningtransformation
Y = R− 12
0 Y (114)
where YTY = I. Given such a matrixY with orthonormalcolumns, or, equivalently,Y = R
120 Y satisfying Eq. (113),
tangent vectors to the Grassmann manifold are represented byn-by-p matrices∆ ∈ TYGn,p or ∆ = R
120 ∆ (colored case)
of the form
∆ = Y⊥B (whitened case), (115)
∆ = Y⊥B = R120 Y⊥B (colored case), (116)
such thatYT∆ = 0 andYTR−10 ∆ = 0, or, equivalently,Y⊥
is an arbitraryn-by-(n− p) matrix with orthonormal columns
such thatYTY⊥ = 0 and YT⊥Y⊥ = I, Y⊥ = R
120 Y⊥, andB
is an arbitrary(n− p)-by-p matrix [22]. Cotangent vectorsin T ∗
YGn,p (whitened case) are also represented byn-by-p
matricesΥ = Y⊥B with the identification
Υ(∆) def= tr ΥT∆ (117)
for all ∆ such that YT∆ = 0. In the colored case,Υ(∆) = Υ(∆) = trΥT∆ = tr ΥT∆; therefore,Υ =R− 1
20 Υ = R− 1
20 Y⊥B, andYTΥ = 0. As usual, dual vectors
are whitened contravariantly.The CRB for the unknown subspace will be computed using
the natural metric onGn,p given by [22]
gss(∆, ∆) = tr ∆T(I− YYT)∆ = tr∆TR−10 ∆. (118)
Distances corresponding to this metric are give by the2-normof the vector of principal angles between two subspaces, i.e.,
dss(Y1, Y2) =(∑
k
θ2k
)1/2
, (119)
0 ≤ θk ≤ π2 , where cos θk are the singular values of the
matrix YT1 Y2. This distance between two subspaces is
measured in radians; in Matlab notation it is expressed asnorm(acos(svd(orth(Y1)’*orth(Y2)))) . Thereare several other subspace distances that are definedby embeddings of the Grassmann manifold in higherdimensional manifolds [22, p. 337]. Both the arccosineimplicit in Eq. (119) and the logarithm for the natural metriconPp in Eq. (65) correspond to the inverse of the exponentialmap “exp−1” discussed in Section II-B.
Applying Eq. (115) to Eq. (118) shows that the naturaldistance between two nearby subspaces is given by the Frobe-nius norm of the matrixB (‖B‖2F = trBTB). Therefore, theCRB of the natural subspace distance is given by the FIMwith respect to the elements ofB. This fact is made rigorousby the following observations. Geodesics on the Grassmannmanifold Gn,p corresponding to its natural metric are givenby the formula [22]
Y(t) = YV cos(Σt)VT + U sin(Σt)VT, (120)
whereUΣVT := ∆ is the compact singular value decompo-sition of the tangent vector∆ at Y (YTY = I, YT∆ = 0).For the proper complex case, the transpositions in Eq. (120)may be replaced with conjugate transpositions. Furthermore,it may be verified that for the case of geodesics provided inEq. (120)
dss
(Y(t), Y
)= |t|(tr ∆T∆)1/2 (121)
(see also Eq. (86) for covariance matrices and footnote 6 forthe general case). Geodesics for subspaces satisfy the dif-ferential equationY + Γss(Y, Y) = 0, where the Christoffelsymbols for the Grassmann manifoldGn,p are given by thequadratic form [22]
Γss(∆, ∆) = Y∆T∆. (122)
The inverse exponential map is given byexp−1
YY = UΣVT,
where these matrices are computed with the compact SVDsU1C1VT
1 := YTY (singular values in ascending order)andU2S2VT
2 := YU1VT1 − YV1C1VT
1 (singular values indescending order), and the formulasU = U2VT
2V1, Σ =arccosC1 (principal values), andV = V1. ThenYU1VT =YV(cosΣ)VT + U(sinΣ)VT; note that S2 = sinΣ andVT
2V1 = diag(±1, . . . ,±1).
C. Subspace and Covariance FIM and CRB
Theorem 1 ensures that we may extract the second-orderterms of (Z|R1+D,Y+∆) in D and∆ to compute the FIM.The Fisher information metric for the subspace plus covarianceestimation problem of Eq. (1) is obtained by using the second-order terms of the Taylor series given in Eqs. (62) and (63)along with Eq. (16) and the perturbation
(Y+∆)(R1+D)(Y+∆)T+R0 = R2+R(1)2 +R(2)
2 , (123)
where the first- and second-order terms are
R(1)2 = ∆R1YT + YR1∆T + YDYT, (124)
R(2)2 = ∆R1∆T + ∆DYT + YD∆T. (125)
The resulting FIM is given by the quadratic form
gcov,ss
((D,∆), (D,∆)
)= 1
2K tr((∆R1YT + YR1∆T + YDYT)R−1
2
)2. (126)
Only the 1st-order terms of Eq. (123) appear, and Eq. (126) isconsistent with the well-known case of stochastic CRBs [57]:(G)ij = tr
(R−1
2 (∂R2/∂θi)R−1
2 (∂R2/∂θj))
for the parame-tersθ1, θ2, . . . , θn. Applying the Woodbury formula
R−12 = R−1
0 −R−10 Y(R−1
1 + YTR−10 Y)−1YTR−1
0 (127)
to Eq. (126) and the constraint of Eq. (113) yields thesimplified FIM for the covariance and subspace estimationproblem:
gcov,ss
((D1,∆1), (D2,∆2)
)= 1
2K tr(I + R1)−1D1(I + R1)−1D2
+K trR21(I + R1)−1∆T
1R−10 ∆2. (128)

SMITH: COVARIANCE, SUBSPACE, INTRINSIC CRAMER-RAO BOUNDS 17
In the proper complex case, Eq. (128) may be modifiedby removing the factor of12 that appears in the front andreplacing the transpose operator with the Hermitian (conju-gate transpose) operator. There are no cross terms betweenthe covariance and subspace components of the joint FIM;therefore, there is no estimation loss on the subspace in thisexample.
Cramer-Rao bounds on the covariance and subspace param-eters are obtained by computing the inverse metricg−1
cov,ss (asdescribed in footnote 8). This inverse is given by the equation
g−1cov,ss
((U,Υ), (U,Υ)
)= gcov,ss
((D,∆), (D,∆)
), (129)
where the cotangent vectorsU ∈ T ∗R1Pp and Υ ∈ T ∗YGn,p
(colored) are defined by the equationU(D′) + Υ(∆′) =gcov,ss
((D,∆), (D′,∆′)
)for all tangent vectorsD′ ∈ TR1Pp
and∆′ ∈ TYGn,p (colored). Using Eqs. (76), (117), and (128)to solve forD and∆ as functions ofU andΥ yields
D =2K
(I + R1)U(I + R1), (130)
∆ =1K
R0ΥR−21 (I + R1). (131)
Finally, these expressions forD and∆ may be inserted intoEq. (129) to obtain the inverse Fisher information metric
g−1cov,ss
((U1,Υ1), (U2,Υ2)
)=
2K
tr(I + R1)U1(I + R1)U2
+1K
trR−21 (I + R1)ΥT
1R0Υ2. (132)
D. Computation of the Subspace CRB
The inverse Fisher information metric of Eq. (132) pro-vides the Cramer-Rao bound on the natural subspace distancebetween the true subspace and any unbiased estimate of it.Because this distance corresponds to the Frobenius norm ofthe elements of the matrixB in Eq. (115), the FIM and inverseFIM will be computed with respect to the basis of the tangentspace ofGn,p using these elements and the correspondingdual basis of the cotangent space. Using classical Cramer-Raoterminology, we will compute a lower bound on the root-mean-square subspace error
εss = E [d2ss(Y,Y)]1/2 = E
[∑i,j
(Bij)2]1/2
(133)
between an estimateY of Y, whereBij are the elements ofB.The orthonormal basis vectors (whitened case) ofTYGn,p are
∆ij = Y⊥Bij : 1 ≤ i ≤ n− p, 1 ≤ j ≤ p (134)
Y⊥ = an arbitraryn-by-(n− p) matrix
such thatYTY⊥ = 0, YT⊥Y⊥ = I,
(135)
Bij = an (n− p)-by-p matrix whoseij-thelement is unity, zeros elsewhere.
(136)
For convenience, we will also use the orthonormal basisvectorsDij for the tangent space ofPp defined in Eq. (74),
though the invariance of the subspace accuracy to this choiceof basis ensures that this choice is arbitrary.
The full FIM for the subspace and nuisance covarianceparameters is written conveniently in block form as
G =(
C XXT S
), (137)
whereC is a square matrix of orderdimPp representing thecovariance block,S is a square matrix of orderdimGn,p rep-resenting the subspace block, andX is adimPp-by-dimGn,p
matrix that represents the cross terms, which vanish inthis example. Using the Fisher information metricgcov,ss ofEq. (128), the coefficients of these blocks are
(C)ij;i′j′ = gcov,ss
((Dij ,0), (Di′j′ ,0)
), (138)
(S)ij;i′j′ = gcov,ss
((0,∆ij), (0,∆i′j′)
), (139)
(X)ij;i′j′ = gcov,ss
((Dij ,0), (0,∆i′j′)
). (140)
Note that a basis for the tangent space of the product manifoldPp × Gn,p must be used, analogous to standard Cramer-Raoanalysis with a nuisance parameter. The CRB for the subspaceaccuracy is given by the lower-right subspace block ofG−1,which is expressed using the inverse of the Schur complementof C as
ΣS = (S−XTC−1X)−1. (141)
The bound on the subspace estimation accuracy is then givenby the formula
ε2ss ≥ trΣS, (142)
whereεss is the RMSE defined in Eq. (133), and the sectionaland Riemannian curvature termsK(b) andRm(C) have beenneglected. The invariance of this result to any particular basisfor the tangent space of the covariance matrices may be seenby substitutingC 7→ ACAT and X 7→ AX into Eq. (141)for an arbitrary invertible matrixA, as in standard Cramer-Rao analysis. For problems in which the cross termsX ofEq. (137) are nonzero,ΣS in Eq. (141) quantifies the lossin measurement accuracy associated with the necessity ofestimating the nuisance parameters.
Alternatively, the formula for the inverse FIM of Eq. (132)may be used to computeΣS:
(ΣS)ij;i′j′ = g−1cov,ss
((0,∆∗
ij), (0,∆∗i′j′)
),
= K−1 trR−21 (I + R1)BT
ijBi′j′ ,(143)
where∆∗ij = R− 1
20 Y⊥Bij is the (colored) dual basis vector
of ∆ij = R120 ∆ij in Eq. (134).
In the specific caseR1 = SNR·I (but unknown), whereSNR is the signal-to-noise ratio, the blocks of the FIM inEq. (137) with respect to the basis vectors above simplify to
S =K·SNR2
1 + SNRIp(n−p),
C =K·SNR2
2(1 + SNR)2I 1
2 p(p+1),
X = 0.
(144)

18 TO APPEAR IN IEEE TRANS. SIGNAL PROCESSING
1010
–3
10–2
10–1
SNR (dB)
Su
bsp
ace
RM
SE
(ra
d)
20 30 40
Unwhitened SVDWhitened SVDSubspace CRB
Fig. 4. RMSEs of the whitened and unwhitened SVD-based subspaceestimator (Section IV-E) and the CRB of Eq. (143) versus SNR for theestimation problem of Eq. (1) onG5,2. R0 and R1 are chosen randomlyfrom a Wishart distribution, andY is chosen randomly from the uniformdistribution onGn,p [orth(randn(n,p)) in Matlab notation]. The RMSEof the unwhitened SVD estimate is the dashed (green) curve, which exceedsthe RMSE of the whitened SVD estimate (dashedblue curve) because ofthe bias induced byR0. Below these curves is the CRB in the solid (red)curve. A constant sample support of10 = 5p snapshots and 1000 MonteCarlo trials are used. The RMSEs of the SVD-based subspace estimators area small constant fraction above the Cramer-Rao lower bound over all SNRsshown.
As a result,
εss ≥(p(n− p)(1 + SNR)
)1/2
K1/2SNR(radians), (145)
where the sectional and Riemannian curvature termsK(b) and Rm(C) have been neglected. For large SNR,this expression is well approximated by
(p(n− p)
)1/2×K−1/2SNR−1/2 (radians).
E. SVD-Based Subspace Estimation
Given ann-by-K data matrixZ whose columns are iidrandom vectors, the standard method [16], [27], [38] ofestimating thep-dimensional principal invariant subspace ofZis to compute the (compact) singular value decomposition
UΣVH := Z, (146)
where U is an n-by-n orthogonal matrix,Σ is an n-by-nordered diagonal matrix, andV is a K-by-n matrix withorthonormal columns. Thep-dimensional principal invariantsubspace ofZ is taken to be the span of the firstp columnsof U.
Furthermore, if an estimate is desired of the subspace rep-resented by the matrixY in Eq. (1), and the background noisecovarianceR0 is non-white and known, the simple SVD-basedestimator using the data vectorsz is biased by the principalinvariant subspace ofR0. In this case, a whitened SVD-basedapproach is used, whereby the SVDUΣVH := R− 1
20 Z of the
whitened data matrix is computed, thenY is taken to be the
10–3
10–2
10–1
Su
bsp
ace
RM
SE
(ra
d)
100
100
101
102
103
Sample support / p
Unwhitened SVDWhitened SVDSubspace CRB
Fig. 5. RMSEs of the whitened and unwhitened subspace estimators(Section IV-E) and the CRB of Eq. (143) versus sample support (divided byp)for the estimation problem of Eq. (1) onG5,2. The RMSE of the unwhitenedSVD estimate is the dashed (green) curve, which exceeds the RMSE of thewhitened SVD estimate (dashedblue curve) because of the bias inducedby R0, especially at large sample support. Below these curves is the CRB inthe solid (red) curve. A constant SNR of21 dB and 1000 Monte Carlo trialsare used. Note that, as expected, the RMSE of the whitened SVD estimateapproaches the Cramer-Rao lower bound as the sample support becomes large,i.e., this maximum likelihood estimator is asymptotically efficient.
first p columns ofU, andY = R120 Y. As noted, this is the
maximum likelihood estimate and is therefore asymptoticallyefficient asK →∞ [17], [75].
F. Simulation Results
A Monte Carlo simulation was implemented to compare thesubspace estimation accuracy achieved by the SVD-based es-timation methods described in Section IV-E with the Cramer-Rao bound predicted in Section IV-C. A2-dimensional sub-space inR5 (chosen randomly from the uniform distributionon G5,2) is estimated given a known5-by-5 noise covarianceR0 and an unknown2-by-2 covariance matrixR1 (chosenrandomly from a Wishart distribution,E [R1] = SNR·I, whereSNR is a signal-to-noise ratio that may be varied). OnceR0, R1, Y, and the number of independent snapshotsK arespecified, the CRB is computed from these values as describedin Section IV-C. One thousand (1000) Monte Carlo trials arethen performed, each of which consists of computing a normaln-by-K data matrixZ whose covariance isR2, estimatingYfrom thep-dimensional principal invariant subspace ofZ andthe whitened data matrixR− 1
20 Z, then computing the natural
subspace distance between these estimates andY (using the2-norm of the vector of principal angles, in radians). The resultscomparing the accuracy of the whitened and unwhitened SVDestimators to the CRB are shown in Figures 4 and 5 as both theSNR and the sample supportK vary. As the SNR is varied,the SVD-based method achieves an accuracy that is a smallconstant fraction above the Cramer-Rao lower bound. Becausethe unwhitened SVD estimator is biased byR0, its RMSEerror is higher than the whitened SVD estimator, especially at

SMITH: COVARIANCE, SUBSPACE, INTRINSIC CRAMER-RAO BOUNDS 19
ROSETTA STONE
MANIFOLD M EUCLIDEAN n-SPACE Rn
M manifold Rn Euclideann-spaceθ ∈M point on manifold x ∈ Rn column vectorTθM tangent space Rn Euclideann-spaceT ∗θM cotangent space (Rn)∗ ∼= Rn dual Euclideann-spaceΩ ∈ TθM tangent vector y ∈ Rn column vectorω ∈ T ∗θM cotangent vector η ∈ R1×n 1-by-n row vectorθ(t) curve onM , θ(t) tangent vector x(t) curve inRn, x(t) tangent vector`(θ) ∈ R function onM `(x) ∈ R function onRn
d` ∈ T ∗θM differential of ` ∂`/∂x 1-by-n vector of derivativesd`(Ω) ∈ R directional derivative of ∂`/∂x · y directional derivative ofb(θ) ∈ TθM vector field b(x) ∈ Rn vector fieldφ : M → P differentiable mapping φ(x), φ : Rn → Rp
φ∗ : TθM → Tφ(θ)P push-forward ∂φ/∂x p-by-n Jacobian matrix ofφθ = (θ1, . . . , θn) coordinates onM x = (x1, . . . , xn)T ∈ Rn column vector(∂/∂θ1), . . . , (∂/∂θn) basis ofTθM e1, . . . , en standard basis ofRn
dθ1, . . . , dθn dual basis ofT ∗θM eT1 , . . . , eT
n standard basis ofR1×n
∇ connection/covariant differential ∂(·)/∂x partial differentiation∇Ω covariant derivative ∂(·)/∂x · y directional derivative∇∂/∂θi(∂/∂θj) =
∑k Γk
ij(∂/∂θk) ∂ej/∂x = 0 ⇔ Γk
ij ≡ 0 in flat space∇b : TθM → TθM , ∇b(Ω) = ∇Ωb ∂b/∂x n-by-n Jacobian matrix ofb∇2` 2d covariant differential of ∂2`/∂x2 n-by-n Hessian matrix ofg : TθM × TθM → R Riemannian metric G, xTGx quadratic form onRn
g−1 : T ∗θM × T ∗θM → R inverse metric G−1 inverse quadratic formgij = g(∂/∂θi, ∂/∂θj) metric coefficients (G)ij = eT
i Gej matrix coefficientsgij = g−1(dθi, dθj) inverse coefficients (G−1)ij = eT
i G−1ej inverse coefficients
gfim = E [d`⊗ d`] = −E [∇2`] FIM G = E [(∂`/∂x)T(∂`/∂x)] = −E [∂2`/∂x2]gradθ ` ∈ TθM gradient vector field gradθ ` = G−1(∂`/∂x)T ∈ Rn gradientθ + Γ(θ, θ) = 0 geodesic equation x = 0 geodesic equationΓ : TθM × TθM → TθM Γ ≡ 0 in flat spaceexpθ tΩ ∈M geodesic curve/exponential map x + ty line/vector additionexp−1
θ θ ∈ TθM inverse exponential map x− x vector subtractionτt : TθM → Texp tΩM parallel translation y 7→ y identity map is parallel∇Ωb|t=0 = ∇b(exp tΩ) = b(0) + Γ
(b(0),Ω
)(∂b/∂x)·y = (d/dt)|t=0b(x + ty) = b(0)
∇Ωb|t=0 = limt→0
(τ−1t b(exp tΩ)− b(0)
)/t (∂b/∂x)·y = limt→0
(b(x + ty)− b(0)
)/t
K(X ∧ Y ) = 〈R(X,Y )Y ,X〉/‖X ∧ Y ‖2 sectional curvature K ≡ 0 in flat spaceR(X,Y ) = ∇X∇Y −∇Y ∇X −∇[X,Y ] Riemannian curvature R ≡ 0 in flat space
higher sample support. As the sample support is varied, theaccuracy of the SVD-based method asymptotically approachesthe lower bound, i.e., the SVD method is asymptoticallyefficient.
V. CONCLUSIONS
Covariance matrix and subspace estimation are but twoexamples of estimation problems on manifolds where noset of intrinsic coordinates exists. In this paper biased andunbiased intrinsic Cramer-Rao bounds are derived, alongwith several of their properties, with a view toward sig-nal processing and related applications. Of specific appli-
cability is an expression for the Fisher information metricthat involves the second covariant differential of the log-likelihood function given an arbitrary affine connection, or,equivalently, arbitrary geodesics. These general results are thenapplied to the specific examples of estimating a covariancematrix in the manifoldPn
∼= Gl(n,C)/U(n) of positive-definite matrices, and estimating a subspace in the Grassmannmanifold Gn,p
∼= O(n)/(O(n− p)×O(p)
)in the presence
of an unknown covariance matrix inPp. The CRB of anunbiased covariance matrix estimator using both the naturaland flat (Frobenius) covariance metrics is derived, and shownfor the natural metric to be(10/ log 10)n/K1/2 dB (n-by-n

20 TO APPEAR IN IEEE TRANS. SIGNAL PROCESSING
Hermitian case with sample supportK). It is well known thatwith respect to the flat metric, the sample covariance matrixis an unbiased and efficient estimator, but this metric doesnot quantify the extra loss in estimation accuracy observedat low sample support. Remarkably, the sample covariancematrix is biased and not efficient with respect to the naturalinvariant metric onPn, and the SCM’s bias reveals the extraloss of estimation accuracy at low sample support observedin theory and practice. For this and other geometric reasons(completeness, invariance), the natural invariant metric for thecovariance matrices is recommended over the flat metric foranalysis of covariance matrix estimation.
The CRB of the subspace estimation problem is com-puted in closed-form and compared with the SVD-basedmethod of computing the principal invariant subspace ofa data matrix. In the simplest case, the Cramer-Raobound on subspace estimation accuracy is shown to beabout
(p(n− p)
)1/2K−1/2SNR−1/2 rad for p-dimensional
subspaces. By varying theSNR of the unknown subspace,the RMSE of the SVD-based subspace estimation methodis seen to exceed the CRB by a small constant fraction.Furthermore, the SVD-based subspace estimator is confirmedto be asymptotically efficient, consistent with the fact that itis the maximum likelihood estimate. From these observationswe conclude that the principal invariant subspace can providean excellent estimate of an unknown subspace. In addition tothe examples of covariance matrices and subspaces, the theoryand methods described in this paper are directly applicable tomany other estimation problems on manifolds encountered insignal processing and other applications, such as computingaccuracy bounds on rotation matrices, i.e., the orthogonal orunitary groups, and subspace basis vectors, i.e., the Stiefelmanifold.
Finally, several intriguing open questions are suggested bythe results: What is the geometric significance of the factthat only the SCM’s determinant is biased? Does this fact,along with the numerical results in Section III-C, suggestimproved covariance estimation techniques at low samplesupport? Would any such technique be preferable to the ad hocbut effective method of “diagonal loading”? Is the whitenedSVD a biased subspace estimator? Does the geometry of theGrassmann manifold, akin to the SCM’s biased determinant,have any bearing on subspace bias? Are there important appli-cations where the curvature terms appearing in the Cramer-Raobound are significant? Such questions illustrate the principlethat admitting a problem’s geometry into its analysis not onlyoffers a path to the problem’s solution, but also opens newareas of study.
ACKNOWLEDGMENTS
I benefited enormously in writing this paper from conver-sations with Al Hero and Louis Scharf, and from excellentfeedback from the anonymous reviewers. In particular, Louis’perceptive editorial and pedagogical suggestions greatly im-proved this paper. I am also greatly indebted to Joao Xavier,who helped me to identify an inaccuracy in the draft.
REFERENCES
[1] P.-A. ABSIL, R. MAHONEY, and R. SEPULCHRE. Riemannian geom-etry of Grassmann manifolds with a view on algorithmic computation.Acta Applicandae Mathematicae80(2) : 199–220, January 2004.
[2] R. L. ADLER, J. P. DEDIEU, J. Y. MARGULIES, M. MARTENS, andM. SHUB. Newton’s method on Riemannian manifolds and a geometricmodel for the human spine.IMA J. Numer. Anal.22: 359–390, 2002.
[3] S. AMARI . Differential-Geometrical Methods in Statistics, Lecture Notesin Statistics,28. Berlin: Springer-Verlag, 1985.
[4] . Differential geometric theory of statistics. InDifferential Ge-ometry in Statistical Inference. IMS Lecture Notes—Monograph Series,vol. 10, ed. S. S. GUPTA, Hayward, CA: Institute of MathematicalStatistics, 1987.
[5] . Methods of Information Geometry, Transl. Math. Mon.191(transl. D. HARADA ). Providence, RI: American Mathematical Society,2000. Originally published in Japanese as “Joho kika no hoho” byIwanami Shoten, Publishers, Tokyo, 1993.
[6] . Information geometry on hierarchy of probability distributions.IEEE Trans. Informat. Th.47(5) : 1701–1711, 2001.
[7] W. J. BANGS. Array processing with generalized beamformers. Ph.D.thesis, Yale University, New Haven, CT, 1971.
[8] T. A. BARTON and S. T. SMITH . Structured covariance estimation forspace-time adaptive processing. InProc. 1997 IEEE Conf. Acoust.,Speech, Sig. Proc.(Munich, Germany), 1997.
[9] R. BHATTACHARYA and V. PATRANGENARU. Nonparametric estimationof location and dispersion on Riemannian manifolds.J. StatisticalPlanning and Inference108: 23–35, 2002.
[10] W. M. BOOTHBY. An Introduction to Differential Manifolds and Rie-mannian Geometry, 2d ed. New York: Academic Press, 1986.
[11] D. C. BRODY and L. P. HUGHSTON. Statistical geometry in quantummechanics.Proc. R. Soc. Lond.A 454: 2445–2475, 1998.
[12] I. CHAVEL . Riemannian Geometry—A Modern Introduction. London:Cambridge University Press, 1993.
[13] J. CHEEGER and D. G. EBIN Comparison Theorems in RiemannianGeometry. Amsterdam: North-Holland Publishing Company, 1975.
[14] A. CICHOCKI and S. AMARI . Adaptive Blind Signal and Image Pro-cessing. West Sussex, England: John Wiley and Sons, Ltd. 2002.
[15] A. CICHOCKI and P. GEORGIEV. Blind source separation algorithmswith matrix constraints.IEICE Trans. Informat. Syst.E86-A (1) : 522–531, January 2003.
[16] P. COMON and G. H. GOLUB. Tracking a few extreme singular valuesand vectors in signal processing.Proc. IEEE78(8) : 1327–1343, 1990.
[17] H. CRAMER. Mathematical Methods of Statistics. Princeton, NJ: Prince-ton U. Press, 1946.
[18] P. DIACONIS. Group Representations in Probability and Statistics. IMSLecture Notes—Monograph Series, vol. 11, ed. S. S. GUPTA. Hayward,CA: Institute of Mathematical Statistics, 1988.
[19] S. C. DOUGLAS. Self-stabilized gradient algorithms for blind sourceseparation with orthogonality constraints.IEEE Trans. Neural Networks11(6) : 1490–1497, November 2000.
[20] S. C. DOUGLAS, S. AMARI , and S.-Y. KUNG. On gradient adaptionwith unit-norm constraints.IEEE Trans. Signal Processing48(6) : 1843–1847, June 2000.
[21] A. EDELMAN and S. T. SMITH . On conjugate-gradient-like methodsfor eigen-like problems.BIT 36(3) : 494–508, 1996. See alsoLinearand Nonlinear Conjugate Gradient-Related Methods, eds. L. ADAMS
and J. L. NAZARETH. Philadelphia, PA: SIAM, 1996.[22] A. EDELMAN , T. A. ARIAS, and S. T. SMITH . The geometry of
algorithms with orthogonality constraints.SIAM Matrix Anal. Appl.20(2) : 303–353, 1998.
[23] K.-T. FANG and Y.-T. ZHANG. Generalized Multivariate Analysis.Beijing: Science Press, and Heidelberg: Springer-Verlag, 1990.
[24] J. FARAUT and A. KORANYI . Analysis On Symmetric Cones. London:Oxford University Press, 1994.
[25] R. A. FISHER. On the mathematical foundations of theoreti-cal statistics. Phil. Trans. Roy. Soc.A 222: 309–368, 1922. Seealso http://www.library.adelaide.edu.au/digitised/fisher/18pt1.pdf .
[26] . Dispersion on a sphere.Proc. Roy. Soc. LondonA 217(1130) :295–305, 1953.
[27] G. H. GOLUB and C. VAN LOAN. Matrix Computations, 3d ed.Baltimore, MD: Johns Hopkins University Press, 1996.
[28] J. D. GORMAN and A. O. HERO. Lower bounds for parametric esti-mation with constraints.IEEE Trans. Informat. Th.26(6) : 1285–1301,November 1990.

SMITH: COVARIANCE, SUBSPACE, INTRINSIC CRAMER-RAO BOUNDS 21
[29] U. GRENANDER, M. M ILLER, and A. SRIVASTAVA . Hilbert-Schmidtlower bounds for estimators on matrix Lie groups for ATR.IEEE Trans.Patt. Anal. Machine Intell.20: 790–802, August 1998.
[30] S. HELGASON. Differential Geometry, Lie Groups, and SymmetricSpaces. New York: Academic Press, 1978.
[31] . Groups and Geometric Analysis. New York: Academic Press,1984.
[32] U. HELMKE and J. B. MOORE. Optimization and Dynamical Systems.Berlin: Springer-Verlag, 1994.
[33] H. HENDRIKS. A Cramer-Rao type lower bound for estimators withvalues on a manifold.J. Multivariate Anal.38: 245–261, 1991.
[34] B. M. HOCHWALD and T. L. MARZETTA. Unitary space-time modula-tion for multiple-antenna communications in Rayleigh flat fading.IEEETrans. Informat. Th.46(2) : 543–564, March 2002.
[35] I. M. JOHNSTONE. On the distribution of the largest eigenvalue inprincipal components analysis.Ann. Stat.29(2) : 295–327, 2001.
[36] H. KARCHER. Riemannian center of mass and mollifier smoothing.Comm. Pure Appl. Math.30: 509–541, 1977.
[37] S. KOBAYASHI and K. NOMIZU. Foundations of Differential Geometry,vols. 1 and 2. New York: Interscience Publishers, 1969.
[38] E. LUNDSTROM and L. ELDEN. Adaptive eigenvalue computationsusing Newton’s method on the Grassmann manifold.SIAM Matrix Anal.Appl. 23(3) : 819–839, 2002.
[39] Y. M A, J. KOSECKA, and S. SASTRY. Optimization criteria and geo-metric algorithms for motion and structure estimation.Intl. J. ComputerVision 44(3) : 219–249, 2001.
[40] V. A. M ARCENKO and L. A. PASTUR. Distribution of eigenvalues forsome sets of random matrices.Math. USSR-Sb1 : 457–483, 1967.
[41] K. V. M ARDIA and P. E. JUPP. Directional Statistics. West Sussex,England: John Wiley and Sons, Ltd. 2000.
[42] P. MCCULLAGH . Tensor Methods in Statistics. London: Chapmanand Hall, 1987.
[43] T. MCWHORTER and L. L. SCHARF. Cramer-Rao bounds for determin-istic modal analysis.IEEE Trans. Signal Processing41(5) : 1847–1866,May 1993.
[44] M. L. M ENENDEZ, D. MORALES, L. PARDO, and M. SALICRU.Statistical tests based on geodesic differences.Appl. Math. Lett.8 (1) :65–69, 1995.
[45] R. J. MUIRHEAD. Aspects of Multivariate Statistical Theory. New York:John Wiley and Sons, Inc. 1982.
[46] M. K. M URRAY and J. W. RICE. Differential Geometry and Statistics.London: Chapman and Hall, 1993.
[47] F. D. NEESER and J. L. MASSEY. Proper complex random processeswith applications to information theory.IEEE Trans. Informat. Th.39(7) : 1293–1302, July 1993.
[48] A. OHARA, N. SUDA, and S. AMARI . Dualistic differential geometry ofpositive definite matrices and its applications to related problems.Lin.Alg. Appl.247: 31–53, 1996.
[49] J. M. OLLER. On an intrinsic bias measure. InStability Problems forStochastic Models,Lecture Notes in Mathematics 1546, eds. V. V.KALASHNIKOV and V. M. ZOLOTAREV, Suzdal, Russia, 134–158.Berlin: Springer-Verlag, 1991.
[50] J. M. OLLER and J. M. CORCUERA. Intrinsic analysis of statisticalestimation.Ann. Stat.23(5) : 1562–1581, October 1995.
[51] D. PETZ. Covariance and Fisher information in quantum mechanics.J.Phys.A: Math. Gen.35: 929–939, 1995.
[52] K. RAHBAR and J. P. REILLY . Blind source separation algorithm forMIMO convolutive mixtures. InProc. 3d Intl. Conf. Indep. ComponentAnal. Signal Separation(San Diego, CA, USA), pp. 242–247, December2001.
[53] C. R. RAO. Information and the accuracy attainable in the estimation ofstatistical parameters.Bull. Calcutta Math. Soc.37: 81–89, 1945. SeealsoSelected Papers of C. R. Rao, ed. S. DAS GUPTA, New York: JohnWiley and Sons, Inc. 1994.
[54] . Differential metrics in probability spaces. InDifferential Ge-ometry in Statistical Inference. IMS Lecture Notes—Monograph Series,vol. 10, ed. S. S. GUPTA. Hayward, CA: Institute of MathematicalStatistics, 1987.
[55] I. S. REED, J. D. MALLETT , and L. E. BRENNAN. Rapid conver-gence rate in adaptive arrays.IEEE Trans. Aerospace Electronic Syst.AES-10(6) : 853–863, 1974.
[56] M. J. D. RENDAS and J. M. F. MOURA. Ambiguity in radar and sonar.IEEE Trans. Signal Processing46(2) : 294–305, February 1998.
[57] L. L. SCHARF. Statistical Signal Processing: Detection, Estimation, andTime Series Analysis. Reading, MA: Addison-Wesley Co., 1991.
[58] L. L. SCHARF and T. MCWHORTER. Geometry of the Cramer-Raobound.Signal Processing31: 301–311, 1993.
[59] J. W. SILVERSTEIN. The smallest eigenvalue of a large-dimensionalWishart matrix.Ann. Prob.13: 1364–1368, 1985.
[60] J. W. SILVERSTEIN and Z. D. BAI . On the empirical distributionof eigenvalues of a class of large dimensional random matrices.J.Multivariate Anal.54: 175–192, 1995.
[61] L.T. SKOVGAARD. A Riemannian geometry of the multivariate normalmodel.Scand. J. Stat.11: 211–223, 1984.
[62] S. T. SMITH . Dynamical systems that perform the singular valuedecomposition.Syst. Control Lett.16: 319–327, 1991.
[63] . Subspace tracking with full rank updates. InProc. 31st Asilo-mar Conf. Signals, Systems, Computers, vol. 1, 1997, pp. 793–797.
[64] . Adaptive radar. InWiley Encyclopedia of Electrical andElectronics Engineering, ed. J. G. WEBSTER. Vol. 1, pp. 263–289.New York: John Wiley and Sons, Inc. 1999.
[65] . Intrinsic Cramer-Rao bounds and subspace estimation accu-racy. In Proc. IEEE Sensor Array and Multichannel Signal ProcessingWorkshop(Cambridge, MA), pp. 489–493, 2000.
[66] M. SPIVAK . A Comprehensive Introduction to Differential Geometry,3d ed., vols. 1, 2. Houston, TX: Publish or Perish, Inc., 1999.
[67] A. SRIVASTAVA . A Bayesian approach to geometric subspace estima-tion. IEEE Trans. Signal Processing48(5) : 1390–1400, May 2002.
[68] A. SRIVASTAVA and E. KLASSEN. Monte Carlo extrinsic estimatorsfor manifold-valued parameters.IEEE Trans. Signal Processing50(2) :299–308, February 2002.
[69] . Bayesian, geometric subspace tracking.Advances Appl. Prob.,to appear.
[70] P. STOICA and A. NEHORAI. MUSIC, maximum likelihood, andCramer-Rao bound.IEEE Trans. Acoust., Speech, Signal Processing37(5) : 720–741, May 1989.
[71] . Performance study of conditional and unconditional direction-of-arrival estimation.IEEE Trans. Acoust., Speech, Signal Processing38(10) : 1783–1795, October 1990.
[72] P. STOICA and B. C. NG. On the Cramer-Rao bound under parametricconstraints.IEEE Signal Proc. Lett.5 (7) : 177–179, July 1998.
[73] P. STOICA and T. SODERSTROM. Statistical analysis of MUSIC andsubspace rotation estimates of sinusoidal frequencies.IEEE Trans.Signal Processing39(8) : 1836–1847, August 1991.
[74] R. J. VACCARO and Y. DING. Optimal subspace-based parameterestimation. In Proc. 1993 IEEE Conf. Acoust., Speech, Sig. Proc.(Minneapolis MN, USA), vol. 4, pp. 368–371, 1993.
[75] H. L. VAN TREES. Detection, Estimation, and Modulation Theory,Part 1. New York: John Wiley and Sons, Inc. 1968.
[76] J. XAVIER. Blind identification of MIMO channels based on 2nd orderstatistics and colored inputs. Ph.D. thesis, Instituto Superior Tecnico,Lisbon, Portugal, 2002.
[77] . Geodesic lower bound for parametric estimation with con-straints. InProc. Fifth IEEE Workshop Sig. Proc. Adv. Wireless Comm.(Lisbon, Portugal), July 2004.
[78] R. YANG and J. O. BERGER. Estimation of a covariance matrix usingthe reference prior.Ann. Stat.22(3) : 1195–1211, 1994.
[79] L. ZHENG and D. N. C. TSE. Communication on the Grassmannmanifold: A geometric approach to the noncoherent multiple-antennachannel.IEEE Trans. Informat. Th.48(2) : 359–383, February 2002.
Steven Thomas Smithwas born in La Jolla, CA in1963. He received the B.A.Sc. degree in electricalengineering and mathematics from the University ofBritish Columbia, Vancouver, BC in 1986 and thePh.D. degree in applied mathematics from HarvardUniversity, Cambridge, MA in 1993. From 1986 to1988 he was a research engineer at ERIM, AnnArbor, MI, where he developed morphological imageprocessing algorithms. He is currently a senior mem-ber of the technical staff at MIT Lincoln Laboratory,which he joined in 1993. His research involves
algorithms for adaptive signal processing, detection, and tracking to enhanceradar and sonar systems performance. He has taught signal processing coursesat Harvard and for the IEEE. His most recent work addresses intrinsicestimation and superresolution bounds, mean and variance CFAR, advancedtracking methods, and space-time adaptive processing algorithms. He was anassociate editor of theIEEE Transactions on Signal Processing(2000–2002),and received the SIAM outstanding paper award in 2001.


![Cramer John[1]](https://static.fdocuments.us/doc/165x107/577cc5861a28aba7119cae23/cramer-john1.jpg)








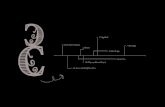







![Cramer-Krasselt [Encyclopedia Entry]](https://static.fdocuments.us/doc/165x107/6287a080880e1f62332902cc/cramer-krasselt-encyclopedia-entry.jpg)