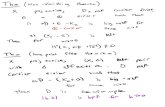Projective Geometry and Pappus' Theorem - Department of
Transcript of Projective Geometry and Pappus' Theorem - Department of

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry and Pappus’ Theorem
Kelly McKinnie
March 23, 2010

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria
Pappus of Alexandria was a Greek mathematician.
He lived around the time of the 3rd century AD.
Appears to have witnessed a solar eclipse in 320 AD, butthere is some confusion about this.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria
Pappus of Alexandria was a Greek mathematician.
He lived around the time of the 3rd century AD.
Appears to have witnessed a solar eclipse in 320 AD, butthere is some confusion about this.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria
Pappus of Alexandria was a Greek mathematician.
He lived around the time of the 3rd century AD.
Appears to have witnessed a solar eclipse in 320 AD, butthere is some confusion about this.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria
Pappus of Alexandria was a Greek mathematician.
He lived around the time of the 3rd century AD.
Appears to have witnessed a solar eclipse in 320 AD, butthere is some confusion about this.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Mathematical contributions
His major contribution is a book called Synagoge, also knownas “Mathematical Collections”.
The Mathematical Collections of Pappus in a translation ofFederico Commandino (1589).

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Mathematical contributions
His major contribution is a book called Synagoge, also knownas “Mathematical Collections”.
The Mathematical Collections of Pappus in a translation ofFederico Commandino (1589).

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Mathematical contributions
His major contribution is a book called Synagoge, also knownas “Mathematical Collections”.
The Mathematical Collections of Pappus in a translation ofFederico Commandino (1589).

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Vatican Exhibit of Pappus’ Collections

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Vatican Exhibit of Pappus’ Collections
Caption on the exhibit:
“Pappus’s “Collection,” consisting of supplements to earliertreatises on geometry, astronomy, and mechanics, dates fromthe late third century A.D. and is the last important work ofGreek mathematics. This manuscript reached the papal libraryin the thirteenth century, and is the archetype of all latercopies, of which none is earlier than the sixteenth century. ”
Courtesy of http://www.ibiblio.org

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Vatican Exhibit of Pappus’ Collections
Caption on the exhibit:
“Pappus’s “Collection,” consisting of supplements to earliertreatises on geometry, astronomy, and mechanics, dates fromthe late third century A.D. and is the last important work ofGreek mathematics. This manuscript reached the papal libraryin the thirteenth century, and is the archetype of all latercopies, of which none is earlier than the sixteenth century. ”
Courtesy of http://www.ibiblio.org

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
One piece of mathematics in ”Collection” is a seeminglyoriginal theorem that has since become known as Pappus’Theorem.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
Let three points A, B, C be incident to a single straight line
AB
C

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
Let three points A, B, C be incident to a single straight line
AB
C

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
Let three points A, B, C be incident to a single straight lineand another three points A′, B ′, C ′ incident to another straightline.
AB
C
A' B' C'

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
Let three points A, B, C be incident to a single straight lineand another three points A′, B ′, C ′ incident to another straightline. Then the three pairwise intersections AB ′ ∩ A′B
AB
C
A' B' C'

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
Let three points A, B, C be incident to a single straight lineand another three points A′, B ′, C ′ incident to another straightline. Then the three pairwise intersections AB ′ ∩ A′B,AC ′ ∩ A′C
AB
C
A' B' C'

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
Let three points A, B, C be incident to a single straight lineand another three points A′, B ′, C ′ incident to another straightline. Then the three pairwise intersections AB ′ ∩ A′B,AC ′ ∩ A′C and BC ′ ∩ B ′C
AB
C
A' B' C'

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
Let three points A, B, C be incident to a single straight lineand another three points A′, B ′, C ′ incident to another straightline. Then the three pairwise intersections AB ′ ∩ A′B,BC ′ ∩ C ′B and AC ′ ∩ A′C are incident to a third straight line.
AB
C
A' B' C'

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
Let three points A, B, C be incident to a single straight lineand another three points A′, B ′, C ′ incident to another straightline. Then the three pairwise intersections AB ′ ∩ A′B,BC ′ ∩ C ′B and AC ′ ∩ A′C are incident to a third straight line.
AB
C
A' B' C'

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
Java Applet on the web athttp://www.cut-the-knot.org/pythagoras/Pappus.shtml

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
As you can see from the Java Applet, Pappus’ Theorem shouldreally read:
Let three points A, B, C be incident to a singlestraight line and another three points A′, B ′, C ′ incident to(generally speaking) another straight line. Then the threepairwise intersections AB ′ ∩ A′B, BC ′ ∩ C ′B and AC ′ ∩ A′Care incident to a third straight line.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
As you can see from the Java Applet, Pappus’ Theorem shouldreally read: Let three points A, B, C be incident to a singlestraight line and another three points A′, B ′, C ′ incident to
(generally speaking) another straight line. Then the threepairwise intersections AB ′ ∩ A′B, BC ′ ∩ C ′B and AC ′ ∩ A′Care incident to a third straight line.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
As you can see from the Java Applet, Pappus’ Theorem shouldreally read: Let three points A, B, C be incident to a singlestraight line and another three points A′, B ′, C ′ incident to(generally speaking)
another straight line. Then the threepairwise intersections AB ′ ∩ A′B, BC ′ ∩ C ′B and AC ′ ∩ A′Care incident to a third straight line.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
As you can see from the Java Applet, Pappus’ Theorem shouldreally read: Let three points A, B, C be incident to a singlestraight line and another three points A′, B ′, C ′ incident to(generally speaking) another straight line. Then the threepairwise intersections AB ′ ∩ A′B, BC ′ ∩ C ′B and AC ′ ∩ A′Care incident to a third straight line.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
As you can see from the Java Applet, Pappus’ Theorem shouldreally read: Let three points A, B, C be incident to a singlestraight line and another three points A′, B ′, C ′ incident to(generally speaking) another straight line. Then the threepairwise intersections AB ′ ∩ A′B, BC ′ ∩ C ′B and AC ′ ∩ A′Care incident to a third straight line.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
i.e., in Euclidean Geometry we shouldn’t allow the points A′,B ′, C ′ to be in the configuration
AB
C
A' B' C'

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Pappus of Alexandria - Pappus’ Theorem
i.e., in Euclidean Geometry we shouldn’t allow the points A′,B ′, C ′ to be in the configuration
AB
C
A' B' C'

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
We would like to put Pappus’ Theorem in a setting where wedon’t have to make lots of EXCEPTIONS for certainconfigurations.
We need a new “geometry” in which EVERY non-equal pair oflines meets in exactly one point.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
We would like to put Pappus’ Theorem in a setting where wedon’t have to make lots of EXCEPTIONS for certainconfigurations.We need a new “geometry” in which EVERY non-equal pair oflines meets in exactly one point.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Euclidean Geometry - Review
Recall in 2-dimensional (plane) Euclidean geometry, every pointis given by a pair (x , y) with x and y ∈ R.
How do we describe a line in the Euclidean plane?They are the points that are the solutions to
y = mx + b
for fixed m and b ∈ R,or solutions to
x = a
for a fixed a ∈ R.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Euclidean Geometry - Review
Recall in 2-dimensional (plane) Euclidean geometry, every pointis given by a pair (x , y) with x and y ∈ R.
How do we describe a line in the Euclidean plane?They are the points that are the solutions to
y = mx + b
for fixed m and b ∈ R,or solutions to
x = a
for a fixed a ∈ R.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Euclidean Geometry - Review
Recall in 2-dimensional (plane) Euclidean geometry, every pointis given by a pair (x , y) with x and y ∈ R.
How do we describe a line in the Euclidean plane?
They are the points that are the solutions to
y = mx + b
for fixed m and b ∈ R,or solutions to
x = a
for a fixed a ∈ R.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Euclidean Geometry - Review
Recall in 2-dimensional (plane) Euclidean geometry, every pointis given by a pair (x , y) with x and y ∈ R.
How do we describe a line in the Euclidean plane?They are the points that are the solutions to
y = mx + b
for fixed m and b ∈ R,or solutions to
x = a
for a fixed a ∈ R.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Euclidean Geometry - Review
Recall in 2-dimensional (plane) Euclidean geometry, every pointis given by a pair (x , y) with x and y ∈ R.
How do we describe a line in the Euclidean plane?They are the points that are the solutions to
y = mx + b
for fixed m and b ∈ R,
or solutions to
x = a
for a fixed a ∈ R.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Euclidean Geometry - Review
Recall in 2-dimensional (plane) Euclidean geometry, every pointis given by a pair (x , y) with x and y ∈ R.
How do we describe a line in the Euclidean plane?They are the points that are the solutions to
y = mx + b
for fixed m and b ∈ R,or solutions to
x = a
for a fixed a ∈ R.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Euclidean Geometry - Review
Recall in 2-dimensional (plane) Euclidean geometry, every pointis given by a pair (x , y) with x and y ∈ R.
How do we describe a line in the Euclidean plane?They are the points that are the solutions to
y = mx + b
for fixed m and b ∈ R,or solutions to
x = a
for a fixed a ∈ R.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Euclidean Geometry - Review
Two linesy = m1x + b1
andy = m2x + b2
intersect if there is a solution
m1x + b1 = m2x + b2
(m1 −m2)x = b2 − b1
x =b2 − b1
m1 −m2
i.e., we need m1 6= m2 in order for there to exist a point ofintersection.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Euclidean Geometry - Review
Two lines
y = m1x + b1
andy = m2x + b2
intersect if there is a solution
m1x + b1 = m2x + b2
(m1 −m2)x = b2 − b1
x =b2 − b1
m1 −m2
i.e., we need m1 6= m2 in order for there to exist a point ofintersection.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Euclidean Geometry - Review
Two linesy = m1x + b1
andy = m2x + b2
intersect if there is a solution
m1x + b1 = m2x + b2
(m1 −m2)x = b2 − b1
x =b2 − b1
m1 −m2
i.e., we need m1 6= m2 in order for there to exist a point ofintersection.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Euclidean Geometry - Review
Two linesy = m1x + b1
andy = m2x + b2
intersect if there is a solution
m1x + b1 = m2x + b2
(m1 −m2)x = b2 − b1
x =b2 − b1
m1 −m2
i.e., we need m1 6= m2 in order for there to exist a point ofintersection.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Euclidean Geometry - Review
Two linesy = m1x + b1
andy = m2x + b2
intersect if there is a solution
m1x + b1 = m2x + b2
(m1 −m2)x = b2 − b1
x =b2 − b1
m1 −m2
i.e., we need m1 6= m2 in order for there to exist a point ofintersection.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Euclidean Geometry - Review
Two linesy = m1x + b1
andy = m2x + b2
intersect if there is a solution
m1x + b1 = m2x + b2
(m1 −m2)x = b2 − b1
x =b2 − b1
m1 −m2
i.e., we need m1 6= m2 in order for there to exist a point ofintersection.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Euclidean Geometry - Review
Two linesy = m1x + b1
andy = m2x + b2
intersect if there is a solution
m1x + b1 = m2x + b2
(m1 −m2)x = b2 − b1
x =b2 − b1
m1 −m2
i.e., we need m1 6= m2 in order for there to exist a point ofintersection.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
We want to fix this “flaw” of Euclidean geometry.
We wantevery pair of distinct lines to intersect in exactly one point.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
We want to fix this “flaw” of Euclidean geometry. We wantevery pair of distinct lines to intersect in exactly one point.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
Where else have people noted a need for “extra” points?
Inperspective drawing in art.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
Where else have people noted a need for “extra” points? Inperspective drawing in art.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
The point on the horizon that looks like the intersection of theparallel lines is called an ideal point.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
Satire on false perspective by William Hogarth.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
To make the new geometry we need to decide:
What are the points of the new geometry?
We want to incorporate all of the Euclidean points into ourprojective geometry.
What are the lines of the new geometry?
We want to incorporate our old lines into our new ones.We want all of our new lines to intersect in exactly onepoint.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
To make the new geometry we need to decide:
What are the points of the new geometry?
We want to incorporate all of the Euclidean points into ourprojective geometry.
What are the lines of the new geometry?
We want to incorporate our old lines into our new ones.We want all of our new lines to intersect in exactly onepoint.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
To make the new geometry we need to decide:
What are the points of the new geometry?
We want to incorporate all of the Euclidean points into ourprojective geometry.
What are the lines of the new geometry?
We want to incorporate our old lines into our new ones.We want all of our new lines to intersect in exactly onepoint.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
To make the new geometry we need to decide:
What are the points of the new geometry?
We want to incorporate all of the Euclidean points into ourprojective geometry.
What are the lines of the new geometry?
We want to incorporate our old lines into our new ones.We want all of our new lines to intersect in exactly onepoint.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
To make the new geometry we need to decide:
What are the points of the new geometry?
We want to incorporate all of the Euclidean points into ourprojective geometry.
What are the lines of the new geometry?
We want to incorporate our old lines into our new ones.
We want all of our new lines to intersect in exactly onepoint.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
To make the new geometry we need to decide:
What are the points of the new geometry?
We want to incorporate all of the Euclidean points into ourprojective geometry.
What are the lines of the new geometry?
We want to incorporate our old lines into our new ones.We want all of our new lines to intersect in exactly onepoint.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
We don’t want to add more points than we need.
What wereally need is a new point for every SLOPE in the Euclideanplane. Then we can say that two parallel lines intersect at thisnew point, the point that corresponds to their slope.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
We don’t want to add more points than we need. What wereally need is a new point for every SLOPE in the Euclideanplane. Then we can say that two parallel lines intersect at thisnew point, the point that corresponds to their slope.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
New Point!

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
New point!

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry
How do we do this concretely?

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - points
Definition
A point in the projective plane is given by a TRIPLE [x , y , z ]with x , y , z ∈ R
such that
not all x = 0, y = 0 and z = 0, and
two points [x1, y1, z1] and [x2, y2, z2] are equivalent if thereis a scalar λ ∈ R− {0} such that
λ[x1, y1, z1] = [x2, y2, z2].
The symbol for the projective plane is RP2.
For example, in the projective plane,
[1, 2, 3] = [5, 10, 15] and [2, 2, 2] = [3, 3, 3].
[0, 0, 0] is not a point in the projective plane!

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - points
Definition
A point in the projective plane is given by a TRIPLE [x , y , z ]with x , y , z ∈ R such that
not all x = 0, y = 0 and z = 0, and
two points [x1, y1, z1] and [x2, y2, z2] are equivalent if thereis a scalar λ ∈ R− {0} such that
λ[x1, y1, z1] = [x2, y2, z2].
The symbol for the projective plane is RP2.
For example, in the projective plane,
[1, 2, 3] = [5, 10, 15] and [2, 2, 2] = [3, 3, 3].
[0, 0, 0] is not a point in the projective plane!

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - points
Definition
A point in the projective plane is given by a TRIPLE [x , y , z ]with x , y , z ∈ R such that
not all x = 0, y = 0 and z = 0, and
two points [x1, y1, z1] and [x2, y2, z2] are equivalent if thereis a scalar λ ∈ R− {0} such that
λ[x1, y1, z1] = [x2, y2, z2].
The symbol for the projective plane is RP2.
For example, in the projective plane,
[1, 2, 3] = [5, 10, 15] and [2, 2, 2] = [3, 3, 3].
[0, 0, 0] is not a point in the projective plane!

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - points
Definition
A point in the projective plane is given by a TRIPLE [x , y , z ]with x , y , z ∈ R such that
not all x = 0, y = 0 and z = 0, and
two points [x1, y1, z1] and [x2, y2, z2] are equivalent if thereis a scalar λ ∈ R− {0} such that
λ[x1, y1, z1] = [x2, y2, z2].
The symbol for the projective plane is RP2.
For example, in the projective plane,
[1, 2, 3] = [5, 10, 15] and [2, 2, 2] = [3, 3, 3].
[0, 0, 0] is not a point in the projective plane!

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - points
Definition
A point in the projective plane is given by a TRIPLE [x , y , z ]with x , y , z ∈ R such that
not all x = 0, y = 0 and z = 0, and
two points [x1, y1, z1] and [x2, y2, z2] are equivalent if thereis a scalar λ ∈ R− {0} such that
λ[x1, y1, z1] = [x2, y2, z2].
The symbol for the projective plane is RP2.
For example, in the projective plane,
[1, 2, 3] = [5, 10, 15] and [2, 2, 2] = [3, 3, 3].
[0, 0, 0] is not a point in the projective plane!

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - points
Definition
A point in the projective plane is given by a TRIPLE [x , y , z ]with x , y , z ∈ R such that
not all x = 0, y = 0 and z = 0, and
two points [x1, y1, z1] and [x2, y2, z2] are equivalent if thereis a scalar λ ∈ R− {0} such that
λ[x1, y1, z1] = [x2, y2, z2].
The symbol for the projective plane is RP2.
For example, in the projective plane,
[1, 2, 3] = [5, 10, 15] and [2, 2, 2] = [3, 3, 3].
[0, 0, 0] is not a point in the projective plane!

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - points
Definition
A point in the projective plane is given by a TRIPLE [x , y , z ]with x , y , z ∈ R such that
not all x = 0, y = 0 and z = 0, and
two points [x1, y1, z1] and [x2, y2, z2] are equivalent if thereis a scalar λ ∈ R− {0} such that
λ[x1, y1, z1] = [x2, y2, z2].
The symbol for the projective plane is RP2.
For example, in the projective plane,
[1, 2, 3] = [5, 10, 15] and [2, 2, 2] = [3, 3, 3].
[0, 0, 0] is not a point in the projective plane!

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - points
Definition
A point in the projective plane is given by a TRIPLE [x , y , z ]with x , y , z ∈ R such that
not all x = 0, y = 0 and z = 0, and
two points [x1, y1, z1] and [x2, y2, z2] are equivalent if thereis a scalar λ ∈ R− {0} such that
λ[x1, y1, z1] = [x2, y2, z2].
The symbol for the projective plane is RP2.
For example, in the projective plane,
[1, 2, 3] = [5, 10, 15] and [2, 2, 2] = [3, 3, 3].
[0, 0, 0] is not a point in the projective plane!

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - points
In other words, a point of the projective plane [x , y , z ]corresponds to all points on the line through the origincontaining the point (x , y , z) in Euclidean 3-space (R3) exceptthe origin.
(x, y, z)
k(x,y,z)
The red line is all scalar multiplies of (x,y,z)

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
The projective plane
x
y
z

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
The projective plane
x
y
z

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
The projective plane
x
y
z

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
The projective plane
x
y
z

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - points
How does the Euclidean plane “fit into” the projective plane?
The Euclidean point (x , y) is the point [x , y , 1] in RP2.Every point [x , y , z ] ∈ RP2 with z 6= 0 is equivalent to
[x
z,y
z, 1].

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - points
How does the Euclidean plane “fit into” the projective plane?The Euclidean point (x , y) is the point [x , y , 1] in RP2.
Every point [x , y , z ] ∈ RP2 with z 6= 0 is equivalent to
[x
z,y
z, 1].

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - points
How does the Euclidean plane “fit into” the projective plane?The Euclidean point (x , y) is the point [x , y , 1] in RP2.Every point [x , y , z ] ∈ RP2 with z 6= 0 is equivalent to
[x
z,y
z, 1].

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - points
(x/z, y/z, 1)
(x, y, z)

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - points
So the only “new points” we are adding are those with thethird coordinate z = 0.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
A line in RP2 is given by the solutions to
Ax + By + Cz = 0
for some A, B, C ∈ R, not all zero.
Since we have many representations for one point, we need tocheck that this makes sense!

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
A line in RP2 is given by the solutions to
Ax + By + Cz = 0
for some A, B, C ∈ R, not all zero.Since we have many representations for one point, we need tocheck that this makes sense!

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
If the point [x0, y0, z0] satisfies Ax + By + Cz = 0, doesλ[x0, y0, z0] = [λx0, λy0, λz0] also satisfy the equation?
Aλx0 + Bλy0 + Cλz0 = λ(Ax0 + By0 + Cz0)
= λ(0)
= 0
So the equation of the line is well defined.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
If the point [x0, y0, z0] satisfies Ax + By + Cz = 0, doesλ[x0, y0, z0] = [λx0, λy0, λz0] also satisfy the equation?
Aλx0 + Bλy0 + Cλz0 =
λ(Ax0 + By0 + Cz0)
= λ(0)
= 0
So the equation of the line is well defined.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
If the point [x0, y0, z0] satisfies Ax + By + Cz = 0, doesλ[x0, y0, z0] = [λx0, λy0, λz0] also satisfy the equation?
Aλx0 + Bλy0 + Cλz0 = λ(Ax0 + By0 + Cz0)
= λ(0)
= 0
So the equation of the line is well defined.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
If the point [x0, y0, z0] satisfies Ax + By + Cz = 0, doesλ[x0, y0, z0] = [λx0, λy0, λz0] also satisfy the equation?
Aλx0 + Bλy0 + Cλz0 = λ(Ax0 + By0 + Cz0)
= λ(0)
= 0
So the equation of the line is well defined.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
If the point [x0, y0, z0] satisfies Ax + By + Cz = 0, doesλ[x0, y0, z0] = [λx0, λy0, λz0] also satisfy the equation?
Aλx0 + Bλy0 + Cλz0 = λ(Ax0 + By0 + Cz0)
= λ(0)
= 0
So the equation of the line is well defined.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
If the point [x0, y0, z0] satisfies Ax + By + Cz = 0, doesλ[x0, y0, z0] = [λx0, λy0, λz0] also satisfy the equation?
Aλx0 + Bλy0 + Cλz0 = λ(Ax0 + By0 + Cz0)
= λ(0)
= 0
So the equation of the line is well defined.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
You can see the Euclidean lines by setting z = 1:
Ax + By + Cz = 0 − Projective line
Ax + By + C = 0 − Euclidean line
As long as B 6= 0, the Euclidean line has slope m = −A/B.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
You can see the Euclidean lines by setting z = 1:
Ax + By + Cz = 0 − Projective line
Ax + By + C = 0 − Euclidean line
As long as B 6= 0, the Euclidean line has slope m = −A/B.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
You can see the Euclidean lines by setting z = 1:
Ax + By + Cz = 0 − Projective line
Ax + By + C = 0 − Euclidean line
As long as B 6= 0, the Euclidean line has slope
m = −A/B.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
You can see the Euclidean lines by setting z = 1:
Ax + By + Cz = 0 − Projective line
Ax + By + C = 0 − Euclidean line
As long as B 6= 0, the Euclidean line has slope m = −A/B.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
In projective geometry the line given by z = 0 is called the lineat infinity.
The points on the line at infinity are of the form[x , y , 0] with not both x = 0 and y = 0.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
In projective geometry the line given by z = 0 is called the lineat infinity. The points on the line at infinity are of the form[x , y , 0] with not both x = 0 and y = 0.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
Let’s compute some intersections.
What is
{Line at ∞} ∩ {line given by Ax+By+Cz = 0 with B 6= 0}?
{[x , y , 0]} ∩ {[x , y , z ] |Ax + By + Cz = 0}
= {[x , y , 0] |Ax + By = 0}
= {[x , y , 0] | y = −A
Bx}
= {[x ,−A
Bx , 0]}
= [1,−A
B, 0]

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
Let’s compute some intersections. What is
{Line at ∞} ∩ {line given by Ax+By+Cz = 0 with B 6= 0}?
{[x , y , 0]} ∩ {[x , y , z ] |Ax + By + Cz = 0}
= {[x , y , 0] |Ax + By = 0}
= {[x , y , 0] | y = −A
Bx}
= {[x ,−A
Bx , 0]}
= [1,−A
B, 0]

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
Let’s compute some intersections. What is
{Line at ∞} ∩ {line given by Ax+By+Cz = 0 with B 6= 0}?
{[x , y , 0]} ∩ {[x , y , z ] |Ax + By + Cz = 0}
= {[x , y , 0] |Ax + By = 0}
= {[x , y , 0] | y = −A
Bx}
= {[x ,−A
Bx , 0]}
= [1,−A
B, 0]

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
Let’s compute some intersections. What is
{Line at ∞} ∩ {line given by Ax+By+Cz = 0 with B 6= 0}?
{[x , y , 0]} ∩ {[x , y , z ] |Ax + By + Cz = 0}
= {[x , y , 0] |Ax + By = 0}
= {[x , y , 0] | y = −A
Bx}
= {[x ,−A
Bx , 0]}
= [1,−A
B, 0]

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
Let’s compute some intersections. What is
{Line at ∞} ∩ {line given by Ax+By+Cz = 0 with B 6= 0}?
{[x , y , 0]} ∩ {[x , y , z ] |Ax + By + Cz = 0}
= {[x , y , 0] |Ax + By = 0}
= {[x , y , 0] | y = −A
Bx}
= {[x ,−A
Bx , 0]}
= [1,−A
B, 0]

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
Let’s compute some intersections. What is
{Line at ∞} ∩ {line given by Ax+By+Cz = 0 with B 6= 0}?
{[x , y , 0]} ∩ {[x , y , z ] |Ax + By + Cz = 0}
= {[x , y , 0] |Ax + By = 0}
= {[x , y , 0] | y = −A
Bx}
= {[x ,−A
Bx , 0]}
= [1,−A
B, 0]

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
Let’s compute some intersections. What is
{Line at ∞} ∩ {line given by Ax+By+Cz = 0 with B 6= 0}?
{[x , y , 0]} ∩ {[x , y , z ] |Ax + By + Cz = 0}
= {[x , y , 0] |Ax + By = 0}
= {[x , y , 0] | y = −A
Bx}
= {[x ,−A
Bx , 0]}
= [1,−A
B, 0]

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
The line Ax + By + Cz = 0 and the line at infinity intersect atthe point [1,m, 0] corresponding to the slope m = −A/B ofthe Euclidean line Ax + By + C = 0.
In particular, any two distinct parallel lines with slope m(m 6=∞) intersect at the line at infinity at the projective point[1,m, 0].
You an check that all vertical lines intersect at the projectivepoint [0, 1, 0].

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
The line Ax + By + Cz = 0 and the line at infinity intersect atthe point [1,m, 0] corresponding to the slope m = −A/B ofthe Euclidean line Ax + By + C = 0.
In particular, any two distinct parallel lines with slope m(m 6=∞) intersect at the line at infinity at the projective point[1,m, 0].
You an check that all vertical lines intersect at the projectivepoint [0, 1, 0].

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
The line Ax + By + Cz = 0 and the line at infinity intersect atthe point [1,m, 0] corresponding to the slope m = −A/B ofthe Euclidean line Ax + By + C = 0.
In particular, any two distinct parallel lines with slope m(m 6=∞) intersect at the line at infinity at the projective point[1,m, 0].
You an check that all vertical lines intersect at the projectivepoint [0, 1, 0].

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
The line Ax + By + Cz = 0 and the line at infinity intersect atthe point [1,m, 0] corresponding to the slope m = −A/B ofthe Euclidean line Ax + By + C = 0.
In particular, any two distinct parallel lines with slope m(m 6=∞) intersect at the line at infinity at the projective point[1,m, 0].
You an check that all vertical lines intersect at the projectivepoint [0, 1, 0].

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Projective Geometry - lines
[1,1,0]

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Back to Pappus’ Theorem
Let’s take another look at the configuration of points inPappus’ Theorem that didn’t work.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Back to Pappus’ Theorem
AB
C
A' B' C'

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Back to Pappus’ Theorem
AB
C
A' B' C'

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Back to Pappus’ Theorem
AB
C
A' B' C'

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Back to Pappus’ Theorem
AB
C
A' B' C'

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Back to Pappus’ Theorem
AB
C
A' B' C'

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Back to Pappus’ Theorem
AB
C
A' B' C'
[1,m,0]

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Proof of Pappus’ Theorem
Since we now know that parallel lines really do intersect, wecan proceed to prove Pappus’ Theorem under the assumptionthat all the lines intersect.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Proof of Pappus’ Theorem
Let Lij denote the line through points Pi and Pj , and let a, b, cdenote the points of intersection between the pairs of lines[L15, L24], [L16, L34], and [L35, L26] respectively. Pappus’Theorem asserts that the points a, b, c lie on a straight line.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Proof of Pappus’ Theorem
One proof proceeds by explicitly determining the coordinates ofthe points a, b, c , it is straightforward, but less trivial than onemight think.
Let Pi = (xi , yi ). We can assume thaty1, y2, y3 = 0 by rotating and sliding the picture so that P1,P2, and P3 lie on the x-axis and O lies at the origin. Then fori = 4, 5, 6, yi = kxi where k is the slope of the line OP6.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Proof of Pappus’ Theorem
One proof proceeds by explicitly determining the coordinates ofthe points a, b, c , it is straightforward, but less trivial than onemight think. Let Pi = (xi , yi ).
We can assume thaty1, y2, y3 = 0 by rotating and sliding the picture so that P1,P2, and P3 lie on the x-axis and O lies at the origin. Then fori = 4, 5, 6, yi = kxi where k is the slope of the line OP6.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Proof of Pappus’ Theorem
One proof proceeds by explicitly determining the coordinates ofthe points a, b, c , it is straightforward, but less trivial than onemight think. Let Pi = (xi , yi ). We can assume thaty1, y2, y3 = 0 by rotating and sliding the picture so that P1,P2, and P3 lie on the x-axis and O lies at the origin.
Then fori = 4, 5, 6, yi = kxi where k is the slope of the line OP6.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Proof of Pappus’ Theorem
One proof proceeds by explicitly determining the coordinates ofthe points a, b, c , it is straightforward, but less trivial than onemight think. Let Pi = (xi , yi ). We can assume thaty1, y2, y3 = 0 by rotating and sliding the picture so that P1,P2, and P3 lie on the x-axis and O lies at the origin. Then fori = 4, 5, 6, yi = kxi where k is the slope of the line OP6.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Proof of Pappus’ Theorem
You can now determine the coordinates of a, b and c explicitlyby writing down the equations for the lines L15, L24, L16, L34,L35 and L26.
You can then calculate the equation of the line through a and cand prove that b lies on that line.
There is a lot to keep track of!!
This is the most “straightforward” proof of Pappus’ Theorem.There are other theorems that make extensive use of the theoryof projective geometry.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Proof of Pappus’ Theorem
You can now determine the coordinates of a, b and c explicitlyby writing down the equations for the lines L15, L24, L16, L34,L35 and L26.
You can then calculate the equation of the line through a and cand prove that b lies on that line.
There is a lot to keep track of!!
This is the most “straightforward” proof of Pappus’ Theorem.There are other theorems that make extensive use of the theoryof projective geometry.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Proof of Pappus’ Theorem
You can now determine the coordinates of a, b and c explicitlyby writing down the equations for the lines L15, L24, L16, L34,L35 and L26.
You can then calculate the equation of the line through a and cand prove that b lies on that line.
There is a lot to keep track of!!
This is the most “straightforward” proof of Pappus’ Theorem.There are other theorems that make extensive use of the theoryof projective geometry.

ProjectiveGeometry and
Pappus’Theorem
KellyMcKinnie
History
Pappus’Theorem
Geometries
Picturing theprojectiveplane
Lines inprojectivegeometry
Back toPappus’Theorem
Proof ofPappus’Theorem
Proof of Pappus’ Theorem
You can now determine the coordinates of a, b and c explicitlyby writing down the equations for the lines L15, L24, L16, L34,L35 and L26.
You can then calculate the equation of the line through a and cand prove that b lies on that line.
There is a lot to keep track of!!
This is the most “straightforward” proof of Pappus’ Theorem.There are other theorems that make extensive use of the theoryof projective geometry.
![VIRTUAL RESOLUTIONS FOR A PRODUCT OF PROJECTIVE SPACESreiner/REU/REU2019notes/preprint-berkeschErman... · projective space because the New Intersection Theorem [Rob87] establishes](https://static.fdocuments.us/doc/165x107/5e7a09ca7334ee1c09229024/virtual-resolutions-for-a-product-of-projective-spaces-reinerreureu2019notespreprint-berkescherman.jpg)