Notes for C3103:

The Galaxy and the Interstellar Medium

Part I: Sections 1-4

Greg Bryan

October 17, 2007

Contents

1 Introduction 21.1 Galaxy Components and Equations . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

2 The Distribution of Stars and Gas in the Milky Way 42.1 Stars: a brief summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42.2 A brief history of our understanding of the Milky Way . . . . . . . . . . . . . . . . 62.3 The Components of the Milky Way . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

3 External Galaxies 73.1 Galaxy Luminosity Function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73.2 Galaxy Classification [Binney & Merrifield 4.3] . . . . . . . . . . . . . . . . . . . . 83.3 Elliptical galaxies . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93.4 Globular Clusters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113.5 The Black-hole galaxy relation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113.6 Disk Galaxies . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

4 Stellar Dynamics 144.1 The Gravitational Potential . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144.2 Dynamics (orbits) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 164.3 Virial Theorem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 184.4 An application of the Virial Theorem: The Tully-Fisher relation . . . . . . . . . . 204.5 The potential: bumpy or smooth? . . . . . . . . . . . . . . . . . . . . . . . . . . . 224.6 Measuring Galactic Rotation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 274.7 Spiral Structure . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 314.8 Galaxy Interactions I: Dynamical Friction . . . . . . . . . . . . . . . . . . . . . . . 344.9 Galaxy Interactions II: Tidal effects . . . . . . . . . . . . . . . . . . . . . . . . . . 384.10 Galaxy Interactions III: Mergers . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40

1

1 Introduction

On dark nights in places far from Manhattan, the Milky Way stretches across the sky like a faintlyglowing river of light. Seemingly completely different from the rest of the stars in the sky, it is infact composed of stars (as Galileo found by resolving individual Stars with a galaxy in 1609). Butnot only stars, the galaxy is also filled with gas and dust, which clump together into clouds andblock out the stars behind. It is these clouds of gas and dust which are responsible for the largedark patches that give the Milky Way its unusual visual texture (the stars are generally smoothlydistributed).

In this course, we will explore the physics of the galaxy, focusing on the distribution of starsand gas, with a particular emphases on explaining the often simple physical principles which areresponsible for the characteristics of the Milky Way. The focus will be on the physics, rather thanthe detailed astronomy. While we will spend most of our time talking about the Milky Way (as atypical spiral galaxy), other galaxy types will be discussed.

As little astronomical background will be assumed as possible, although inevitably, not all of theastronomical observations can be explained in a course of this nature. Most observations willbe presented without a detailed discussion of how they were obtained. In addition, astronomicaljargon will be kept to a minimum, and the focus will be on the physics of galaxies. A backgroundin general physics and calculus will be assumed.

The first part of these notes will be a whirlwind tour of the galaxy components and the set ofequations which guide its behavior. In this course, we will focus on the dynamics of the galaxy,and so use primarily the equations of stellar dynamics (Newton’s laws) for the stars, and the fluidequations for the gas. The microphysics of gas heating and cooling will be discussed briefly, andmany of the other important important ingredients (cosmic rays, magnetic fields) hardly at all.In a course like this, we have the choice between treating many subjects in a cursory fashion ordelving deeper on a smaller number of topics. We will err on the side of depth over breadth.

1.1 Galaxy Components and Equations

By mass (and most other measures), the three most important components of the galaxy are:

• Dark matter• Stars• Gas and dust

We will discuss these components in more detail later, but first let’s try to understand whatequations are appropriate to describe each of the components. While stars are, of course, composedof gas, they are generally very tightly bound and have a small radius compared to their separation.For example, the radius of the sun is about 7× 1010 cm, while the distance to the nearest star isabout 108 times larger than this. This means that physical collisions between stars are extremelyrare, and for the most part we can treat them as point particles following purely ballistic trajectories(i.e. the only force acting on them is gravity).

2

1.1.1 Collisionless Dynamics

This can be made more precise by estimating the mean length between collisions. A given star willcollide with another when the volume V swept out by its surface area over a time t becomes largeenough to include one other star, on average. Mathematically, this tells us that the product of thevolume and the number density of the other stars is one: V n = 1. The volume can be written asV = σl, where σ is the surface area of the star σ = πr2, and l is the distance the star must travelbefore it collides with another star. Solving this for l, we find that

l =1σn

. (1)

In kinetic theory, l is known as the mean free path. For typical conditions in the Milky Way, forwhich there is about 1 star per pc3, (1 parsec, or pc, is 3.09 × 1018 cm), we find l ∼ 1033 cm,or ∼ 1015 pc. This distance is much larger than the typical size of the galaxy (about 30 kpc, or3× 104 pc), confirming our previous expectation that collisions are unimportant for stars. We saythat stars are effectively collisionless.

While we do not know the properties of the dark matter, it is usually also assumed to be collision-less. This would certainly be true if the dark matter were composed of compact objects such asblack holes (which seems unlikely), or green peas (which seems even less likely), and also true if itwere some weakly interacting massive particle (WIMP), as is commonly thought.

If the only force acting on a collisionless particle is gravity, then the equations which describe itstrajectory are Newton’s equations:

v =dxdt

(2)

dvdt

= −∑

i

Gmim

|x− xi|3(x− xi) (3)

Where x and v are the positions and velocity of a particle of mass m. The force is computed bysumming the inverse square law postulated by Newton from all the other particles (excluding theparticle itself). We label these particles with an index i. These are the equations we will use formuch of the rest of the course. The solution for two particles can be computed exactly but for threeor more, no closed form solution is possible (although, of course, we can generate approximationsor solve the equations numerically).

1.1.2 Collisional dynamics

This situation is very different for the diffuse gas and dust in the Milky Way. We can see this bycalculating the mean free path again, this time for the typical properties of the interstellar medium(ISM). The density of atoms is n ∼ 1 per cm3, and atomic cross sections of a few times 10−17

cm2. The resulting mean free path is l ∼ 3 × 1016 cm, or ∼ 0.01 pc, which is much less than thetypical length scales of the ISM. Therefore, we can conclude that collisions are important. Thegas is collisional.

Strictly speaking we could still use Newton’s equations and add a force associated with the collisionprocess on to the right hand side of eq. 3, but in practice this is not the best way to solve theequations. Instead, we will take a statistical approach and treat the sea of particles as a gas with

3

some density ρ(x, t), mean velocity v(x, t) and temperature T (x, t). Note that these are fieldvariables, and describe the properties of the gas for every position in space x at every time t. Inthis view, we completely ignore the discrete nature of the gas (the fact that it is composed of lots ofsmall atoms), and everything is continuous. The equations which then describe how these variablesevolve are then partial differential equations, rather than the ordinary differential equations above.We will defer a more complete discussion of these equations until the second part of the course.

1.1.3 Course outline

Like the equations, this course will be divided between the collisionless component (mostly stars),which we will discuss in the first half, and the collisional component (mostly gas) which will be thefocus of the second half. However, in order to know what we need to explain with these equations,we will review the observations of, first, the Milky Way, and then external galaxies.

2 The Distribution of Stars and Gas in the Milky Way

In order to the describe the distribution of stars (and dark matter) in the Milky Way, it is usefulfirst of all to understand something about stars. The material below presents the briefest possibleintroduction to stars from the perspective of how they can be used to understand the galaxy – abetter source would be any (qualitative) introductory text on Stars, such as Carrol & Ostlie.

2.1 Stars: a brief summary

The essential observable that astronomers deal with is the flux of energy (photons) received fromdistance objects. We define the flux f to have units of energy per unit area per unit time (in cgserg cm−2 s−1). More generally, we can use spectroscopes to separate photons of different energy,or wavelength λ. From this we want to know, at least, the distance d, luminosity L, mass M ,velocity v, as well as age and composition (at the very least – there are, of course, many otheruseful quantities). Generally the most problematic of these is the distance.

The most direct way to measure the distance is trigonometric parallax. This refers to theapparent motion of a nearby star against the background of more distance objects as the earthrotates around the sun. This technique is crucially important and gives rise to our definition of theparsec: 1 pc is the distance of a star if it shifts its position by 1 arcsec (there are 3600 arcsecs in adegree) as the earth moves by 1 AU (the distance between the earth and the sun). Unfortunatelythis technique is currently limited to stars within about 100 pc.

One of the most common techniques to go beyond this limit is the idea of spectroscopic parallax.This uses the idea that the spectrum of a star tells you much about the star itself. In particular,the surface temperature derived from analyzing the spectrum tells you much about a star’s mass,with more massive stars generally having higher temperatures (at least for stars on the so-calledmain sequence, during their regular hydrogen burning lifespan). An analysis of the spectral linesgenerated by various elements on the star’s surface tells you even more. By matching a spectrumfrom an unknown star to a star with a known type, we can identify the star’s intrinsic luminosity,mass, composition and age (assuming we know all these things either directly from theoreticalconsiderations, or more often from the detailed analysis of a nearby star of that type). The

4

distance d can then be determined based on the measured flux via f = L/4πd2. In practice wemust also take into account the dimming effect of dust between us and the star.

The star’s velocity can be measured from the Doppler shift of one of its spectral lines. Thesespectral lines come from the transition between two quantum states of an atom. Since the intrinsicwavelength of this transition is generally well-known, the measured shift in wavelength can be usedto determine the star’s velocity toward or away from us (the velocity in the plane of the sky canonly be measured via the star’s proper motion — that is, the observed movement of the star onthe sky after many years of motion).

Finally, the strength and number of the spectral lines also tells us about the chemical compositionof the star. Since the universe began with nearly all of its gas in the form of either hydrogen, orhelium, all other elements are quite rare and astronomers refer to them as ”metals”. Since theseheavy elements, or ”metals” are formed only in the cores of large stars and in supernova explosions,the amount of metals increases with time, and the metallicity of a star is an indication of howmany generations of stars have come before (the more supernovae, the higher the rate of metalpollution). The metallicity Z of a star is defined as the ratio of the mass in elements heavierthan helium to the total mass of the star. This is sometimes given compared to the solar value,which is approximately Z ≈ 0.02.

2.1.1 Stellar statistics

The mass of stars ranges from 0.08 M, the smallest mass for which hydrogen will fuse in the coreof the star, up to several hundred solar masses (here, as in the rest of these notes, we will use thesymbols M, L and R to denote the mass, luminosity and radius of the sun). The luminosityL of a star increases quickly with mass; a rough guideline is that the stellar luminosity scalesapproximately with mass as L ∝ M4. Note that this is not steep enough for low mass stars, andis too steep for high mass stars, above about 10 M (for which L ∝ M2.2). Stars more massivethan about 8 M will end their lives as a type II supernova.

More massive stars are, of course, rarer. We can define the initial mass function (IMF) as the rateof star production as a function of mass. For stars with masses equal to and great than the sun’s,the IMF falls off quickly with mass: dN/dM ∝M−2.35 (this is known as the Salpeter IMF, for theastronomer who suggested it). Below a solar mass, the number is approximately constant (or itmay even fall slightly). The total number of stars born with all masses can be found by integratingthis function over mass:

N =∫ ∞

0

dN

dMdM (4)

Putting the Salpeter IMF into this tells us that most stars are born with low masses (a typicalstar has a mass not much lower than the sun’s). The total mass of stars born can be computedwith the mass-weighted integral:

M =∫ ∞

0MdN

dMdM (5)

The mass-weighting tells us that the stars which contribute most of the mass are a little larger,but still most of the mass of stars is not too much above one solar mass (i.e. the most massivestars are still too rare to contribute much of the mass in stars in the galaxy).

However, things change when we talk about which stars contribute most of the luminosity. Thiscan be computed in the same way as the above integral, but this time weighting with L. Since

5

L ∝ Mα, where α = 2.2 for the most massive stars, the integral is now dominated by the upperend of the luminosity function. In fact, formally the total luminosity diverges if we integrate outto infinite mass, but fortunately something saves us from the potentially painful consequences ofan infinitely bright universe. We are saved by the fact that massive stars live for only a shortperiod of time so at any particular moment in time, there are even fewer high mass stars aroundthan the initial mass function tells us. Remember that the initial mass function tells us how manystars are born with a given mass; we might define the current mass function as the distribution ofstars which are currently around – this function would drop even more steeply with mass than theIMF.

2.2 A brief history of our understanding of the Milky Way

This interesting topic is adequately covered by most introductory undergraduate astronomy texts,and so we will not discuss it further.

2.3 The Components of the Milky Way

We discuss six distinct components of the milky way: the stellar disk, the gas disk, the (stellar)bulge, the stellar halo, the globular clusters, and the dark matter.

Most of the stars in the galaxy are distributed in a thin disk which rotates around the center ofthe galaxy in circular orbits. We use a set of cylindrical coordinates to describe the distribution ofstars, where R is the radial coordinate, z is the height above or below the plane of the disk, andθ (which varies from 0 to 2π) is the angle from some radial vector in the plane of the disk. Thedistribution of stars is given by:

N(R) = N0 exp (−R/Rd) exp (−z/zd) (6)

where Rd ≈ 3.5 kpc is known as the radial scale length and tells how the number of stars fallsoff with distance from the center of the disk. The thickness of the thin disk (zd) is about 300 pc.The stars in the disk range from very young to moderately old and are generally highly enrichedin heavy elements (metals).

In the last two decades, it has been recognized that there is another disk, a thick disk which hasa similar radial scale-length but has zd ≈ 1400 pc, nearly 5 times thicker than the thin disk. Thisthick disk has a mass which is about 50 times lower than the thin disk, and contains stars whichhave higher non-circular velocities, as well as different ages (and compositions). The origin of thethick disk is still debated, but is generally thought to have originated in a merger event early inthe Milky Way’s history.

The bulge is a central, roughly spherical conglomeration of stars. The bulge is only a few kpc insize but contains almost 1/3 as much mass as the think disk, so it is a major component of thegalaxy. The spatial distribution of bulge stars is complicated by the fact that the Milky Way isthought to host a bar in the center (see the next section on galaxy morphology), and so we donot provide a formula here. The stars in the bulge are a mixture of many types (various ages andchemical abundances).

The stellar halo is a diffuse collection of stars which have non-circular orbits carrying them outto large radii. Near the sun, they show up as ”high-velocity” stars because they do not share the

6

same circular velocity as the rest of the disk stars. Halo stars are uniformly very old and very metalpoor (often only a few percent of the heavy elements in the sun). The density of halo stars nearthe sun is very low, but they are spherically symmetric around the center of the galaxy (ratherthan disk-shaped). The precise density profile of the halo is not well-known, but falls off rapidlywith density (ρ(r) ∝ r−3).

Finally, the Milky Way has about 300 globular clusters (GCs). These are very compact starclusters with masses of around 106M, and radii of only a few pc. They orbit the Milky Way ina mixture of orbits, with the oldest ones following a similar distribution as the halo stars, and theyounger ones arranged in more of a disk.

The total amount of dark matter is thought to be about 1012M, at least 10 times larger than allthe other components. The precise nature of the dark matter is unknown, although it is generallythought to be composed of some sort of so-far undetected elementary particle that interacts withregular matter so weakly that it is effectively invisible (a bit like the neutrino). Another, lesspopular, explanation is that the Newtonian laws of gravity are incorrect when confronted with theunusual conditions of the galaxy. We’ll almost always assume that the dark matter is composed ofa collection of particles which obey Newton’s laws, in which case what is important is not the massof each individual particle, but the mass density of dark matter in the galaxy (something whichcan be measured through its gravitational impact). The precise distribution of the dark matter isnot well-known, but it seems to be much more spread out than the stars.

2.3.1 Stellar Populations

As we have noted in the discussion of each component, the stars found in the disk and the haloare systematically different from one another. The disk stars tend to be young and metal rich,while the halo are old and metal poor. This led to the division of stars into two populations, withPopulation I stars inhabiting the disk, and Population II in the halo. The bulge contains amix of both populations. The thick disk is intermediate, with mostly older stars, but many metalrich ones as well.

3 External Galaxies

One of the most obvious facts about galaxies is that they come in a variety of sizes and luminosities.Perhaps more surprisingly is that, for a given size and luminosity, there are usually a number ofdifferent types. Remarkably, the inherent reason for this variety is still not well understood. It isone of the key requirements for a successful theory: that we can reproduce the rich diversity ofgalaxies.

In this section, we review the classification of galaxies, first of all focusing on the galaxy luminosity,and then discussing classification based a galaxy’s appearance, or morphology.

3.1 Galaxy Luminosity Function

We define Φ(L)dL as the number density of galaxies with luminosities from L to L + dL. Theluminosity (energy per unit time) L could be in a particular wave-band or it could be integrated

7

over all wavelengths (the bolometric luminosity). In either case, the luminosity function is usuallynormalized so that, ∫ ∞

0Φ(L)dL = ngal (7)

where ngal is the local density of all galaxies (we have not specified it but the luminosity functioncan and does vary with position). The luminosity function is a difficult thing to measure but itis clear that it drops quickly at large luminosity and has a large extension to low luminosities. Auseful parameterization is the known commonly as the Schechter function:

Φ(L) = (Φ∗/L∗)(L/L∗)α exp(−L/L∗), (8)

which is simply a power-law of slope α with an exponential cutoff. The cutoff occurs at L∗ andas long as α > −2 (which is observationally always the case), the total light integrated over allluminosities is finite:

Ltotal =∫ ∞

0LΦ(L)dL = Φ∗L∗Γ(2 + α)

For the typical value of α = −1, the Gamma function is unity and since Phi∗ is approximately thenumber density of galaxies with luminosity of L∗, the total light is clearly contributed mostly bygalaxies around L∗. Our own Milky-Way galaxy has approximately this luminosity, and it definesthe typical brightness of a large galaxy.

On the other hand, the total number of galaxies is not always convergent and indeed large numbersof low-luminosity galaxies are observed (although there does appear to also be a lower cutoff whichis not modelled by the Schechter function). The luminosity function is difficult to determineobservationally for a number of reasons. First, the low luminosity end is difficult to determinebecause faint galaxies can only be seen nearby. More worringly, the surface brightness of manygalaxies falls close to the limit which can easily be observed. Even intrinsically luminosity galaxiescan appear dim if they are large and spread across a large region of the sky. Indeed, recent workhas uncovered a whole population of low-surface brightness (LSB) galaxies. These LSB galaxiesare typically only a few percent of the surface brightness of the background sky and so are difficultto see. However, they are clearly of great importance both because they may be as numerousas their high-surface brightness cousins, but also because many appear to be largely dark-matterdominated and so provide good cases to study the distribution of non-luminous matter in galaxies.

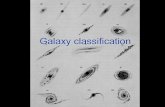
3.2 Galaxy Classification [Binney & Merrifield 4.3]

There are many ways of classifying galaxies but by far the most well-known is the Hubble system,which has originally suggested by Hubble in his 1936 book, The Realm of the Nebulae. Galaxy clas-sification is a topic all of its own (for example see Sidney van den Bergh’s Galaxy Morphology andClassification), so here we just remind readers of the basic classes and the difficulties encounteredin classification by any system.

In Hubble’s tuning-fork diagram, on the left are the sequence of elliptical galaxies spanning therange from circular to highly elliptical systems. These are denoted En, where n = 10(1 − b/a) iscomputed by measuring the axial ratio b/a of the ellipse formed on the sky. Note that these aremeasured from the projection on the sky, so that the intrinsic three-dimensional distribution maybe considerably different (in fact, in general elliptical galaxies are likely to be triaxial, and the axescan change as a function of radius).

8

The elliptical systems are often further sub-divided into dwarf types (dE), although it is not clear ifthe dwarfs are simply small elliptical or a class of their own. Dwarf spheroidals (dSph) are a closelyrelated type, the primary difference being that they are even less luminous and more diffuse (theyare an interesting targets for dynamical studies because of their very high dark matter content).With the advent of new technology that permits detailed studies, the smallest galaxies have becomea topical area of research. For a summary of known dwarf galaxies in the local group, see the articleby Mateo et al. in the 1998 Annual Reviews of Astronomy and Astrophysics (Vol 36, p. 435).

After the ellipticals, Hubble’s diagram splits in two, with two parallel sequences differentiated bythe presence (top sequence) or absence (bottom) of a stellar bar in the center. The first galaxiesare the so-called lenticular or spheroidal galaxies, designed S0 (or SB0 if there is a bar). Thesesystems appear to be strongly oblate like a spiral system but without any clear spiral structure.Like ellipticals, they usually have little dust or gas content, although some systems can containsignificant amounts of dust: the strength of the dust is sometimes signified by a subscript rangingfrom S01 (no dust) to S03 (prominent dust lane).

After the spheroidals come the spirals, designated Sa, Sb or Sc depending on three characteristics:the tightness of the spiral arms, the size of the central bulge and the definitions of the arms. Spiralswith tight, well-defined arms and a strong central bulge are Sa, while Sc systems have loose,poorly defined spiral arms and little or no central spheroidal component. Note that these threecharacteristics almost vary together, but exceptions exist which can make classification difficult.If the spiral has a bar, it is classified with SBa, SBb or SBc. Additions have been suggested tothis system, including de Vaucouleurs addition of Sd and Sm spiral systems that include galaxieswhich are looser or have even more poorly defined arms than the Sc class.

Hubble thought that galaxies evolved along his sequence, going from elliptical (“early”) galaxiesto spiral (“late”) galaxies. While this idea is no longer thought likely, the terminology has stuck.It is not uncommon to find a numerical T stage assigned to the Hubble type for the use in someforms of statistical analysis. This ranges from -5 (E0) to 0 (S0) to 6 (Sc) to 10 (Irr). Entirelyoutside of this sequence are the irregular galaxies Irr which lack symmetry or well-defined spiralarms, and the peculiar galaxies which may be undergoing a merger or interaction.

As we will see in more detail later, galaxies are not uniformly distributed in space. While isolated,field galaxies do exist, the majority of galaxies are found in groups or clusters. Very small groups,like the local group, consist of only a few large galactic systems. Large groups may have up to 100,while full-fledged clusters often have thousands of large galaxies. Galaxies of different types are notequally represented in different environments. In particular, ellipticals are much more likely to befound in dense cluster cores than in the field, while spirals show the opposite trend. This is mostcommonly called the morphology-density relation and is clearly telling us something about whatsets galaxies morphology, but it is not clear whether spiral galaxies are transformed into ellipticalsby the dense environments of clusters, or if such regions preferentially formed elliptical galaxies evenbefore the cluster formed (clusters are thought, from both theoretical and observational evidence,to be younger than galaxies).

3.3 Elliptical galaxies

We first address elliptical galaxies in more detail. Elliptical galaxies are in some ways simplierbecause they generally do not have gas and dust, so are largely stellar systems. On the otherhand, they do not have the simple orbits that characterize disk systems. We start with radial

9

structure of elliptical galaxies, and then move on to global properties of the systems and theirscaling relations.

3.3.1 Radial brightness profile [Binney & Merrifield 4.3]

While elliptical galaxies are generally not spherical, it is often useful to examine how their bright-ness varies as a function of distance from the center. This is done either by fitting an ellipticalmodel or by fitting the major and minor axes separately. In either case, it is found that the surfacebrightness (i.e. energy per unit second per unit area per unit solid angle) measured in magnitudeper square arcsec (µ) varies with projected distance R as R1/4. If we write surface brightness inlinear units (recall that I ∝ 10−0.4µ), then it is usually to express this relationship as:

I(R) = Ie exp(−7.67[(R/Re)1/4 − 1]). (9)

The numerical factors are chosen such that if 1/2 of the total light (for a spherical system) isemitted within Re: ∫ Re

0πRI(R)dR = Le/2.

For this reason, Re is a useful measure of a galaxies size and is called the effective radius. It is alsouseful to define the mean surface brightness within the effective radius: Le = πR2

e < I >e.

While most elliptical galaxies follow this distribution, some giant elliptical galaxies show an excessof stars at large radii. These cD ellipticals are generally found at the center of large groups orclusters of galaxies. The excess is commonly interpreted as an overall envelope of stars that moreproperly belong to the clusters as a whole than to the cD galaxy. This intra-cluster light cancontribute significantly (20% in some cases) of the observed starlight from the entire cluster.

3.3.2 The relation between luminosity and velocity

Elliptical galaxies are unlikely to be significantly supported by bulk rotation, as is the case for spiralgalaxies. However, the stellar velocities still give an indication of the gravitational mass. Usually,it is impossible to measure individual stellar velocities in elliptical galaxies, but the distributionof line-of-sight velocities can still be measured as a function of position across the galaxy. This isdone by measuring the spread of stellar emission line caused by the Doppler shifting of all of thestars at that (projected) distance. The velocity dispersion at the center of an elliptical galaxy isdenoted by σ0 and is usually straightforward to measure. It was noticed quickly that this quantitywas strongly correlated with the galaxies luminosity:

Le ∼ σ40 (10)

This is known as the Faber-Jackson relation. Other relations between these quantities and < I >e

or Re were found, but all of them (including the Faber-Jackson relation) can be thought of asprojections of a single correlation between three quantities. This relation defines a two-dimensionalplane within the three-dimensional space define by (say), Re, < I >e and σ0.

One common parameterization of this is given by:

logRe = 0.36µe + 1.4 log σ0, (11)

where µe is the surface brightness in units of blue magnitudes per arcsec (recall < I >e∝ 10−0.4µ),Re in units of kpc and σ0 in km/s.

10

3.4 Globular Clusters

Although Globular clusters are generally not viewed as galaxies in their own right, they do over-lap in luminosity with dSph galaxies. However, they are many times more centrally concentrated(their effective radii are typically a few pc) and so appear to be a different type of beast. Thedistribution of GC luminosities appears to be Gaussian, with a central value of a few times 105

solar luminosities. Both spiral and elliptical galaxies contain globular clusters (the Milky Way hasapproximately 160) and we can compute the specific frequency of globular clusters as the ratio oftheir number to the luminosity of the galaxy: SN ∝ NGC/Lgal. More precisely the definition isgiven in terms of the galaxies V magnitude MV :

SN = Nt10−0.4(MV +15). (12)

There appears to be a trend with SN decreasing from left-to-right in the Hubble diagram. It isnot obvious why bulges and ellipticals should have relatively more globular clusters for their givenluminosity. In fact, the origin of globular clusters in general is not understood. The Milky Wayis observed to have a bi-model distribution of GC’s, with roughly half been old and metal-poor,with the rest being younger and more metal rich.

3.5 The Black-hole galaxy relation

Recently, it has become clear that all local galaxies with significant spheroidal components hostsupermassive blackholes in their centers. Even more remarkably, there is a fairly tight relationbetween the mass of the black-hole and the mass of the bulge. This (“Magorrian”) relation indicatesthat roughly 0.5% of the mass of the bulge is in the supermassive blackhole. It is sometimes writtendifferently, in terms of the black-hole massMBH and the velocity dispersion of the bulge or spheroid:

MBH ∝ σ4.5. (13)

It is clear that these blackholes where quasars at some point in the past. In fact, assuming thatthese black holes grow from the inspiral of gas in an accretion disk accompanyed by the emissionof roughly 10% of the gravitational energy of the infalling mass (as General Relativity predicts),then the resulting radiative energy agrees well with the total energy that quasars are observed toproduce. This comparison is known as the Soltan argument.

The fact that the mass of black holes is tightly correlated to the bulge mass tells us that black-holesare closely connected to their large halos. While it is not clear which way causality runs in thiscase (i.e. do galaxies control how much gas is fed onto black holes or do quasar outflows regulatestar formation in spheroids), it is not hard to imagine that the vast amounts of energy involved inquasars must have a substantial impact on the galaxies that host them.

3.6 Disk Galaxies

3.6.1 Radial Brightness profiles [Binney & Merrifield 4.4]

While ellipticals follow the de Vaucouleurs R1/4 profile, spiral galaxies have an exponential fall-off to their surface brightness profile. In order to measure this, it is necessary to measure theinclination angle of the disk (the angle between the observer and the normal of the disk) and

11

correct for the effect of this inclination. Once this is done, we find I(R) = I0 exp(−R/Rd), whereRd is the disk scale-height and typically takes values of a few kpc. In fact, this is a significantoversimplification because the vast majority of observed disks show a central excess which can befitted by a spheroidal profile. This central spheroidal or bulge can be seen as a spherical additionin the centers of most spiral galaxies (including in the Milky Way). The relative importance ofthe disk and the bulge can be measured by decomposing the profile into the two components andcomputing the ratio of the total light in each component. This is known as the disk-to-bulge ratio(B/D) and is correlated with the spiral type (Sa’s having a smaller value than Sb’s).

3.6.2 The relation between circular velocity and luminosity

The Tully-Fisher relation is a correlation between the galaxy’s luminosity and the maximum ro-tational velocity of the gas, often measured via the HI 21 cm line width:

L ∝ V αmax (14)

where α ∼ 4 (although the value appears to depend on the wavelength at which the luminosity ismeasured).

3.6.3 The Interstellar Medium

Besides stars, spirals galaxies like the Milky Way contain gas, which can be observed in a numberof ways. One of the primary ways is via observations of the 21 cm emission from the hyperfinetransition of neutral hydrogen (HI). Such observations of the external galaxies show that the HIdisks often extend considerably further than the stellar disk. The lack of star formation at largeradii is probably due to the fact that the disk at that point has a density below the critical densityfor gravitational instabilities to form.

The HI disk is also often observed to deviate from cylindrical symmetry. For example, spiral disksare often observed to be lopsided and have warps (the stellar disk can also warp). Some galaxiesexhibit holes in the HI disk, due in part to ionization from recently formed massive stars or tosupernovae explosions. In both cases, it usually requires a cluster of recent star formation to makea noticeable hole.

HI observations often show a large hole in the center of the disk. Radio and sub-mm observationsof molecular emission lines, in particular CO, often show emission from these regions, indicatingthat much of the gas is dense and cold enough to be molecular.

Infrared emission is associated with dust, which is mostly a good black-body although there areinteresting spectral signatures at various wavelengths. Dust is a strong absorber of UV radiationand in starbursting galaxies most of the radiation is reprocessed by dust into the infrared.

3.6.4 Dark Matter

One of the most important applications of HI observations is to measure the rotation curve of agalaxy and so determine the density distribution of gravitating mass. It is this observation whichfirst pointed to the need for dark matter in disk galaxies.

12

The gas (or stellar) redshift can be converted to a circular rotation speed which, assumes sphericalsymmetry, gives the enclosed mass via v2

c = GM(r)/r. Such observations gave some of the firstand strongest indications of the existence of dark matter. Unfortunately, for typical disks suchas the Milky Way, the local disk is dominated by stars and gas rather than dark matter (whichis more important at larger radii). Therefore, a correction for the stellar component is necessarywhich requires assuming a mass-to-light ratio for the stars. This can be circumvented by makeobservations of so-called Low Surface Brightness (LSB) disks which have a particularly low gasdensity and so are dominated by dark matter over most or all of the disk. These observations areusually fit to one of two dark matter profiles:

ρISO(r) =ρ0

1 + (r/a)2ρNFW(r) =

ρ0a3

r(a+ r)2(15)

The first is similar to the profile for an isothermal sphere and has a constant density within thecore radius a, while falling as r−2 at large radii. The second profile comes from N-body simulationsof Cold Dark Matter halos and exhibits a cusp at small radius, while falling steeply as r−3 forr >> a. It appears that a substantial fraction of observed LSB galaxies are not good fits to theNFW profile, but it is still not clear if this is a true contradiction between CDM N-body simulationand observations or if one or other will change as the observations and models (which currentlydo not include stars and gas in a self-consistent way) improve.

13

4 Stellar Dynamics

Stellar dynamics is the study of self-gravitating systems composed of stars. As we remarked inthe introduction, stellar collisions are very rare and so we can effectively treat a system of stars asa system of point particles. In this section, we will develop the main tools of stellar dynamics andsee what they tell us about the current state and future evolution of galaxies, and the stars withinthem.

4.1 The Gravitational Potential

We begin with gravity. From Newton’s laws, the acceleration on a particle is given as the sum ofthe inverse-square law forces from all the other partices:

dvdt

= −∑

i

Gmi

|x− xi|3(x− xi)

= −∫

V

Gρ(x′)|x− x′|3

(x− x′)d3x′ (16)

In the second line, we have transformed the sum into an integral by assuming that we can writedown a smooth density distribution ρ(x). The integral is over all space. We can write this in aeasier form if we note the following identity:

∇x

(1

|x− x′|

)= − x− x′

|x− x′|3, if x 6= x′ (17)

which can be straightforwardly demonstrated by writing it out in cartesian coordinates. Note thatwe use the notation ∇x to indicate that the differentiation is done with respect to x (as opposedto x′). This lets us re-write the right-hand side of equation (16) as

dvdt

= ∇x

∫V

Gρ(x′)|x− x′|

d3x′ = −∇xΦ(x). (18)

We have been able to take the gradient operator out if the integration because the integration isover x′, while the gradient is with respect to x. This shows that the force can be written entirelyas the gradient of some quantity (the potential Φ(x)) instead of a force itself. This is true becauseof the nature of the gravitational force and its purely radial nature. Since a field is much easier tothink about and work on than a full vector field, we will mostly use the potential, which we writedown here for completeness sake:

Φ(x) = −∫

V

Gρ(x′)|x− x′|

d3x′. (19)

This is an important simplification, but we can write the potential in an even simpler way, thatdoesn’t involve and integral at all. This requires some slightly contorted reasoning to prove (wefollow Binney & Tremaine’s derivation). The first step is to apply ∇2

x to both sides of equation(19) to get:

∇2xΦ(x) = −

∫V∇2

x

Gρ(x′)|x− x′|

d3x′

14

= −∫

V∇x ·

Gρ(x′)|x− x′|3

(x− x′)d3x′ (20)

= −∫

VGρ(x′)

[3

|x− x′|3− 3(x− x′) · (x− x′)

|x− x′|2|x− x|3]d3x′

= 0 if x 6= x

where we have used the identify in equation (17). This result tells us that any contribution to thepotential must come from a very small region around x = x′. If we restrict the volume integral toa small sphere with radius h around this point, where h can be made arbitrarily small. Since h isvery small, the density can be assumed to be constant across this very small region and it can betaken out of the integral. From equation (20), we get:

∇2x = −Gρ(x)

∫|x′−x|≤h

∇x ·[

x− x′

|x− x′|3]d3x′

= Gρ(x)∫|x′−x|≤h

∇x′ ·[

x− x′

|x− x′|3]d3x′

= Gρ(x)∫|x′−x|=h

x− x′

|x− x′|3· d2S

The second step is permitted because x is arbitrarily close to x′, and in the third step we havemade use of the divergence theorem, which tells us that the volume integral of ∇· f can be writtenas a surface integral of f ·d2S. The integral is over the sphere with radius h, and d2S is the surfaceelement on the sphere and points in a direction normal to the surface. The vector x − x′ is alsonormal to the surface and has a length h (since it lies on the surface of the sphere). This makesthis integral easy to evaluate and we get simply 4π. The final result then in Poisson’s equation forthe potential:

∇2Φ(x) = 4πGρ(x). (21)

This result is particularly useful when we start looking at spherically symmetric systems for whichthe density profile depends only on radius r. It is useful to invoke two of Newton’s theorems aboutspherically symmetric systems which we will state without proof (see Binney and Tremaine for aproof).

Newton I: Inside a spherical shell of uniform density, the net acceleration from that shell is zero.This also means that the potential is constant inside a shell.

Newton II: The acceleration outside a spherically symmetric shell of mass is the same as if allthe mass is at the center.

That is, we can treat a spherically symmetric object as if all of the mass inside a radius r is at thecenter – this simplifies calculations enormously, and is implicit in our usual method for determiningthe enclosed mass within M(< r) in a galaxy with:

v2c (r) =

GM(< r)r

(22)

We can now write down a general expression for the potential of any symmetric distribution withdensity ρ(r), by dividing the calculation into shells with r′ < r and shells with r′ > r:

Φ(r) = −[GM(< r)

r+∫ ∞

04πGρ(r′)r′dr′

](23)

where by M(< r) we mean the integrated mass within radius r.

15

4.2 Dynamics (orbits)

The orbit of a given star can, in principle, be calculated once the density distribution is specified,by computing the potential and then integrating the equations of motion:

d2xdt2

= ∇Φ(x) (24)

Energy conservation for time-independent potentials

We can quickly derive one useful result if the potential does not depend on time. We start bydefining an energy for a given particle as E = mv2/2 + mΦ(x). To find how this varies wedifferential with respect to time:

d

dt

[mv2/2 +mΦ(x)

]= mv · dv

dt+m

dΦdt

(25)

The dΦ/dt term can be evaluated if the potential does not depend on time with the chain rule:

dΦdt

=dx

dt

dΦdx

+dy

dt

dΦdy

+dz

dt

dΦdz

= v · ∇Φ = −v · dvdt

(26)

The last step follows from Newton’s law. Substituting this into the previous equation for thederivative of the energy we find that dE/dt = 0. This tells us that the energy (kinetic pluspotential) of a star is constant along its orbit providing that the potential itself is time-independent.

We can use this to find the escape velocity for a particle at a given particle. By escape velocity,we mean that given this velocity, the particle will be able to go to arbitrarily large distances fromthe center, at which point the potential is 0. The total energy is also zero (or larger) at this point,telling us that a star is bound if its total energy is less than zero. At a radius r, if E = 0, then thekinetic energy is the negative of the potential energy so:

v2escape ≥ −2Φ(x) (27)

Energy conservation for time-dependent potentials

If the potential does change with time, then the energy of a given particle can vary. However, wecan still derive a weaker result for the total energy of the entire system. Intuitively we know thismust be constant, but it is good to prove it anyway. We start with taking the derivative of thekinetic energy:

d(KE)dt

=d

dt

(12

∑i

mivi · vi

)=∑

i

mivi ·dvdt

= −∑

i

mivi ·∑j

Gmj

|xi − xj |3(xi − xj) (28)

The second line uses the definition of the acceleration of particle i as arising from the summedforce from the other particles (note that we must exclude the term i = j from this sum because a

16

particle does not exert force on itself). We have computed this starting with particle i but we arefree to do it for particle j as well, to get:

d(KE)dt

= −∑j

mjvj ·∑

i

Gmi

|xj − xi|3(xj − xi) (29)

If we sum these two expressions then we get:

2d(KE)dt

= −∑

i

∑j

Gmimj

|xi − xj |3(xj − xi) · (vi − vj)

= −∑

i

∑j

Gmimjd

dt

(1

|xi − xj |

)

= − d

dt

∑i

∑j

Gmimj

|xi − xj |

= −2

d(PE)dt

(30)

In the last step we have defined the potential energy PE, so that the sum of the kinetic andpotential energies are constant with respect to time. If the distribution of matter is continuousand we have a density ρ(r) instead of a set of galaxy positions, the PE is

PE =12

∫Vρ(x)Φ(x)dV.

Conservation of momentum

Specializing to the motion of a star moving in a central force, we can quickly establish the conser-vation of momentum: L = mx× v. We can take the time-derivative of this:

dLdt

=dxdt×mv + x×m

dvdt

= 0 (31)

The first time is zero because dx/dt = v and the cross-product of a vector by itself is always zero.The second term is zero in a central force because dv/dt ∝ x.

Motion in a central potential

We examine one last special orbital case – that of an object moving in a centrally-directed gravi-tational force (e.g. the planets moving around the sun). This case has exact solutions. We startby noting that if the motion will stay confined in the plane specified by the velocity vector and theinitial acceleration vector. This simplifies things so we need only consider planer motion. We use aradius-angle coordinate system defined by the radial unit vector r and the (locally perpendicular)angular vector θ. These can be defined in terms of the x-y cartesian coordinates by:

r = x cos θ + y sin θθ = −x sin θ + y cos θ

17

We will need the following results which can be readily derived:

dr

dθ= −x sin θ + y cos θ = θ

dθ

dθ= −x cos θ − y sin θ = −r

Now we are ready to derive the equations of motion in this coordiant system. We begin with theacceleration for x = rr:

d2xdt2

=d

dt

[d

dt(rr)

]=

d

dt

[dr

drr + r

dθ

dtθ

](32)

To continue we note that we can use the chain rule to rewrite d/dt as

d

dt=dr

dt

d

dr+dθ

dt

d

dθ

After some work we can write the d2x/dt as

d2xdt2

= r

[d2r

dt− r

(dθ

dt

)2]

+ θ

[rd2θ

dt2+ 2

dr

dt

dθ

dt

]= ag r (33)

The angular part is equal to zero (for a centrally-directed force) and is just a restatement ofthe conservation of angular momentum (i.e. L = r2dθ/dt is constant). The radial part is moreinteresting because it is equal to the radial acceleration ag. For a circular orbit, d2r/dt2 = 0, andso we have

r

(dθ

dt

)2

=v2c

r= ag =

GM

r2(34)

This result is, of course, very useful and is used to define what we mean by the circular velocityvc = rdθ/dt.

In fact, we can write down solutions very the general case of non-circular motion but we will notneed such solutions here. Interested readers are referred to Binney & Tremaine (section 3.1) aremost books on dynamics.

There is more to say about orbits, in particular nearly circular orbits, but we will defer this to alater section.

4.3 Virial Theorem

The conservation of energy is a useful tool, but we can derive even better tools for systems whichare in equilibrium. We have to be clear about this idea of equilibrium for a gravitating systembecause individual stars are, of course, still in motion. But this is no different than equilibriumfor a gas, in that individual atoms can still be in motion for a parcel of gas which is not changingits gross properties (temperature, density, etc.).

There is a major difference between a gas, and a self-gravitating system, and this has to do withthe fact that gravity is a long-range force. Of course the electrostatic force is also long-range,but on average most gases are electrically neutral and so the net electrostatic force is small. Thishas to do with the fact that mass only has one sign (even anti-matter has a positive mass), whilecharge can be both negative and positive.

18

Because of this long-range force, self-gravitating systems must be considered as a whole – wecannot divide the system in two and analyze each half separately. We can think about thisqualitatively first, and then derive a quantitative results. Imagine two different star clusters –both self gravitating, and both with the same total mass M but the first is spread out and diffuse,while the second is concentrated. In the diffuse cluster, the mean density ρ is low, and thecharacteristic size R is large. What about the velocities? Well, typical accelerations will be aroundGM/R2 (from Newon’s law), and so velocities will be this multiplied by how long it takes to travelacross the cluster (acceleration multiplied by time), which is about R/v. So we get v ∼ GM/vR,or solving for v, we get v ∼

√GM/R. This means that for the two clusters with the same mass,

the larger one (larger R) will have smaller velocities than the more concentrated one.

We can quantify this more precisely with the virial theorem, which we now derive. We followa similar path as for the energy conservation. We begin with Newton’s law for the motion ofparticle i:

midvi

dt=∑j

Gmimj

|xi − xj |3(xi − xj) (35)

and multiply this by xi:

midvi

dt· xi =

12mi

d2

dt2(xi · xi)−mivi · vj =

∑j

Gmimj

|xi − xj |3(xi − xj) · xi

(the second step may take some thinking about). If we then sum this over all particles i, we find:

12d2

dt2

∑i

mi(xi · xi)−∑

i

mivi · vi =∑j

∑i

Gmimj

|xi − xj |3(xi − xj) · xi

It is common to define∑

imi(xi ·xi) as the moment of inertia and denote it as I. The second termin the equation above we be readily recognized as the kinetic energy KE, so we can re-write it as:

12d2I

dt2− 2KE =

∑j

∑i

Gmimj

|xi − xj |3(xi − xj) · xi

As we did for the previous derivation, we can repeat this reversing the role of i and j to get:

12d2I

dt2− 2KE =

∑j

∑i

Gmimj

|xi − xj |3(xi − xj) · xj

We can add these and divide by two to get:

12d2I

dt2− 2KE =

12

∑i

∑j

Gmimj

|xi − xj |3(xi − xj) · (xi − xj) =

12

∑i

∑j

Gmimj

|xi − xj |= PE

where we have used the previous definition of the total potential energy. If we now assume thatthe moment of inertia is not changing because the system is in equilibrium, we get the classic virialtheorem statement:

PE = −2KE (36)

Since E = KE + PE, we can also write E = −KE, showing that the total energy of the systemis negative (i.e. it is gravitationally bound).

19

The negative heat capacity of self-gravitating systems

This result is actually very strange from a statistical physics standpoint and here is why. Let’sdefine the temperature of a system by treating the stars as a monatomic ideal gas so

32NkT = KE = −E

Then the total energy is −3NkT/2, and the heat capacity is C = dE/dT = −3Nk/2. Thisis compared to the usual heat capacity of an ideal gas as 3Nk/2 (note that we have not beentoo rigorous here). This means that as you add heat to a gravitating system, the temperaturedecreases (and vice-virsa). For example, as a star radiates energy, it actually becomes more bound(and heats up). This is opposite from our intuition which says that if you remove energy fromsomething it should cool down.

On the other hand, if you remove energy from a star cluster (for example by removing the mostenergetic stars), then the temperature will increase, as will the kinetic energy. The potential energywill become more negative because of the virial theorem, and for a given mass, this means a smallR. So as you remove energy, the cluster shrinks and has higher velocities – it is more bound. Infact, as we will see, globular clusters can lose energy due to evaporation and the odd behaviourprescribed by the virial theorem will result in core collapse.

Measuring the mass of a system using the virial theorem

The fact that the kinetic energies and potential energies are linked gives us a way to measurethe mass of a self-gravitating system. Basically if we can measure the velocity dispersion of anelliptical galaxy or globular cluster, we can compute its mass. One difficulty is that we can usuallyonly measure the radial velocity (via the doppler shift): σ2

r =⟨v2r

⟩− 〈vr〉2. The usual solution is

to assume that the unobservable velocity dispersions in the two other (tangential) directions areequal to the radial velocity so the total dispersion is just σ2 = 3σ2

r

Then, the kinetic energy is Mσ2/2. The potential energy requires assuming some distribution forthe galaxies so that we can carry out the integral or sum for the total potential energy. If weassume that the mass is uniformly distributed in a sphere of radius R, then

PE = −3GM2

5R

For a Plummer sphere, PE = −3πGM2/32aP . The mass then can be computed through the virialtheorem. So for example, for a Plummer sphere, the mass is

M =32aPσ

2r

πG

4.4 An application of the Virial Theorem: The Tully-Fisher relation

The Tully-Fisher relation is a correlation between the galaxy’s luminosity and the maximum ro-tational velocity of the gas, often measured via the HI 21 cm line width:

L ∝ V αmax (37)

20

where α ∼ 4 (although the value appears to depend on the wavelength at which the luminosity ismeasured).

This is strongly reminiscent of the Faber-Jackson relation, implying some common origin. Becausewe are dealing with self-gravitating, equilibrium systems, with turn to the virial theorem whichprovides a relation between the kinetic energy (i.e. velocity) and potential energy (which is relatedto mass or luminosity) for such systems. The virial theorem, which can be derived from theBoltzmann equation (by first multiply by the velocity and integrating over velocities to get theJeans equation and then multiplying by position and integrating over all positions), can be statedas: W = −2K, where we define the potential and kinetic energies as:

W = −GMRg

K =12M⟨v2⟩

(38)

To relate the mass M to the luminosity L of the galaxy, we use the usual definition Υ = M/L andin adition define Cv =< v2 > /v2

max so that

L =RgCV

GΥv2max (39)

If we assume that the radius Rg is linearly related to the scale length of the disk and that all spiralgalaxies have the same surface brightness I0 so that L = πR2

GI0, then we get:

L =C2

v

πI0G2Υ2V 4

max (40)

which reproduces the scaling of the Tully-Fisher relation. While this appears successful, it hides anumber of serious problems. The first is that the surface brightness of all galaxies is not constant– in fact, the scatter in the surface brightness of spirals is several orders of magnitude. However,the Tully-Fisher relation itself is very tight and so we have created something that is more thanthe sum of its parts: the final relation has a better correlation than its individual components.

Another problem is that rotation velocity curves are set in large part by the dark matter component(because the vc curves are flat, the dark matter must dominate beyond a few disk scale lengths).This means the amount of dark matter inside a few disk scale lengths must correlate with the massof baryons. This is, at face value, a surprising result because the baryon distribution is set by itsspecific angular momentum content (i.e. when rotation balances gravity). while the dark matterstructure is presumably set by something else (e.g. the velocity dispersion of the dark matter).

Despite these difficulties, it seems likely that we are on to important element explaining thisrelation. We can apply the same virial reasoning that we just used on the Tully-Fisher relation tothe elliptical galaxies’ Fundamental plane. For example, we can again take the scalar virial theoremand define dimensionless quantities relating physical quantities to observables: Cv =

⟨v2⟩/σ2

0 andCR = Rg/Re where σ0 is the central velocity dispersion of the elliptical galaxies. This gives us

Re =CvCr

GπΥσ2

o

〈I〉e, (41)

where we have related the gravitating mass to the luminosity via the mass-to-light ratio Υ andemployed the mean surface brightness inside the effective radius defined in the section on ellipticals.

21

This bears some similarity to the Fundamental plane as we can see by taking the log of the aboveexpression and writing the surface brightness in terms of magnitudes (µ):

logRe = logCvCR

Gπ+ 2 log σ0 + 0.4µ− log Υ. (42)

The 0.4 exponent in front of µ is close to the observed 0.36, but σ20 differs quite a bit from σ1.4

0 .Possible explanations are non-homology (i.e. the structure of the halo does not scale so Cv is notreally a constant but depends on σ0), or “tilt”, an expression indicating the Υ varies with ellipticalmass (or σ0).

4.5 The potential: bumpy or smooth?

In a previous section, we showed that the total energy of a star was conserved if the potential didnot depend on time (i.e. Φ(x) rather than Φ(x, t)). In that case, a star — once bound — cannever escape from a system, and so an isolated stellar system cannot lose stars (and energy) if thepotential is time-independent. So this makes us ask the question: do realistic stellar systems havetime-independent potentials?

A related question is: what sets the potential seen be an average star: the whole mass of starscombined, or is the potential contribution from the closest star? I.e. is the potential mostlysmooth, or is it bumpy? This is related to the previous question because if the potential is setmostly by the sum of all the stars, then it will be time-independent as long as the system is inequilibrium. On the other hand, if it is set by the nearest star, that is clearly moving and so thepotential must be time-dependent. The answer, as we will see, depends critically on how manystars there are. This is perhaps not surprising since we know that in the limit of a handful of stars,the potential must be very bumpy.

4.5.1 The relaxation time

We tackle this problem by first looking at the velocity change caused by the nearby passage of onesingle other star, and then sum up this contribution for all other stars. The first part becomes atwo-body problem (one star interacting with another), which can be solved exactly. The geometryof the collision is shown in the figure below.

A star moving with velocity v encounters another star with minimum separation b (b is known asthe impact parameter). Although this can be solved exactly, we do not require the full machineryof an exact solution and instead adopt the impulse approximation, in which we assume that theforce can be calculated based on the star’s original motion. The change in velocity is applied

22

impulsively after we have made the calculation. This is a reasonable approximation as long as thecalculated velocity change is relatively small compared to the original velocity.

From symmetry, the net force in the direction of travel will be zero and so we can compute thechange in the tangential velocity v⊥. At any given instant, the tangential force is

m1dv⊥dt

=Gm1m2

b2 + x2cos θ

where m1 is the mass of the moving star, and m2 the mass of the stationary star. If we writex = vt, evaluate cos θ in terms of x and b, cancel m1 and integrate over the whole trajectory, wefind:

v⊥ =∫ +∞

−∞

Gm2bdt

[b2 + (vt)2]3/2=

2Gm2

vb(43)

The size of the deflection is large when v⊥ = v (and our approximation also breaks down at thispoint). This occurs when the impact parameter b is

bs =2Gm2

v2

This result can also be found by demanding the the potential energy Gm2/b is equal to the kineticenergy m2v

2/2 at the closest approach.

For the sun, we can evaluate this number. Setting m2 msun and v ≈ 20 km/s (this is veryapproximately the average velocity difference between stars in the local neighbourhood), then bs isless than 1 A.U., the distance between the earth and sun. It is only for approaches between starswhich are this close that the other star’s contribution to the potential overwhelms the rest of thegalaxy’s.

Clearly this is a very close approach of two stars and we suspect (and hope!) that it is an unlikelyevent. We can check this be asking what the mean free path is between such “gravitational”collisions. As before, we use l = 1/nσ, but now we take sigma to be the gravitational cross-sectionrather than the physical cross-section, so σ = πb2s. Substituting in for value of bs found before, wesee that l = v4/4πG2m2n. Equivalently we can talk about the time between collisions t = l/v andwe find that

ts =v3

4πG2m2n= 4× 1012 yr

(v

10 km/s

)3 ( m

1M

)−2 ( n

pc−3

)−1

This is a reassuringly long time (much longer than the age of the universe), although clearlyencounters which area not quite so catastrophic are still possible.

For a globular cluster, things are different because stars are much more tightly packed. In particularfor typical globular cluster densities of n ∼ 103 pc−3, the gravitational strong interaction timescaleis shorter, about 4 Gyr.

However, we have only calculated this timescale for strong encounters – those that change thevelocity by a large amount. What about the larger number of smaller encounters — are thoseimportant. We can account for all encounters by summing up the contribution from all the otherstars that a given star is expected to interact with. Each encounter will provide some changev⊥ in the star’s perpendicular velocity. On average, the mean velocity will be zero because onaverage half with be positive and half will be negative. Nevertheless, a given star will generally

23

pick up some non-zero velocity. This is just like a random walk — if you take a large number Nof random steps in one direction or another, on average you will find yourself

√N steps away from

your starting point. Therefore, we want to compute⟨v2⊥⟩, not 〈v⊥〉.

To account for all of the other encounters, we integrate over the rest of the impact parameters. Ifyou are moving with velocity b through a sea of stars, the number of stars you will encounter withimpact parameters in the range b to b+ db after a time t is nvt(2πbdb). This is just the volume ofa small ring with radius b and width db (and so area 2πbdb) moving over a length vt. The resultof integrating over all b is:⟨

v2⊥

⟩=

∫ bmax

bmin

nvt2πbdb(

2Gmbv

)2

=nt8πG2m2

v

∫ bmax

bmin

1bdb =

nt8πG2m2

vlnΛ

where we have defined Λ = bmax/bmin. Once again we are interested in how long it take to make alarge change in the velocity (at which point the bumpyness of the potential is important), so when< v2

⊥ >= v2. This is defined as the relaxation time (we shall see why this name in a moment):

trelax =v3

8πG2m2n lnΛ(44)

Notice that the time here is a factor of 2 lnΛ ∼ 40 less than the timescale from a single stronginteraction calculated before. This is due to the cumulative effect of all of the other stars whichindividually have weaker interactions but are more numerous.

What values should be taken for bmin and bmax? Clearly bmax should be roughly the size of thestellar system, since there are no stars beyond this distance. On the small size, bmin cannot beless than bs (the impact parameter at which the velocity change from a single encounter is large),because our initial impulse approximation breaks down at this point (a better calculation providesa similar result – that bmin ≈ rs). In fact, the precise value of these two parameters is not thatimportant because of the ln function. For the galaxy, bmax ≈ 30 kpc, and using bmin ≈ 1 AU ascalculated before, we find lnΛ ≈ 20.

Therefore trelax ≈ 1012 yr for the sun, still comfortably longer than the age of the universe, andwe can conclude that the potential of the Milky Way, and other large galaxies is smooth.

On the other hand, for many globular clusters, this is not the case, as typical values gives trelax ≈5× 109 yr, and even shorter for open star clusters.

On easy way to give an idea of how important this discreteness (due to the bumpy potential) isto compare the relaxation time to the cross time of the object (tcross = R/v). Using the virialtheorem, we know that KE = −PE/2, or (Nm)v2/2 ≈ G(Nm)2/2R where we have assumed thesystems are composed of N stars each of mass m (obviously an oversimplification but we’re afterrough results here). This gives

lnΛ = lnR

bs= ln

GNm

v2

v2

2Gm= ln

N

2So putting this all together we find

trelax

tcross=

v3

8πG2m2 lnN/2v

R=

N

6 lnN/2(45)

This confirms our earlier expectation that the relaxation time must be related to the number ofstars in the system. The relation is particularly simple.

24

4.5.2 The effect of relaxation: core collapse and mass segregation

We now have a way to determine for a given system, whether the potential is smooth or bumpy.Why is this important? One way of answering this question has already been alluded: a bumpypotential cannot be time-independent, and so the energy of individual stars is not conserved(although the total energy of the system is). If some star can be given enough energy that its totalenergy is positive (i.e. its velocity is larger than the escape velocity −2Φ(x) at that point), then itwill escape. Since this star has proportionally more than its share of the energy, this will decreasethe mean energy of the remaining stars. In other words, the system will lose energy. Because ofthe negative heat capacity, this will cause the system to shrink and become more bound.

The process of losing high-energy stars in this way is known as evaporation. We can be morequantitative than this simple argument (as we usually are in this course!), and work out an estimatefor the timescale for evaporation. We do this by recognizing that gravitational collisions (just likephysical ones) will randomize the direction and amplitude of the stars’ velocities. Just like theatoms in a gas, the distribution of stellar velocities will be given by the Maxwell-Boltzmanndistribution.

The Maxwell-Boltzmann distribution

The reason for this can be seen by the following argument. Given one dimensions, say the x-direction, each interaction will either increase or decrease the velocity in this direction. Given alarge number of scattering events, the distribution of velocities will quickly go to a Gaussian, witha mean x-velocity of zero and a width that depends on the amount of kinetic energy available.The distribution of x-velocities (i.e. the chance of finding a particle with velocity between vx andvx + dvx will be f(vx) ∝ exp(−v2

x/2σ2x)dvx. Similar expressions will hold for vy and vz. Since

each direction must be independent to get the joint distribution f(vx, vy, vz), we just multiply theindividual distributions together:

f(vx, vy, vz) = exp(−v2x/2σ

2x) exp(−v2

y/2σ2y) exp(−v2

z/2σ2z)dvxdvydvz

= exp(−(v2x + v2

y + v2z)/σ

2)dvxdvydvz

In the second line we have assumed that the velocity dispersion σ in each direction is equal.We can transform to a spherical coordinate system where the velocity is written in terms of thevelocity magnitude v2 = v2

x + v2y + v+ z2 and two angles. Since there is no preferred direction, the

distribution function cannot depend on these angles. In that case the velocity “volume” elementdvxdvydvz becomes 4πv2dv. The distribution then becomes:

f(v) ∝ exp(−v2/2σ2)v2dv

If we then associate σ2 with the temperature via the usual relation for a monatomic gas m3σ2/2 =3kT/2 (the factor of 3 on the left-hand side comes from the fact that σ is the 1-dimensional velocitydispersion), and we can write:

f(v) ∝ exp(−mv2/2kT )v2dv

which is the Maxwell-Boltzmann distribution for a monatomic gas with temperature T . Now wesee why we call it the relaxation time – it takes this long to “relax” to a Maxwell-Boltzmanndistribution.

25

Note also that the velocity directions will be randomized, leading to a spherical system – a non-spherical system is a good indication that relaxation has not yet occurred (fully).

Evaporation

This distribution is quite wide and in particular include velocities larger than the escape velocityve = −2Φ(x). All of these particles will escape. To find out the fraction of such stars, we need tointegrate this expression from ve to infinity. Given a potential we can calculate this as a functionof position and integrate over all positions, but we can calculate an approximate answer with thefollowing. First we compute the average kinetic energy of escape < KEescape >:

〈KEescape〉 = 〈mve/2〉 = −〈mΦ(x)〉 = − 1N

∑Φimi

In the last step we have just explicitly written out what we mean by the average of something. Butwe also recognize the total potential energy as 2PE =

∑Φimi. Using the virial theorem, which

states that PE = −2KE, then we see that

〈KEescape〉 =14KE/N =

14〈KE〉

and we see that the average kinetic energy required for escape is four times the mean kinetic energyof the stars in the cluster, or < v2

e >= 4 < v2 >= 12σ2. We can now calculate the fraction of starswhich can escape assuming they initially have a Maxwell-Boltzmann distribution by integratingfrom this velocity to v = ∞:

fescape =∫ ∞√

12σf(v)dv ≈ 1

136

This means that during one relaxation time we call lose 1/136 of the stars in the cluster, or to loseall the stars it takes about 136 relaxation times. This is the evaporation time for a cluster:

tevaporation ≈ 136 trelax (46)

Equipartition and Mass segregation

Another effect of gravitational “collisions” between stars is that they will exchange energy. Becauseof the higher inertia of more massive particles, they will tend to lose kinetic energy to less massiveparticles (assuming they both start out with similar velocities and so unequal kinetic energies).Collisions will result in a sharing of the energy such that, on average, the kinetic energies of lowmass and high mass particles are the same:⟨

12m1v

21

⟩≈⟨

12m2v

22

⟩so that the velocities will take the ratio v1/v2 =

√m2/m1. A smaller velocity dispersion will result

in particles sinking to the center of star clusters, resulting in mass segregation. In particular,this will force black holes and binaries towards the center.

Core collapse

26

These processes combined with the negative heat capacity of a cluster will lead to core collapse,the process by which a star cluster loses high-energy stars, and becomes denser and denser, partic-ularly in the core. The core also tends to have the more massive stars. The denser the system, theshorter the relaxation time, and the faster core-collapse proceeds. There are a number of globularclusters with such high central densities, and short relaxation times, that core-collapse must haveoccurred. As we have seen, (large) galaxies do not suffer from this effect.

So what stops this process eventually? The answer appears to be the formation of close binarystars. As the density increases, the chance of a three-body interaction increases, to the point thatbinaries with small separations can form (where small is defined so that the rotational velocity ofthe binary is larger than the typical velocity dispersion of the star cluster). When a third starinteracts with the binary, it tends to pick up energy and force the binary into even tighter orbit(making it more bound). This acts as a source of energy to stem the energy loss due to evaporation,and halt core-collapse.

4.6 Measuring Galactic Rotation

Stars (and gas) in spiral disk galaxies undergo (nearly) circular motion. Previously (eq. 34), wederived a relation between the circular velocity vc(R) and the total mass enclosed within thatradius:

vc =

√GM(< r)

r.

This, of course, can be used to measure the amount of mass as a function for spiral galaxies – theresult of which will be — as we will see — in conflict with the amount of visible matter observedin galaxies, and hence one important piece of evidence for dark matter.

In this section, we will discuss how the rotation velocity is actually measured, first in our galaxyand then in external galaxies.

4.6.1 In the Milky Way

Viewed from within the Milky Way, the rotation is surprising hard to measure. The basic reasonis that nearby stars are moving at basically the same velocity while more distant stars are difficultto see due to all the intervening dust. Nevertheless, we develop the machinery to determine therotation velocity from observations of other stars (or dust clouds).

We imagine the situation shown in the figure at right. The sun is a distance R0 from the galacticcenter, and moving with a circular velocity V0. We observe another star which is a distance Rfrom the galactic center and moving at velocity V . The distance between us and the other staris d, and we see it at an angle away l from the direction of the galactic center. Our two ways ofmeasuring velocities are quite different, so we decompose the velocity difference of the two starsinto the radial part, which can be measured with a Doppler shift, and the tangential part, whichshows up as observed “proper motion” on the sky. We begin with the radial part.

The radial velocity difference is:Vr = V cos θ − V0 sin l (47)

27

We can rewrite this using the sin rule (sin l/R = sinπ/2 + α/R0), and we find that,

Vr = VR0

Rsin l − V0 sin l

= R0 sin l(V

R− V0

R0

)(48)

We note that if the Milky Way as a rigid rotator so that Ω = V/R was constant than the radialvelocity different would always be zero: Vr = 0. In fact, as we will show V is nearly constantexcept in the inner parts, so Ω ∝ R−1.

Let’s take a closer look at this last equation and examine the signof the radial velocity depending on the direction we are lookingrelative to the galactic center.

(i) If 0 < l < π/2, then we are looking in the 90 degree quadrantthat is mostly toward the galactic center. For this range, sin l ispositive, and vR > 0 if R < R0 (and vR < 0 if R > R0).

(ii) If π/2 < l < π (looking away from the galactic center), thensin l is always positive and R is always larger than R0, so Vr > 0.

(iii) If π < l < 3π/2, then sin l is always negative and R is alwayslarger than R0, so Vr < 0.

(iv) Finally, if 3π/2 < l < 2π (back towards the galactic centeragain but on the opposite side), then it is the reverse of (i).

This tells us that there are certain directions in which we do notexpect to see stars (or gas) with certain radial velocities. In fact,it turns out that it is easier to compare this prediction to radiomeasurements of neutral hydrogen than anything else, largely because dust does not block our radioobservations. In particular, we can use the very low energy line that occurs due to the hyperfinetransition of neutral hydrogen (this is the transition between a state in which the electron andproton have the same spin direction, and one in which they have the opposite spin direction). Thewavelength of the photon which is emitted during this transition is 21 cm, and because of the lackof obscuration, it is not unreasonable to say that the amount of 21 cm radiation corresponds tothe amount of neutral hydrogen gas.

The gas also rotates, and we can also measure its Doppler shift. If we plot how much gas there isas a function of the radial velocity and the galactic longitude, we get the plot below (courtesy ofD. Hartmann and W. Burton).

28

First, we see that there is no emission for positive radial velocities with l in the range π/2 < l < π(i.e. between 90 and 180 degrees). Similarly there are no negative radiail velocities for 90 to 180degrees. How to make sense of the rest of the plot? Well, one way to do this would be to examinethe expected velocities from rings of hydrogen gas at various radii given what we think to be theMilky Way’s rotation velocity curve (see below). If you do this, then you would see that individualdark lines in this figure correspond to various spiral arms. In particular, arms at small radius makethe high-velocity peaks at small l. On the other hand, arms at radii large than the radius of thesun (about 8 kpc), are responsible for the ”sin” like wave seen in light-grey.

However, we can do better than this for angles pointing toward the Milky Way (i.e. −π/2 < l <π/2) using the Tangent Method. To motivate this, we go back to eq. (47), and note that for agiven angle l > 0, the most negative radial velocity will come when α = 0 (because cosα is positiveclose to α = 0). Examining the earlier figure, we see that when α = 0, this is the tangent pointof the line-of-sight along the angle l with a circle centered at the galactic center with radius R.Therefore if we can find the most negative Vr at a given angle l, we can easily find the rotationvelocity V0 that corresponds to the radius of the circle R.

We can also do the same thing for angles −π2/2 < l < 0, must this time we find the largest VR ata given angle l. The result is the rotation curve V (R) for the Milky Way for R < R0. To get therotation curve for the outer galaxy is more difficult and basically we need to use individual stars,or better yet, star clusters to find their radial velocity and distance.

We have focussed exclusively on radial velocities so far, but we can also compute the tangentialpart of the relative motion using the same logic as for the radial part. We find:

Vt = V sinα− V0 cos l

29

= R0 cos l(VR

R− V0

R0

)− V0

d

R(49)

It is generally difficult to measure tangential velocities except for very nearby stars.

Oort Constants

For nearby stars, we can derive alternate versions of the Vr and Vt equations. First, we will lookat the radial part. When d r, we can use the cosine rule to show that R ≈ R0 − d cos l, andhence

Vr ≈ d sin 2l[−R

2dΩdR

]= −2Ad sin 2l (50)

where we have defined something known as ”Oort’s constant A”. This can be measured by seeinghow the radial velocity of nearby stars varies with l, and is related to local deviation from rigidrotation (i.e. A = 0 if Ω is constant).

We can do a similar thing for the tangential part, and we find

Vt = d cos 2[−R

2dΩdR

]− d

2

[1R

d(RV )dR

]= d [A cos 2l +B] (51)

where we have also introduced Oort’s B constant. This measures the local angular momentumgradient.

4.6.2 In External Galaxies

It is both easier and harder to measure the rotation curve for external galaxies. Easier becausethere is no complicated velocity correction, and harder because they are smaller and further away.Still, there is no question that external galaxies currently give us our best data on galactic rotationcurves.

Given a rotating disk viewed from some angle i, the velocity curve is usually measured by measuringthe doppler shift in some line (usually either the 21 cm line discussed earlier, or some other lineof hydrogen). This is a difficult observational disk, but done correctly it gives us the followinginformation:

Vr(R, i) = Vsys + V (r) sin i cos θ

We are after V (r) and so need to correct for the inclination angle of the galaxy (i, which usuallycan be determined to an accuracy of a few degrees) and the systematic velocity of the galaxy.

The result of doing such an observation is shown below for the large spiral galaxy NGC 3198(figure from Van Albada). This is typical for large spirals, including our own Milky Way in thatthe rotational velocity rises steeply at small radius, and then is mostly (but not perfectly) constantafter that.

30

This figure also shows an attempt to show the contribution of the stellar disk to the rotationvelocity. Since the velocity curve is related to the mass enclosed, with can write:

v2c =

G

R(Mdisk(< r) +Mhalo(< r))

The contribution to the disk mass comes from integrating over the distribution of stars, whichpeaks around 5-10 kpc. Because the rotation curve remains flat after that we must posit eithersome form of dark matter (the usual solution), or modify the equations of Newtonian gravity.

Notice that the dark matter distribution is more extended. The composition of the dark matterremains unknown.

Finally, we should point out that the smaller galaxies show a more slowly rising velocity curve.Such galaxies also appear to be more dark matter dominated than large spirals.

4.7 Spiral Structure

One of the most intriguing questions about spiral galaxies is how and what are the spiral arms.It seems very unlikely that they are fixed physical structures because the disk is differentiallyrotating: the outer parts have a lower angular velocity (Ω = vc/R) than the inner parts, causingany physical spiral structure to wind up on a timescale of the orbital time of the galaxy, which istypically a few hundred million years, much lower than the age of the entire system (the orbitalperiod T = 2π/Ω). This is known as the winding problem.

Instead, the prevailing idea behind spiral structure rests on spiral density wave theory. Thisdescribes the (spiral) wave patterns that result from perturbations in self-gravitating stellar disks.Our basic idea is that the natural mode of vibration for a differentially rotating self-gravitatingsystem is spiral waves. There have been a wide variety of other theories, such as magnetic fields

31

and self-propagating detonation waves, and interested readers can read Binney and Tremaine fora longer discussion on this topic. One key reason for this is the observation that spiral waves areseen in all stellar populations and so seem to represent a perturbation to the potential of the disk,and do not just result from changes in the star formation in spiral arms (although it is clear bythe large number of young stars in spiral arms, that star formation preferentially happens in theseareas).

4.7.1 Epicycles: nearly circular orbits

Spiral arms are observed in disks made out of stars which are in (nearly) circular orbits. Starsin orbits which are nearly, but not quite, circular can be described as perturbations on top of acircular orbit. Here, we develop a linear evolution equation for the deviation of the orbit fromcircular. The acceleration of a star is described by Newton’s equation: r = −∇φ. In cylindricalcoordinates with radius R, azimuthal angle φ and height z, this can be written as:

R−Rφ2 = − ∂φ∂R

d

dt

(R2φ

)= 0

z = −∂φ∂z

These are the R, φ and z components respectively, where we have assumed the disk potential isaxisymmetric (i.e. φ(R, z) is a function of only R and z). The middle equation is an expression ofthe conservation of angular momentum in the z-direction: Lz = Rvc = R2φ is a constant. We canuse this definition to re-write the first equation as:

R = − ∂φ∂R

+∂

∂R

(L2

z

2R2

)= −∂φeff

∂R

which we have re-written in terms of an effective potential φeff = φ+ L2z/2R

2. The exact form ofthis effective potential depends on the potential well of the disk, but has a minimum at the radiusRc of a circular orbit with angular momentum Lz. Since we are looking for small perturbationsaway from this position, we can perform a Taylor series expansion around the point Rc, definingthe distance away from Rc as x = R−Rc:

φeff =12∂2φeff

∂R2x2 +

12∂2φeff

∂z2z2 + higher order terms

Note that we have dropped the ∂φ/∂R and ∂φ/∂z terms because the unperturbed orbit is at aminimum in the potential (and the constant term can be set to zero because it has no physicalmeaning anyway). Putting this into the equation for R (similar results apply for z), and notingthat R = x, we find:

x = −κ2x (52)

which describes simple harmonic motion with a frequency known as the epicyclic frequency:

κ2 =∂2φ

∂R2+

3L2z

R4c

(53)

32

From the definition of Ω, we note that

Ω2(R) =v2c

R2=

1R

dΦdR

which lets us write κ asκ2 =

d(RΩdR

+ 3Ω2 = −4BΩ (54)

where in the last step we have related this to Oort’s constant B (defined earlier). We note that ingeneral κ 6= Ω, meaning the orbital frequency is not equal to the frequency of oscillations in theradial direction.

The epicyclic approximation is useful because it describes the timescale for typical non-circularperturbations to oscillate (or grow) in the radial direction of a disk.

What does the epicyclic motion look like?

The radial motion (around the guiding radius Rc) is given by the solution to eq. 52:

x(t) = X cos(κt+ ψ)

where X is a constant which depends on how large the perturbation is. This only describes theradial oscillations as the star orbits — to find out the whole shape we also need to know what theazimuthal oscillations look like. We can find this out by noting that Lz must be constant for thestar, even as it oscillates. Since Lz = R2dφ/dt, we can write

dφ

dt=Lz

R2=

R2cΩc

(Rc + x)2

where Ωc is the rotation velocity of the unperturbed orbit (with radius Rc). In the second step,we have used the definition of x = R − Rc. Since we have already assumed that x Rc, we canrewrite this as

dφ

dt= Ωc

(1 +

x

Rc

)2

≈ Ωc

(1− 2x

Rc

)Substituting in for the solution for x, we can integrate this to find

φ(t) = φ0 + Ωct−2ΩXRcκ

sin (κt+ ψ)

The first term is just a constant of integration, the second term represents the primary orbitalmotion, so the third term is the oscillation we are interested in. In order to get a better idea of theshape of the oscillation, we define the variable y = Rcφ to be orthogonal to x in the, and (focusingonly on the oscillation term), we find

y(t) = −2ΩXκ

sin (κt+ ψ)

Taking x and y together, we see this is the formula for an ellipse with a (long) y-axis which is 2Ω/κtimes larger than the shorter axis. Also the rotation is retrograde in the sense that the oscillationgoes around its little ellipse in the opposite sense as the main orbit.

For the solar system, Ω ∝ R−3/2, so κ2 = −3Ω2 + 4ω2 = ω2, and the rotational frequency isthe same as the epicyclic frequency. This means that a star completes exactly one radial epicycleoscillation for every one orbit around the central object, or, in other words, the orbit is closed (i.e.it returns exactly to the same spot). Also, the amplitude of the y-oscillation is exactly twice thex-oscillation.

33

4.7.2 Building spiral arms from epicycles

For galaxies, Ω 6= κ in general, and orbits are not closed. Actually, this is not quite true – if wethink about it carefully we realize that if the star can do two radial oscillations during one orbit,it will close back on itself. In fact, if the ratio of Ω/κ is a rational number, then the orbit willeventually close.

More generally, the ratio of Ω/κ is not rational, and the orbit doesn’t quite close, and instead thepoint where the radial motion returns to its original position is some constant angle δθ ahead orbehind of the starting angle. If we look at the system in a frame which is rotating at a speedsuch that we move this angle in one rotation of the circular orbit (i.e. at a frequency given byΩp = Ω− nκ/m where n and m are integers), then the orbits do appear to close.

Therefore if we can arrange the orbits to create a pattern (in particular a spiral pattern), at oneepoch then this pattern will rotate with a frequency given by Ωp above. In the figure below, weshow a number of shapes built out of various closed orbits.

Of course, this only works if Ωp is independent of R so that the pattern at all radii moves with thesame angular frequency. Remarkably, for typical spiral galaxy rotation curves this is true over awide range of radii for selected values of n and m. In particular, for n = 1 and m = 2 this holds,so that Ω(R)− κ(R)/2 depends on slightly on radius (for a range of radii).

This discussion is purely kinematical, it does not take into account the fact that the axisymmetricperturbations (i.e. the spiral pattern) will change the potential and so modify the result. However,a more detailed investigation shows that a process known as swing amplification can actuallyhelp grow a small spiral pattern into a more pronounced one. The self-gravity of the spiral per-turbation is probably also important in resisting the slight residual winding problem that comesfrom the fact that Ω− κ/2 is still not perfectly flat.

While this gravitational effect is clearly important in many real galaxies, it is also quite likely thatthe visibility of spiral arms is enhanced by other physical processes, including the increased starformation created by the density enhancements.

4.8 Galaxy Interactions I: Dynamical Friction

As we discussed earlier, galaxies are often found in groups or clusters. In addition, of course,galaxies are surrounded by smaller dwarf galaxies and globular clusters. This leads to interactionsbetween galaxies. In this section and the following two, we will explore the physics of theseinteractions. We will begin with the drag force caused by a galaxy or satellite moving through abackground of stars, and then move on to tidal interactions before discussing the impact of actualmergers of two systems.

34

Review of galaxy groups

First, we briefly review the observations of galaxy grouping. We will divide this (somewhat arbi-trarily) into three divisions:

Galaxy clusters are the largest observed congregations of galaxies, with typical large clustersshowing several thousand bright galaxies within a sphere with radius of about 2000 kpc (2 Mpc).The mass (as determined from virial arguments) of such objects is about 1015M. Most (85%) ofthis mass is dark, in that we have only gravitational evidence of its existence. A minority (a fewpercent) is contributed by stars, while the rest is even distributed within the cluster in the form ofa hot gas. The temperature of this gas is as high as 108K and emits primarily in the X-ray band (infact galaxy clusters are also known as X-ray clusters). The temperature of the gas can be derivedeasily through virial arguments (i.e. 3kT ∼ GM/R). The velocity of the galaxies is also very largeand the velocity dispersion is measured to be thousands of km/s. This makes interactions, whenthey occur, very fast.

Galaxy Groups are scaled down clusters in that they are very similar but have only 10-100galaxies, and have masses of around 1013M, with radii around 600 kpc. Many of these systemsare also observed to have hot gas evenly distributed within the group, although fractionally lessof the regular matter (i.e. not dark) is in the from of gas, and more is in stars (as compared toclusters). The velocities are typically 400-500 km/s, and the gas temperature is around a few times106 K.

Finally, as we have discussed earlier, individual galaxies such as the Milky Way have extensivesatellites. These satellites are typically much less massive and much less bright, but the MilkyWay is thought to have about 30 satellites, with more certainly to be discovered. As we havediscussed, much of the mass in spiral galaxies is dark, and the rotation velocity is about 200 km/s.The satellites of the Milky Way (like the LMC and the SMC) orbit with velocities of this orderand distances around 20-100 kpc. There are also a few hundred globular clusters.

Dynamical Friction

Galaxy interactions are certainly important in all of these systems, but one important effect is easyto overlook. As a satellite moves through a background of stars or dark matter particles, it hasmany smaller encounters with these objects. Because there masses are much smaller, the impact isvery small, but if there is a sufficiently large number of such small stars or dark matter particles,then the cumulative effect can be very large. This effect turns out to have a frictional effect –slowing down the larger galaxy satellite as it passes by. This processes is known as dynamicalfriction.

In an earlier section, discussing the effect of individual stars’ contribution to the potential, wederived a relation for the change in the tangential velocity due to the gravitational force of anearby star. This result (eq. 43) was found by applying the impulse approximation and is givenby

v⊥ =2Gmbv

where b was the impact parameter. Although we did not discuss this point earlier, the other star(with mass m) must gain an equal and opposite momentum according to Newton’s third law. Thisstar will have a perpendicular velocity of −2GM/bv. Notice that if the galaxy has a mass M whichis much larger than the star’s mass m, then the star will get most of the kinetic energy. The total

35

kinetic energy due to the motion perpendicular to the galaxy’s motion is

∆KE⊥ =M

2

(2Gmbv

)2

+m

2

(2GMbv

)2

=2GMm(M +m)

b2V 2

Long after the collision the total amount of kinetic energy must be preserved. Since we haveincreased the kinetic energy in the perpendicular direction (which was zero to begin with by def-inition), we must have decreased the kinetic energy in the parallel direction. In other words, wemust have slowed down the motion of the galaxy. This appears to be at odds with our impulseapproximation calculation, which seemed to show that there was no net force in the parallel direc-tion. In fact, of course, the galaxy or star moves somewhat and this invalidates the approximationsomewhat. Still, our basic result will be approximately correct.

Kinetic energy conservation tells us

M

2V 2 = ∆KE⊥ +

M

2(V + ∆V‖)

2 +m

2

(M

m∆V‖

)2

If, as we have specified for a weak encounter, ∆V‖ V , then we can drop all the ∆V 2‖ terms.

Multiply out the previous formula, canceling the MV 2/2 terms, and using this approximation, wefind

∆V‖ = −KEMV

= −2G2m(M +m)b2V 3

This is change in the velocity due to the interaction with one star with impact parameter b, Toaccount for the effect of all stars, we integrate over all impact parameters as we did before:

dV

dt= −

∫ bmax

bmin

nV2G2m(M +m)

b2V 32πbdb

= −4πG2(M +m)V 2

nm lnΛ (55)

These result demonstrates two key points:

(i) The sign is negative so it is a fractional force. This comes about because each star or darkmatter particle tends to slow the galaxy down.

(ii) The effect is proportion to v−2, so that the effect is larger as the velocity gets smaller (up toa point – if v is too small, then are original impulse approximation breaks down).

Impact of Dynamical Friction

Let us now consider the role of dynamical friction as a satellite galaxy orbits a larger system. Evenif the separation is too large for the satellite to be moving through the stellar field of the largergalaxy, it will be moving through a field of dark matter particles (our analysis applies equallywell to this case). In fact we note in the above expression that the amplitude depends on thecombination ρ = nm so that it is the density of stars or particles, and not the individual masseswhich is important. As the satellite orbits, it loses energy due to the dynamical friction, and sothe orbital radius decreases. This will cause the satellite to slowly spiral in towards the center ofthe galaxy, and may eventually cause a merger.

36

If we now assume that the satellite galaxy is on a circular orbit within a larger host galaxy, wecan replace the velocity with the circular velocity of the host (v2 = GMtotal/R):

dV

dt= −4πGRnm

M

MtotallnΛ

This demonstrates a third important point:

(iii) The important of dynamical friction increases with the ratio of the satellite mass to the massof the host galaxy. This means that it is unimportant for a single star, but becomes increasinglyimportant as the satellite mass approaches the central galaxy’s mass.

The result we just derived is useful, but it depends on the density of the dark matter particles. Wecan adopt a model for how the dark matter is distributed as a function of radius, which will allowus to develop a simpler expression (albeit one which depends on our model of how dark matter isdistributed). The simplest approximation for the dark halo is a spherical isothermal sphere model,for which,

ρDM(r) =v2c

4πGr2

In this case, the result is particularly simple:

dV

dt= −GM

r2lnΛ

To find how a galaxy’s radius evolves with time, we can again assume a circular orbit and useeq.(31) to find an expression for the specific angular momentum l = L/M of the galaxy:

dl

dt= −GM

rlnΛ

If we then assume that the circular velocity is constant, we obtain

rdr

dt= −GM

vclnΛ

which can be solved for the time take to sink to the center of the halo from some initial radius ri.We find this dynamical friction timescale to be:

tfric =r2i vc

GM lnΛ=

2.6× 1011yrlnΛ

(ri

2kpc

)2 ( vc

250km/s

)(M

106M

)−1

.

We can evaluate this for a few cases of interest. For example, in globular clusters with parametersas indicated in the above formula, the time scale is (for ln Λ ≈ 20) of order 10 Gyr, which makes itonly important for the most massive globular clusters, or those closest to the center of the galaxy.

Another example is the Large Magellenic Cloud (LMC), which has a mass of about 1010M and aradius of about 60 kpc. This corresponds to a dynamical friction timescale of a few Gyr, and so wepredict that relatively soon the LMC will merge with our own galaxy. In fact, the recently detecteddwarf galaxy in Sagittarius has almost surely already suffered this fate and is in the process ofbeing tidal disrupted (see the next section).

Finally, we can compute the same time for galaxies within groups and clusters. In this case, wefind that because of the mass ratio argument (point (iii) above), dynamical friction is importantfor galaxies within groups and possibly small clusters, but not for the largest clusters we see.

37

4.9 Galaxy Interactions II: Tidal effects

Once a satellite galaxy has been brought close enough through the action of dynamical friction(or simply due to a very close passage), it can lose stars, gas and dark matter due to the strongergravitational pull of the larger object. This can actually be seen occurring in globular clusters anddwarf galaxies close to the Milky Way, as well as larger galaxies in groups and clusters.

In order to develop the mathematics for treating tidal effects generally we will consider the so-called restricted 3-body problem in which we examine the motion of a test particle due to theimpact of both the main galaxy and the satellite, under the approximation that the satellite isundergoing circular motion around the larger galaxy and the test particle has no impact on theother systems. For a star orbiting a satellite, this condition is easily fulfilled.

We will approach this problem by computing an effective potential, as we did for the near-circularorbits. In this case, however, the effective potential will be two-dimensional, rather than justdepending on the radius. To do this, we will transform the usual equations of motion into acoordinate system which is rotating with the circular motion of the satellite. In this case, thesatellite will appear stationary, making the effective potential time-independent. The down sideof this transformation will be the introduction of fictitious forces due to the non-inertial rotatingframe.

We define two frames, S which is stationary and S′ which is rotating with fixed angular frequencyΩ. At a particular instant the x and y axis of these two systems overlap. The velocity in therotating frame is related to the velocity in the stationary frame v by:

dxdt

=dx′

dt+ Ω× x

To find the equations of motion in the new frame we differentiate this expression to find

d2x

dt2=

d

dt

(dx′

dt

)+ Ω× dx

dt

=d2x′

dt2+ Ω× dx′

dt+ Ω×

(dx′

dt+ ω × x

)=

d2x′

dt2+ 2Ω× dx′

dt+ Ω× (Ω× x′)

so the equation of motion changes from the simple dv/dt = −∇Φ to

dv′

dt= ∇Φ(x)− 2Ω× v′ − Ω× (Ω× x′)

The second term on the right-hand side is the Corolis force which is perpendicular to the directionof motion, and the third term is the centrifugal force. They are both fictitious forces, resultingonly from the fact that we are working in a rotating coordinate system.

As before, we would like to define an effective potential which brings us back to our simple equationof state. In this case, however, it is not possible because the Coriolis force cannot be written asthe gradient of an effective potential. The best we can do is define an effective potential as

Φeff(x′) = Φ(x′)− 12(Ω× x′)2

38

and this allows us to write the equation of motion in the simplified form:

dv′

dt= −∇Φeff − 2Ω× v′

This is not as bad as it seems because the Coriolis force is perpindicular to the velocity and so itcan do no work on the particle. In fact, we can define an energy-like quantity:

EJ =12(v′)2 + Φeff(x′)

which is conserved in the rotating frame. Note that EJ = E −Ω × L and so is a combination ofthe energy and the angular momentum (neither of which are conserved in this frame separately).

The effective potential: The five Lagrange points

When the gradient of the effective potential is zero, the acceleration is also zero and if a particle isplaced at this position with zero velocity, it will always stay there. These are known as stationarypoints, and it turns out that the effective potential we have written has five of them, known as thefive Lagrange points. An image of the effective potential for the Sun-Earth system is shown below.

There are three points which are on the line connecting the two objects (here the Earth and thesun), these are L1, L2 and L3. It turns out that none of these points are stable in the sense thatif you displace the particle slightly from the stationary point it will move away from that pointfaster and faster. The points L4 and L5 are stable (due to the Coriolis force).

We can write a simplified expression for the effective potential along the line connecting the twobodies. If we define x as the distance along this line from the smaller body and D as the distancebetween the two bodies, then

Φeff(x) = − GM

|D − x|− Gm

|x|− Ω2

2

(x− DM

M +m

)2

39

The stationary points can be found by setting dΦeff/dx = 0. In the limit that x D, we can findthat two of these points are at:

x = ±rJ = D

(m

3M +m

)1/3

This is known as the Jacobi radius, or the Roche lobe (for stellar systems). Stars outside of thisradius are no longer bound to the satellite and so become stripped off and start to orbit the largerobject rather than the satellite. This is known as tidal stripping.

As stated earlier, tidal stripping has affected a number of globular clusters and dwarf galaxies inthe Milky Way.

If the orbit is not circular, than this analysis is not correct, but appears to be a reasonableapproximation applied at the point of closest approach (the pericenter).

4.10 Galaxy Interactions III: Mergers

The ultimate stage of galaxy interactions is a complete merger. Mergers are one of the mostimportant driving forces in galactic evolution, but unfortunately will not be will covered in thesenotes, largely because there are few simple results to be derived. We generally learn about mergerseither from observations or from full-scale numerical simulations.

There is one simple thing we can say about mergers, which is that because stellar systems are notrigid objects, they do not act like inelastic scattering events. In particular, the motions of stars(and dark matter particles) within a system absorb some of the energy during a passage. Thisleads to a heating of the stars and a decrease in the relatively kinetic energy, increasing the changesof a merger. We can see how this works very roughly using the virial theorem.

If the total kinetic and potential energies of one galaxy before the collision are KE0 and PE0,then the total energy of that galaxy will be

E0 = −KE0

due to the virial theorem. During a close passage of two stellar systems, energy is added (takenfrom the potential energy of the two systems), and so E1 = E0 + ∆KE, where ∆KE is the addedkinetic energy. After a certain amount of time, the galaxy will readjust to match the virial theorem,and the potential energy will become less negative (by 2∆KE) and the kinetic energy less positive(by ∆KE). Since PE ∝ GM2/R, this implies an increase in R.

We can classify mergers into minor and major. Minor mergers usually involves satellites withinonly 10% or less of the mass, and generally do not lead to large-scale changes in the larger galaxy(although it still does add kinetic energy, which can thicken the distribution of stars in the disk).Major mergers are much more spectacular, particularly between two spiral galaxies and do resultin wholesale rearrangement of the matter.

In detail, spiral mergers are complicated due to resonant interactions between the orbit of starswithin the galaxy and the motion of the other galaxy. For example, a prograde encounter (in whichthe perturbing galaxy moves past in the same direction as the stars rotate), some stars will feel anextended period of acceleration and can be pulled out to large distances. These “tidal tails” areobserved in a number of spiral interactions.

40

In the final stages of a major involve a processes known as violent relaxation during whichthe potential change quickly with time. During such changes, the energy of individual stars canstrongly fluctuate, and generally stellar orbits are mixed up, resulting in a much more sphericaland isotropic system. Indeed, simulations shown that the end product of two spiral galaxies looksgenerally like an elliptical system and this is thought to be one of the major ways to form ellipticals.

41