Lesson: Adding & Subtracting Functions

It will be important for you to have a good understanding of the properties of the functions discussed in this course Polynomial Rational Trigonometric Logarithmic Exponential

Knowing your Trig Identities and Log Laws will also be beneficial

Example 1

Your summer job pays you $10/hour and the government taxes you 15% of your hourly pay for each hour you work. Determine your net pay if you work… 10 h 15 h 20 h 25 h 30 h 35 h 40 h

Example 1: Solution

# Hours Gross Pay Taxes Net Pay = Gross - Tax

10

15

20

25

30

35

40

Your gross pay is simply the # hours you work multiplied by 10 (your hourly rate)

100

150

200

250

300

350400

Your taxes are calculated by multiplying your gross pay by 0.15 (15% taxes)

15

22.5

30

37.5

45

52.560

Your net pay is the difference between these

85

127.5

170

212.5

255

297.5340

Example 1: Solution If we had decided to work with functions instead of

jumping right into the calculations, we could have saved some time:

Let the gross pay function be G(t):G(t) = 10t

where t is the number of hours worked

Let the taxes be T(t):T(t) = 0.15×10t = 1.5t

Let the net pay function be N(t):N(t) = G(t) – T(t) = 10t – 1.5t = 8.5t

Example 1: Solution

# Hours Net Pay

10

15

20

25

30

35

40

85

127.5

170

212.5

255

297.5340

Now we calculate the net pay by multiplying the number of hours worked by 8.5:

We have the exact same values as before and saved time by not having to calculate the gross pay and taxes

Example 1: Notes

Combining functions using arithmetic can be a huge time-saver when numerous calculations are necessary and/or when working with sophisticated functions

The Superposition Principle

The superposition principle states:

The sum of two or more functions can be found by adding the y-coordinates of the functions at each identical x-coordinate

Example 2

(a) Use the superposition principle to add/subtract the two functions specified by the table of values

(b) State the domain of the resulting functions

x f(x)

1 52 103 154 205 256 308 359 4010 45

x g(x)

1 1

2 3

4 5

6 7

7 9

8 11

10 13

Example 2: Solution As the superposition principle states, we can

only add/subtract the functions at identical x-coordinates

x f(x)

1 52 103 154 205 256 308 359 4010 45

x g(x)

1 1

2 3

4 5

6 7

7 9

8 11

10 13

x f(x) + g(x) f(x) – g(x)

1 5 + 1 = 6 5 - 1 = 4

2 10 + 3 = 13 10 - 3 = 7

4 20 + 5 = 25 20 - 5 = 15

6 30 + 7 = 37 30 - 7 = 23

8 35 + 11 = 46 35 – 11 = 24

10 45 + 13 = 58 45 - 13 = 32

Example 2: Solution

Because we’ve been given tables of values, the domain is simply a list of the x-coordinates :

Domain

f(x) {x/1,2,3,4,5,6,8,9,10}

g(x) {x/1,2,4,6,7,8,10}

f(x) + g(x) {x/1,2,4,6,8,10}

f(x) - g(x) {x/1,2,4,6,8,10}

Example 2: Notes Notice that not all of the points on f(x) and

g(x) are used to make f(x) + g(x) and f(x) – g(x)

The points that make up f(x) + g(x) and f(x) – g(x) occur only where f(x) and g(x) have the same x-coordinates Superposition principle

As a result, the domain of the sum or difference of functions is comprised of only those x-values that are common to the functions

Example 3 Consider the graphs

of f(x) and g(x) given below

Use the superposition principle to graph (a) f(x) + g(x) (b) f(x) – g(x)

f(x)

g(x)

Example 3: Solution

Choose an x-coordinate and then add the y-coordinates of f(x) and g(x)

f(x) + g(x)

(a)

Example 3: Solution

Choose an x-coordinate and then subtract the y-coordinate of g(x) from the y-coordinate of f(x)

(b)

f(x) - g(x)

Example 3: Notes

Notice that f(x) – g(x) has an x-intercept at x = 3, which is the point of intersection between f(x) and g(x)

At this point, the y-coordinates are equal. Therefore, their difference is zero

This holds true for all functions The x-intercepts of f(x) – g(x) occur where the function is equal

to zero: f(x) – g(x) = 0

f(x) = g(x)

And, by definition, the point of intersection is a one that satisfies f(x) = g(x)

The zeroes of f(x) – g(x) (or g(x) – f(x) for that matter) correspond to the points of intersection between f(x) and g(x)

Example 4

For each pair of functions, determine: (i) f(x) + g(x) (ii) f(x) – g(x) (iii) g(x) – f(x)

(a)f(x) = x3 + x2 – 2, g(x) = x2 – 4 (b)f(x) = log x, g(x) = log 2x(c)f(x) = sin2x, g(x) = cos2x

Example 4: Solution

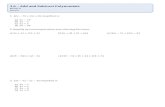
(a) f(x) = x3 + x2 – 2, g(x) = x2 – 4

f(x) + g(x) =

f(x) - g(x) =

g(x) - f(x) =

(x3 + x2 – 2) + (x2 – 4)

(x3 + x2 – 2) - (x2 – 4)

= x3 + 2x2 – 6

= x3 + x2 – 2 – x2 + 4

= x3 + 2

(x2 – 4) - (x3 + x2 – 2)

= x2 – 4 – x3 – x2 + 2

= -x3 – 2

Collect like terms

Example 4: Solution

(b) f(x) = log x, g(x) = log 2x

f(x) + g(x) =

f(x) - g(x) =

log x + log 2x

= log[(x)(2x)]

= log(2x2)

log x - log 2x

log2

x

x 1

log2

Use Product Log Law

Use Quotient Log Law

Example 4: Solution

g(x) - f(x) = log 2x - log x 2

logx

x

log 2

Example 4: Solution

(c) f(x) = sin2x, g(x) = cos2x

f(x) + g(x) =

f(x) - g(x) =

g(x) - f(x) =

sin2x + cos2x

= 1

sin2x - cos2x

cos2x - sin2x

Use Pythagorean Identity

Example 4: Notes

As this example shows, f(x) – g(x) is NOT always equal to g(x) – f(x)

In fact, it is uncommon for f(x) – g(x) to be equal to g(x) – f(x)

Example 5

Students at TASS are selling T-shirts to promote school spirit. There is a fixed cost of $210 for producing the t-shirts, plus an additional cost of $5 per t-shirt made. The students have decided to sell the shirts for $8 each

(a) Write an equation to represent the total cost of producing the t-shirts as a function of the number sold

(b) Write an equation to represent the students’ revenue as function of the number sold

(c) Identify the break-even point

(d) Determine an equation for their profit function

Example 5: Solution

(a) The cost of the shirts depends on:The fixed production cost of $210The cost of the shirts ($5 for each shirt

sold)

So, if we let n represent the number of shirts sold, the cost function C(n) becomes:

C(n) = 210 + 5n

Fixed cost of $210 Total cost resulting

from the number sold

Example 5: Solution

(b) The revenue depends on:Sales from the shirts ($8 for each shirt

sold)

So, again using n to represent the number of shirts sold, the revenue function R(n) becomes:

R(n) = 8n

Total revenue resulting from the number sold

Example 5: Solution

(c) The break even point occurs where R(n) and C(n) intersect. Graph the two functions on the same axis and see where they cross:

The two lines intersect at (70, 560)

So, the students need to sell 70 t-shirts to break even

And they will need to earn $560 revenue to balance the cost

Example 5: Solution

(d) The profit made by the students is the revenue generated less the cost of the shirts:

P(n) = R(n) – C(n) = 8n – (210 + 5n) = 8n – 210 – 5n = 3n – 210

Note: To break-even means no profit is made. So, we could solve P(n) = 0 to get the break even point. I’ll leave it to you to verify that this occurs when

n = 70, as in part(c)

Summary We can combine two or more functions using addition or

subtraction Can be done using…

Table of values Graphs The equation of the functions

The superposition principle states that the sum/difference of two functions can be found by adding/subtracting the y-coordinates at identical x-coordinates

The domain of a function that is the sum or difference of functions is the domain common to the original functions

The zeroes of f(x) – g(x) correspond to the points of intersection between f(x) and g(x)