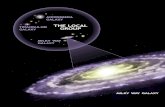
Lecture 19: The Milky Way Galaxy

Local Standard of Rest

actual (example) orbit of Sun

need better reference frame for other stars’ motion

imaginary star on circular orbit at Sun’s currentposition, LSR = mean motion of disk material in solar neighborhood

Local Standard of Rest in Cylindrical Coordinates velocities

positions

vLSR = (0, 220, 0)

v! = (−10.4, 14.8, 7.3)

vLSR = (Π0,Θ0, Z0)

relative to LSR

what does this mean?

Sun at position of LSR, but not at its speed

Differential Rotation

Oort analysis

orbital speed

angular velocity

Θ(R) =

�GM(R)

R

�1/2

ω(R) = Θ(R)/R

at Sun’s location, angular velocity = 220 km/s / 8 kpc

vr = Θ cos α − Θ0 cos(90◦ − l) = Θ cos α − Θ0 sin l

vr = (Θ

R−

Θ0

R0

)R0 sin l or vr = (ω − ω0)R0 sin l

eliminate α (which can’t be measured) using trig:

1) Keplerian rotation, 2) constant orbital speed, 3) rigid-body rotation: how do M, Θ, and ω scale with radius?

vt = Θ sinα − Θ0 cos l

eliminate α using trig:

vt = (ω − ω0)R0 cos l − ωd

for d << R_0, simplify by Taylor expanding ω:

ω(R) ≈ ω(R0) +dω

dR|R=R0

(R − R0)

equations define Oort’s constants A & B

vr ≈ R0(dω

dR)R=R0

(R − R0) sin l

R − R0 ≈ −d cos l

also

finally

vr ≈ Ad sin 2l where A ≡ −

R0

2(dω

dR)R=R0

local disk shear, or degree of non-rigid body rotation (from mean radial velocities)

vt ≈ d(A cos 2l + B) B ≡ A − ω0where

local rotation rate (or vorticity) from A and ratio of random motions along rotation and (larger) toward center

get local angular speed (A-B), therefore distance to Galaxy center, rotation period of nearby stars, thus rotation curve

for d << R_0

Cepheid radial velocities vs. l

Cepheid proper motions vs. l

1.5 kpc

3 kpc

(R < 2 kpc)

0 180

Period - Luminosity Relationship (Large Magellanic Cloud)

early 1900’s

1960’s

We can apply Oort’s equation to get rotation curve.... but there’s dust!

use HI (neutral hydrogen) instead of stars

reminder... 21 cm radiation (1420 MHz)

every ~10 Myr, electron flips its spin

sun

galactic center

can also invert this to get distances

8 kpc

Nucleus of Galaxy8 kpc away

28 magnitudes of extinction in optical

2 magnitudes in near IR

with adaptive optics

n* ~ 10^7 pc^-3

locally, n* ~ 0.1 pc^-3

Sag A (20 cm observations)

50 pc across

synchrotron emission

zoom in to Sag A West (6 cm)

rotating 5 pc spiral of ionized gas

spectrum like HII region

center of Sag A West is Sag A* (aka Sag A star)

6 AU size

proper motion is Sun’s reflex motion -- meaning?

variable (< 1 hr) X-ray source, size ~ 1 light-hr

bolometric luminosity ~ 10^3 L_sun

what is it? supermassive BH (does not result from massive star collapse alone)

Stellar Orbits

M_BH = 3.7 x 10^6 M_sun

R_Sch = 0.07 AU

could grow via accretion of 1 solar mass per 1000 yr

The Halo

stars (distinguished by kinematics and/or chemical abundances)

globular clusters

Satellite Galaxies

Magellanic Clouds

sagittarius dwarf

draco

Galaxies

(not all types included here)

Ellipticals

Ellipticals

Surface Brightness Profiles

deVaucouleurs’ profileor r^1/4 profile

Σ(r) = Σ(0)exp(−bn[(r/re)1/n

− 1]) Sersic profile

r_e is the effective radius (half light)

very little cold gas or dust in ellipticals

a few exceptions...

there is hot, x-ray emitting gas...

Prolate, Oblate or Triaxial?

what determines the shape?

difficult to tell in projection,but statistical surveys of surface brightness profiles suggest triaxial

Internal Kinematics

+

=

rotation

random

E’s

complex orbit families

support comes from rotation and/or velocity dispersion

origin of flatness?

rotation (no)

anisotropic velocitydispersions (yes)

unlikely that two axeshave same velocity dispersions --- > triaxial

Stellar Populations