Fachberichte INFORMATIK - Landau · edged inferential apparatus, where the inferential activity is...

TABLEAUX 2005Position Papers and Tutorial

Descriptions

Bernhard Beckert

12/2005

FachberichteINFORMATIKISSN 1860-4471

Universitat Koblenz-LandauInstitut fur Informatik, Universitatsstr. 1, D-56070 Koblenz

E-mail: [email protected] ,

WWW: http://www.uni-koblenz.de/FB4/

Preface

This volume contains the position papers presented at the International Con-

ference on Automated Reasoning with Analytic Tableaux and Related Methods

(TABLEAUX 2005) held September 14–17, 2005 in Koblenz, Germany. This con-ference was the 14th in a series of international meetings since 1992 (listed on thenext page). It was part of the International Conference Summer Koblenz 2005,which included conferences covering a broad spectrum of topics and interest-ing fields of application for tableau-based methods: artificial intelligence (KI),multi-agent systems (MATES), automated reasoning and knowledge represen-tation (FTP), and software engineering and formal methods (SEFM).

The Program Committee of TABLEAUX 2005 received 46 submissions from16 countries. After each paper was reviewed by three referees, and an intensivediscussion on the borderline papers was held during the online meeting of theProgram Committee, 18 research papers, 7 system descriptions, and 3 positionpapers were accepted based on originality, technical soundness, presentation, andrelevance. I wish to sincerely thank all the authors who submitted their workfor consideration. And I would like to thank the Program Committee membersand other referees for their great effort and professional work in the review andselection process. Their names are listed on the following pages.

In addition to the contributed papers, the program included four excellentkeynote talks. I am grateful to Prof. Diego Calvanese (Free University of Bolzano,Italy), Prof. Ian Horrocks (University of Manchester, UK), Prof. Hans-JurgenOhlbach (Ludwig Maximilian University, Munich, Germany), and Prof. ErikRosenthal (University of New Haven, USA) for accepting the invitation to ad-dress the conference.

Three very good tutorials were part of TABLEAUX 2005: Instance-based

Methods (P. Baumgartner and G. Stenz), Analytic Systems and Dialogue Games

(C. Fermuller), and A Tutorial on Agda (M. Benke). Short descriptions of thesetutorials are included in this volume. I would like to express my thanks to thetutorial presenters for their contribution.

It was a team effort that made the conference so successful. I am truly gratefulto the Steering Committee members for their support and to Gernot Stenz for hisefficient work as Publicity Chair. And I particularly thank the local organizersfor their hard work and help in making the conference a success: Gerd Beuster,Sibille Burkhardt, Ruth Gotten, Vladimir Klebanov, Thomas Kleemann, JanMurray, Oliver Obst, Alex Sinner, Christoph Wernhard, and Doris Wertz.

September 2005 Bernhard Beckert

II

Program and Conference Chair

Bernhard Beckert University of Koblenz-Landau, Germany

Program Committee

Peter Baumgartner MPI Saarbrucken, GermanyMarta Cialdea Mayer University Roma Tre, ItalyRoy Dyckhoff University of St Andrews, ScotlandChristian Fermuller Vienna University of Technology, AustriaUlrich Furbach University of Koblenz-Landau, GermanyDidier Galmiche LORIA, University Henri Poincare, FranceMartin Giese RICAM, Austrian Acad. of Sci., Linz, AustriaRajeev Gore Australian Nat. Univ., Canberra, Australia

Jean Goubault-Larrecq Ecole Normale Superieure de Cachan, FranceReiner Hahnle Chalmers University, Gothenburg, SwedenUllrich Hustadt University of Liverpool, UKChristoph Kreitz University of Potsdam, GermanyReinhold Letz Munich University of Technology, GermanyCarsten Lutz Dresden University of Technology, GermanyMaarten Marx University of Amsterdam, The NetherlandsUgo Moscato University of Milano-Bicocca, ItalyNeil V. Murray University at Albany – SUNY, USAIlkka Niemela Helsinki University of Technology, FinlandNicola Olivetti University of Torino, ItalyLawrence Paulson University of Cambridge, UKDavid A. Plaisted University of North Carolina, USAPeter H. Schmitt University of Karlsruhe, GermanyViorica Sofronie-Stokkermans MPI Saarbrucken, GermanyArild Waaler University of Oslo, NorwayCalogero G. Zarba LORIA and INRIA-Lorraine, France / Univer-

sity of New Mexico, USA

III

Additional Referees

Pietro AbateWolfgang AhrendtAlessandro AvelloneArnon AvronMatthias BaazMathieu BaudetMaria Paola BonacinaClaudio CastelliniSerenella CerritoHans de NivelleStephane DemriMauro FerrariCamillo FiorentiniGuido Fiorino

Lilia GeorgievaLaura GiordanoMichael HansenKeijo HeljankoIan HorrocksHerman Ruge JervellTommi JunttilaYevgeny KazakovThomas KleemannLars KristiansenMartin LangeDominique

Larchey-WendlingPatrick MaierDaniel Mery

George MetcalfeClaudia NalonAndreas NonnengartMario OrnaghiVincent RischLuca RoversiGernot SalzerUlrike SattlerNiklas SorenssonGernot StenzCharles StewartChristoph WernhardPaul WongHantao Zhang

Steering Committee

Neil V. Murray University at Albany – SUNY, USA(President)

Jean Goubault-Larrecq Ecole Normale Suprieure de Cachan, France(Vice-President)

Bernhard Beckert University of Koblenz-Landau, GermanyPeter Baumgartner MPI Saarbrucken, GermanyRoy Dyckhoff University of St Andrews, ScotlandDidier Galmiche LORIA, University Henri Poincare, FranceReiner Hahnle Chalmers University, Gothenburg, Sweden

Organization

TABLEAUX 2005 was organized by the Artificial Intelligence Group at theInstitute for Computer Science of the University of Koblenz-Landau.

Sponsoring Institutions

German Research Foundation (DFG)University of Koblenz-LandauCity of KoblenzGovernment of Rhineland-PalatineGriesson - de Beukelaer GmbH

IV

Previous Meetings

1992 Lautenbach, Germany1993 Marseille, France1994 Abingdon, UK1995 St. Goar, Germany1996 Terrasini, Italy1997 Pont-a-Mousson, France1998 Oisterwijk, The Netherlands

1999 Saratoga Springs, USA2000 St Andrews, Scotland2001 Siena, Italy (part of IJCAR)2002 Copenhagen, Denmark2003 Rome, Italy2004 Cork, Ireland (part of IJCAR)

Table of Contents

Position Papers

A Prolog Tool for Relational Translation of Modal Logics: A Front-endfor Relational Proof Systems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1Andrea Formisano, Eugenio G. Omodeo, Ewa Or lowska

A Tableaux Calculus for KLM Preferential and Cumulative Logics . . . . . . 11Laura Giordano, Valentina Gliozzi, Nicola Olivetti, Gian Luca Pozzato

Tableau-like Axiomatization for Propositional Linear Temporal Logic . . . 27Nikolay V. Shilov

Tutorial Descriptions

Instance Based Methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41Peter Baumgartner, Gernot Stenz

Analytic Systems and Dialogue Games . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43Christian G. Fermuller

Tutorial on Agda . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53Marcin Benke

Author Index . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

A Prolog Tool for Relational Translation of

Modal Logics:

A Front-end for Relational Proof Systems?

Andrea Formisano1, Eugenio G. Omodeo2, and Ewa Or lowska3

1 Universita di L’Aquila, Italy; [email protected] Universita di Trieste, Italy; [email protected]

3 National Institute of Telecommunications, Warsaw, Poland; [email protected]

Introduction

Common approaches to the automation of modal inferences usually exploit ad

hoc, direct inference methods (cf., e.g., [20, 27]). An alternative approach, dis-cussed in the ongoing and aimed at developing a uniform relational platform formodal reasoning, is intended to benefit from relational renderings of non-classicallogics (cf. [23] among others).

The envisaged framework covers a full-fledged inferential apparatus, wherethe inferential activity is viewed as consisting of two phases. First, a translationphase carries a (propositional) modal formalization ϕ of a problem into its rela-tional counterpart. Then, within the relational context, a deductive method isexploited to seek for a proof of the translated formula ϕ.

There are several kinds of proof systems for relational reasoning: tableaux [14],Gentzen-style systems [28, 19], systems a la Rasiowa-Sikorski [22, 25, 4], displaycalculus [13], and of course equational proof systems based on relation alge-bras [9, 10]. The system we have in mind, should be seen as providing a conve-nient input for any of those proof systems. Specifically, the input for a tableaux-based system, a Gentzen system, or a Rasiowa-Sikorski system will be an ex-pression of the form x t(ϕ) y, where x and y stand for individual variables andt(ϕ) for a relational term translating the given formula ϕ, obtainable e.g. bymeans of a system which we have implemented in Prolog along lines that will bediscussed below. On the other hand, our input for an equational proof systemwill be an equation t(ϕ) = U , where U denotes the top element of a relationalgebra.

This paper mainly focuses on the translation phase: we describe a prototyp-ical, Prolog-based implementation of a tool, named transIt, able to uniformlycarry out translations from various modal logics to the relational formalism [29].

? Research partially funded by INTAS project Algebraic and deduction methods in non-classical logic

and their applications to Computer Science and by the European Concerted Research Action COSTAction-274, TARSKI: Theory and Applications of Relational Structures as Knowledge Instruments.

2 Andrea Formisano, Eugenio G. Omodeo, and Ewa Or lowska

We verified that this approach offers a high degree of uniformity: transIt

is able to treat varied modal logics by the very same machinery. Moreover,extensions to further classes of logics can easily be obtained by conservativelyadding their declarative Prolog specifications.

Notice that the adoption of a declarative programming approach allows usto develop the system in an incremental way and ensures high modularity andextensibility of the application. As well as further source languages can be added,the system can also be easily extended to encompass other target languages, soas to “drive” different (relational) proof systems. We exemplify this capabilityby extending transIt in order to use it as front-end for two deductive frameworkfor relation algebras which are rather different in nature (Section 4). The firstone consists in a minimal implementation of a proof-assistant (with some form ofautomated capabilities) based on Rasiowa-Sikorski rewriting rules [24]. Actually,the proof-assistant has been easily integrated in transIt by means of a commongraphical user interface. As a second approach to relational reasoning, we showhow transIt can be used as front-end for a first-order theorem-prover which isexploited as relational inference engine in the spirit of [9, 10].

1 Source and target languages

The main target languages which our translation supports are:

– the algebra of binary relations;– the binary first-order predicate calculus with 3-variables, namely L3 [29].

In the first case, given a formula ϕ the system produces a relational term t(ϕ)belonging to an algebraic language encompassing the usual constructs of Booleanalgebra plus further operators specific to the realm of relations. To be morespecific, following the work of Alfred Tarski [29], let us recall the basic notionson such formalism. The intended universe of discourse is a collection < of binaryrelations over a non-null domain U . We assume that the top relation

⋃<, and

the diagonal relation, consisting of all pairs 〈u, u〉 with u in U , belong to thisuniverse, which is also closed under the intersection (·), union (∪), complement

( ), composition (;), and conversion ( ^) operations. Within such a system, twoprimitive constants U and I designate the top and the diagonal relation, whilethe operations are interpreted as one expects (here, for any relational expressionR we are indicating by R= the relation over U designated by R), for instance:

– P^ designates the relation consisting of all pairs 〈v, u〉 with 〈u, v〉 in P =;– P ;Q designates the relation consisting of all pairs 〈u, w〉 such that there is at

least one v for which 〈u, v〉 and 〈v, w〉 belong to P = and to Q=, respectively;– P ·Q designates the relation consisting of all pairs 〈u, v〉 which simultaneously

belong to P= and to Q=;

A Prolog Tool for Relational Translation of Modal Logics 3

and similarly for the other constructs.Designations for further constants, operations over relations, or equations of

a special kind, can be introduced through definitions, e.g. as follows:

Z =Def U, D =Def I,

P−Q =Def P ·Q, P+Q =Def (Q∪P )−(Q·P ),PvQ ↔Def P−Q=Z.

As regards the binary first-order predicate calculus with 3-variables L3, thetranslation is obtained by first performing the translation into the algebra ofrelations, and then exploiting first-order characterizations of the relational oper-ators. Clearly, in order to limit the overall number of distinct first-order variablesto three, in doing the latter transformation we must rely on a suitable variablerecycling mechanism.

It should be noted that a first-order sentence is logically equivalent to asentence of L3 if and only if is expressible in the algebra of relations. This isbecause L3 is equipollent to the arithmetic of binary relations [29]. On the otherhand, in general, this is not the case if we consider sentences of the first-orderpredicate calculus. Actually, it is known (cf. [29, 18]) that the collection of allfirst-order sentences expressible with 3 variables (end hence having a relationalrendering) is undecidable. As a consequence, the translation from first-orderpredicate calculus into the algebra of relations is not always possible and it hasto be achieved (if possible) by exploiting conservative techniques. Therefore, theProlog translator may fail in translating a sentence. In spite of that, in anycase, the translation process ends. Notice that the translation process could beimproved by conservatively applying refinements of the translation technique(cf. for instance, [2]).

Similar enhancement can be applied in order to build into the tool furthertarget languages. One could easily achieve this goal by simply describing suchlanguages in terms of suitable rewriting rules.

Let us now briefly illustrate most of the source languages currently acceptedby the translator. The translation of each of them is actually based on specifictransformation rules. Besides propositional and predicative calculus, the follow-ing propositional modal logics can be treated:

Mono-modal logics. This is the basic translation of (propositional) modalformulas into relational terms originated in [22]. The source language in-volves usual propositional connectives together with necessity and possibilityoperators (here ψ, χ denote propositional sentences):

– t(pi) =Def p′

i; U , where p′

iis a relational variable uniquely corresponding

to each propositional variable pi;– t(¬ψ) =Def t(ψ);


– t(ψ & χ) =Def t(ψ) · t(χ);– t(♦ ψ) = Def r ; t(ψ), where r is a constant relation designating the

accessibility relation between possible worlds;And similarly for the other connectives.

Lattice-based modal logics. These logics, along with their corresponding re-lational renderings, are described in [26, 6, 17]. The Prolog translator canhandle the modal constructs of

- lattice-based modal logics with possibility operators;- lattice-based modal logics with necessity operators;- lattice-based modal logics with sufficiency operators.

Logics of knowledge and information. These modal logics come from [3]:- Logic with knowledge operator K, subject to the following translation

rule: t(Kϕ) =Def r; t(ϕ) ∪ r; t(ϕ).- Logic of non-deterministic information (NIL) [3, Sect. 7.2]. A multi-modal

logic with three modalities, representing the relations of inclusion andsimilarity proper of an information system.

- Information logic (IL) [3, Sect. 7.3]. A modal logic with three modal oper-ators corresponding to the relations of indiscernibility, forward inclusion,and similarity of an information system.

Intuitionistic logic. The translation of intuitionistic logic is based on thefollowing rules:

t(ψ→ χ) =Def 6; (t(ψ) · t(χ)) t(ψ & χ) =Def t(ψ) · t(χ)

t(¬ψ) =Def 6; t(ψ) t(ψ ∨ χ) =Def t(ψ) ∪ t(χ)

where 6 is a reflexive and transitive relation.Multi-modal logic. These logics correspond to multi-modal frames consisting

of a relational system (W,Rel) where Rel is a family of accessibility relations(enjoying closure properties with respect to relational constructs). Modalitiesare then of the form [R] and 〈R〉, where R is any relational term of Rel

(cf. [23]).Other modal logics. Other modal logics currently accepted by the translator

involve: logics with specification operators [15, 21], logics with Humberstoneoperators [16], logics with sufficiency operators [12, 5].

The system is currently being extended so as it can treat further logics, such astemporal logics (e.g., CTL).

2 The translation process

The translator takes as input a formula of a specific source language (see Sec-tion 1) and performs a sequence of rewriting transformations. Here is the se-quence of phases which usually form the translation (some of them being skippedin specific cases, for instance double-negation removal in intuitionistic logic):


Lexical and syntactical analyses. Depending on the specific language, thisphase accepts a formula only if its constructs belong to the language andthe formula is well-formed (i.e., syntactically correct). The syntax-directedtranslation implemented through this stage is described by an attributed def-inite clause grammar. Hence, any extension to further logics can be achievedby simply adding a suitable set of grammar rules which characterize the(new) well-formed formulas. The outcome of this stage is an intermediaterepresentation of the abstract syntax tree (AST) of the input formula.

Generation of an internal representation. By means of a rewriting pro-cess which acts in a bottom-up recursive fashion, the outcome of the preced-ing phase is turned into an internal representation of the AST, independentof the source language.

Reduction to primitive constructs. In this phase the formula is rewrittenin terms of a restricted set of constructs and connectives, to be regarded asbeing “primitive”. For instance, biimplication ↔ is rewritten as a conjunctionof two implications, and so on. Notice that some of the rewritings must beinhibited at times, insofar as unsound with respect to the specific logic athand. The aim of this transformation is to simplify the next phase.

Propositional simplifications. Through this phase the internal representa-tion of the formula is simplified by applying a number of propositional simpli-fications to it, mainly aimed at reducing the size of the formula (for instance,elimination of tautological sub-formulas and of double negations).

Relational translation. This is the main step of the translation process: theinternal representation of the given formula is translated into the calculus ofbinary relations. The kind of rewriting rules employed may depend on thesource language of the input formula (see Section 1). The outcome of thisphase is a relational term.

Relational simplifications. The overall translation process ends with a se-ries of relational simplifications applied to the relational term produced bythe preceding step. The simplest among these rewritings take care of theidempotency, absorption or involution properties of (some of) the relationalconstructs. The process can easily be extended to perform more complexsimplification.

Further phases could be added, for instance in order to apply semanticaltransformations to the relational term, possibly with respect to a set of ax-iomatic assumptions characterizing a particular class of relational structures asconstituting the target framework.

3 Input and outputs formats

When rawly used, our Prolog-based translation tool system reads a pure-textinput typed in by the user. The output is then written, also in pure-text format,


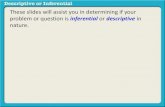
Fig. 1. Input dialog for formulas

to the standard output stream (usually, the screen). This kind of interaction is,however, quite unsatisfactory, because the ASCII character set is rather poor.In order to overcome this disadvantage and ease the input/output of complexformulas and expressions, a user-friendly interface has been developed. Such agraphical interface allows the user to type in formulas using graphical LATEX-generated symbols. In doing this, we exploited the useful integration facilitiesoffered by SICStus Prolog [31] with respect to other programming languages.Figure 1 displays a generic input dialog achieved with the Tcl/Tk toolkit [30].

The system also provides the possibility of processing a text file, as well asto generate a text file as output. Through this feature it is possible to produceinput files for different deduction tools (see Section 4).

Let us briefly illustrate the use of the graphical interface with a simple exam-ple. Consider the multi-modal formula [R ∪Q] < Q > p → q. This formula canbe easily input to the translator as shown in Figure 1. The relational equationobtained can also be displayed graphically, as in Figure 2.

4 Driving a deductive tool

As mentioned the main purpose of transIt consists in providing an extensiblefront-end for (relational) deductive systems.


Fig. 2. Output of a translation process

To exemplify this capability, in what follows we report on two extensions oftransIt, designed in order to use it as front-end for two deductive framework forrelation algebras which are rather different in nature. The first one consists ina minimal implementation of a proof-assistant (with some form of automatedcapabilities) based on Rasiowa-Sikorski rewriting rules [24]. Such proof-assistantis accessible through transIt ’s graphical interface. Once the user obtained arelational rendering of a theorem, he can proceed trying to build a proof-tree ofthe relational translation. Figure 3 shows a simple example of derivation tree.The user interacts with the system by simply choosing a node of the tree inorder to apply one of the rewriting rules. The system takes care of verifyingapplicability of rules, performing the extension of the tree, and checking if, asa consequence of rule applications, any branch becomes closed. Some form of(semi-)automated reasoning capabilities are also implemented: it is possible toask the system to try, autonomously, to close all the branches of a (sub-)tree.

Fig. 3. Assisted development of a proof tree


Another viable approach to relational reasoning consists in using transIt asfront-end for a first-order theorem-prover, Otter, in this case. This is achievedby extending the translation process: a new set of rewriting rules is used toimplement automated generation of an input file to be fed to Otter. Once theinput file is available, Otter can be used as described in [9, 10] to search for aproof of the theorem within the relational framework. Clearly, the very sameapproach can be used with other theorem provers.

Currently, transIt can be downloaded from the site http://www.di.univaq.it/TARSKI/transIt/ and easily installed. It is developed under Linux, but wealso provide a porting for Windows XP.

5 Ongoing work

Most of the features described in the previous sections are steadily subject toameliorations and other are being designed. In particular, we are currently in-terested in:

– Enriching the collection of target languages, so to permit, for instance:

• Translations into the language of the theory of aggregates described in [7,1]. In this case, the result of the translation could be fed into a deductionsystem for theory-based reasoning [11].

• Output in terms of LATEX commands (for both input and output formu-las).

– Improving the translation process by enriching and refining the set of rewrit-ing rules which, at the moment, are largely realized through merely syntacti-cal rewriting rules. A goal would consist in enhancing the translation processby improving its capability of exploiting semantic properties of connectivesand constructs.

– Improving the user interface, by addition of more features and control on theinput/output, on the translation process, and on the proof-assistant.

– Exploring the possibilities offered by integration with/within other tools fortranslation and deduction.

– Exploitation, in the derivation process (both for the assisted and the au-tonomous cases), of specific rewriting rules, depending on the particular logicof the theorem being proved.

A further long-term activity regards the integration with visual-oriented toolsfor manipulation of relational formulas, (based, for instance, on graphical rep-resentation of relational expressions and on graph-rewriting techniques [8]).


Acknowledgments

Thanks are due to Marianna Nicolosi Asmundo and to Hui Wang for fruitfuldiscussions on the topics of this paper, as well as to the anonymous referees forhelpful comments.

References

1. J. F. A. K. van Benthem, G. D’Agostino, A. Montanari, and A. Policriti. Modal deduction insecond-order logic and set theory-I, J. Logic Comput., 7(2):251–265, 1997.

2. D. Cantone, A. Formisano, E. G. Omodeo, C. G. Zarba. Compiling dyadic first-order specificationsinto map algebra. Theoretical Computer Science, 293(2):447–475, 2003.

3. S. Demri, E. Or lowska. Incomplete Information: Structure, Inference, Complexity. Springer 2002.4. M. Frias and E. Or lowska. Equational reasoning in nonclassical logics. J. of Applied Non-Classical

Logics, 8(1-2):27–66, 1998.5. I. Duntsch and E. Or lowska. Beyond modalities: sufficiency and mixed algebras. In E. Or lowska

and A. Szalas eds., Relational Methods in Computer Science Applications. pp.277–299. Physica-Verlag, Heidelberg, 2000.

6. I. Duntsch, E. Or lowska, A. M. Radzikowska, and D. Vakarelov. Relational Representation The-orems for Some Lattice-Based Structures. JoRMiCS, 1:132–160, 2004.

7. A. Formisano, E. Omodeo, E. Or lowska, and A. Policriti. Uniform relational frameworks for modalinferences. In I. Duntsch and M. Winter eds., Proc. of the 8th Int. Conf. on Relational Methodsin Computer Science (RelMiCS 8), 2005.

8. A. Formisano, E. Omodeo, M. Simeoni, A graphical approach to relational reasoning. Electr.

Notes Theor. Comput. Sci., 44(3), Elsevier, 2001.9. A. Formisano, E. G. Omodeo, M. Temperini. Instructing Equational Set-Reasoning with Otter.

Proc. of IJCAR 2001. LNCS 2083, pp.152–167, 2001.10. A. Formisano, E. G. Omodeo, M. Temperini. Layered map reasoning: An experimental approach

put to trial on sets. Electr. Notes Theor. Comput. Sci., 48, Elsevier, 2001.11. A. Formisano and A. Policriti. T -Resolution: Refinements and Model Elimination. J. Autom.

Reasoning, 22(4):433–483, Kluwer, 1999.12. V. Goranko. Modal definability in enriched languages. Notre Dame Journal of Formal Logic,

31:81–105, 1990.13. R. Gore. Cut-free display calculi for relation algebras. In D. van Dalen and M. Bezem eds., CSL96:

Selected Papers of the Annual Conference of the Association for Computer Science Logic, LNCS1258, pp.198–210. Springer, 1996.

14. M. C. B. Hennessy. A proof system for the first order relational calculus. J. of Computer and

System Sciences, 20:96–110, 1980.15. C. A. R. Hoare and H. Jifeng. The weakest prespecification. Part I Fundamenta Informaticae,

IX:51–84; Part II ibidem IX:217-252, 1986.16. I. L. Humberstone. Inaccessible worlds. Notre Dame Journal of Formal Logic, 24:346–352, 1983.17. J. Jarvinen and E. Or lowska. Relational correspondences for lattices with operators. In I. Duntsch

and M. Winter eds., Proc. of the 8th Int. Conf. on Relational Methods in Computer Science(RelMiCS 8), pp.111–118, 2005.

18. M. K. Kwatinetz. Problems of expressibility in finite languages. PhD thesis, University of Cali-fornia, Berkeley, 1981.

19. R. Maddux. A sequent calculus for relation algebras. Annals of Pure and Applied Logic, 25:73–101, 1983.

20. H. J. Ohlbach, A. Nonnengart, M. de Rijke, and D. Gabbay. Encoding Two-Valued NonclassicalLogics in Classical Logic, In Handbook of Automated Reasoning, vol. II, pp.1403–1486, Elsevier,2001.

21. E. Or lowska. Proof system for weakest prespecification. Information Processing Letters, 27:309–313, 1988.


22. E. Or lowska. Relational interpretation of modal logics, In H. Andreka, D. Monk, and I. Nemetieds., Algebraic Logic. Colloquia Mathematica Societatis Janos Bolyai, vol. 54, pp.443–471, NorthHolland, 1988.

23. E. Or lowska. Relational semantics for nonclassical logics: formulas are relations, PhilosophicalLogic in Poland (J. Wolenski, ed.), pp.167–186. Kluwer, 1994.

24. E. Or lowska. Relational proof systems for modal logics, In H. Wansing ed., Proof theory of modal

logic, Applied logic series, vol.2, pp.55–78. Kluwer, 1996.25. E. Or lowska. Relational formalization of nonclassical logics. In C. Brink, W. Kahl, and G. Schmidt

eds., Relational Methods in Computer Science, pp.90-105. Springer, Wien, New York.26. E. Or lowska and D. Vakarelov. Lattice-based modal algebras and modal logics. In P. Hajek,

L. Valdes, D. Westerstahl eds., Proc. of the 12th Int. Congress of Logic, Methodology and Phi-losophy of Science, Oviedo, Spain, 2003, Elsevier.

27. R. Schmidt and U. Hustadt. Mechanized reasoning and model generation for extended modallogics. In H. de Swart, E. Or lowska, G. Schmidt, and M. Roubens, eds., Theory and Applications

of Relational Structures as Knowledge Instruments, Springer, LNCS 2929, pp.38–67, 2003.28. W. Schoenfeld. Upper bounds for a proof search in a sequent calculus for relational equations.

Zeitschrift fuer Mathematische Logic und Grundlagen der Mathematik 28:239–246, 1982.29. A. Tarski and S. Givant. A formalization of Set Theory without variables, Colloquium Publica-

tions, vol. 41, American Mathematical Society, 1987.30. Web resources for the Tcl/Tk toolkit: http://tcl.sourceforge.net.31. Web reference for SICStus Prolog: http://www.sics.se/sicstus.

A Tableaux Calculus for KLM Preferential and

Cumulative Logics

Laura Giordano∗, Valentina Gliozzi∗∗, Nicola Olivetti∗∗, Gian Luca Pozzato∗∗

∗Dipartimento di Informatica - Universita del Piemonte Orientale A. Avogadro - Corso Borsalino 54- 15100 Alessandria, Italy - E-mail: [email protected]

∗∗Dipartimento di Informatica - Universita degli Studi di Torino - Corso Svizzera 185 - 10149Torino, Italy - E-mail: {gliozzi,olivetti,pozzato}@di.unito.it

Abstract. We present tableaux calculi for some logics of default reasoning, as definedby Kraus, Lehmann and Magidor. We give a tableaux proof procedure for preferentiallogic P and for loop-cumulative logic CL. Our calculi are obtained by introducingsuitable modalities to interpret conditional assertions. Moreover, they give a decisionprocedure for the respective logics and can be used to establish their complexity.

1 Introduction

In the early 90’ [9] Kraus, Lehmann and Magidor (from now on KLM) proposeda formalization of non-monotonic reasoning that was early recognized as a land-mark. Their work stemmed from by two sources: the theory of nonmonotonicconsequence relations initiated by Gabbay [6] and the preferential semanticsproposed by Shoham [11] as a generalization of Circumscription. Their workslead to a classification of nonmonotonic consequence relations, determining ahierarchy of stronger and stronger systems.

According to the KLM framework, defeasible knowledge is represented bya (finite) set of nonmonotonic conditionals or assertions of the form A |∼ B

whose reading is normally (or typically) the A’s are B’s. The operator ”|∼”is nonmonotonic, in the sense that A |∼ B does not imply A ∧ C |∼ B. Forinstance K may contain the following set of conditionals: adult |∼ work, adult |∼

taxpayer, student |∼ adult, student |∼ ¬work, student |∼ ¬taxpayer, retired |∼

adult, retired |∼ ¬work, whose meaning is that adults typically work, adultstypically pay taxes, students are typically adults, but they typically do notwork, nor they do pay taxes, and so on. Observe that if |∼ were interpretedas classical (or intuitionistic) implication, we simply would get student |∼ ⊥,retired |∼ ⊥, i.e. typically there are not students, nor retired people, therebyobtaining a trivial knowledge base. One can derive new conditional assertionsfrom the knowledge base by means of a set of inference rules.

In KLM framework, the set of adopted inference rules defines some funda-mental types of inference systems, namely, from the weakest to the strongest:Cumulative (C) , Loop-Cumulative (CL), Preferential (P) and Rational logic(R). All these systems allow one to infer new assertions from K without incur-ring in the trivialising conclusions of classical logic: regarding our example, in

12 Laura Giordano, Valentina Gliozzi, Nicola Olivetti, Gian Luca Pozzato

none of them, one can infer student |∼ work or retired |∼ work. In cumulativelogics (both C and CL) one can infer adult ∧ student |∼ ¬work (giving prefer-ence to more specific information), in Preferential logic P one can also infer thatadult |∼ ¬retired (i.e. typical adults are not retired). In the rational case R, ifone further knows that adult 6|∼ ¬married (i.e. it is not the case the adults aretypically unmarried), one can also infer that adult ∧married |∼ work.

From a semantic point of view, to the each logic (C, CL, P, R) correspondsone kind of models, namely, possible-world structures equipped with a prefer-ence relation among worlds or states. More precisely, for P we have models witha preference relation (an irreflexive and transitive relation) on worlds. For thestronger R the preference relation is further assumed to be modular. For theweaker logic CL, the preference relation is defined on states, where a state canbe identified, intuitively, with a set of worlds. In the weakest case of C, thepreference relation is on states, as for CL, but it is no longer assumed to betransitive. In all cases, the meaning of a conditional assertion A |∼ B is that B

holds in the most preferred worlds/states where A holds.In KLM framework the operator ”|∼” is considered as a meta-language oper-

ator, rather than as a connective in the object language. However, it has beenreadily observed that KLM systems P and R coincide to a large extent withthe flat (i.e. unnested) fragments of well-known conditional logics, once we in-terpret the operator ”|∼” as a binary connective [3], [2], [8]. The connectionswith conditional and modal logic have been studied further in two directions. Arecent result by Halpern and Friedman [4] has shown that preferential and ratio-nal logic are quite natural and general systems: surprisingly enough, the axiomsystem of preferential (likewise of rational logic) is complete with respect to awide spectrum of semantics: from ranked models, to parametrized probabilisticstructures, ε-semantics and possibilistic structures. The result of Halpern andFriedman can be explained by the fact that all these structures are examplesof plausibility structures (or plausibility ordered structures), and the truth inthem is captured by the axioms of preferential (or rational) logic. These results,and their extensions to the first order setting [5] are the source of a renewedtheoretical interest in KLM framework.

On the other hand, Lamarre and then Boutillier [2] have shown that pref-erential and rational logic (but not the weaker C and CL) could be translatedinto standard modal logics, although the proposed translation is not the mostnatural.

Even if KLM was born as an inferential approach to nonmonotonic reasoning,curiously enough, there has not been much investigation on deductive mecha-nisms for these logics. Lehmann has proved that deciding whether a conditionalis entailed by a set of positive conditionals is a CoNP problem in both the pref-erential and the rational case. Decidability of P and R can be also proved bymapping them into standard modal logics [2]. A tableaux proof procedure for

A Tableaux Calculus for KLM Preferential and Cumulative Logics 13

cumulative logic has been given in [1]. To the best of our knowledge, for CL nodecision procedure was known before the present work.

In this work we begin our investigation of tableaux procedures for KLM log-ics, by considering the cases of P and CL. The investigation of tableaux calculifor the weakest C and the strongest R is left for future work. Our approach isbased on a sort of run-rime translation of P conditional assertions into modallogic G. The idea is simply to interpret the preference relation as an accessibilityrelation: a conditional A |∼ B holds in a model if B is true in all A-worlds w

that are minimal. An A-world is minimal if all smaller worlds are not A-worlds.The relation with G is motivated by the fact that we assume, following KLM,the so-called smoothness condition, which is related to the limit assumption.This condition ensures indeed that A-minimal worlds exist, by preventing aninfinitely descending chain of worlds. This condition is therefore ensured by thefinite-chain condition on the accessibility relation (as in modal logic G). There-fore, our interpretation of conditionals is different from the one proposed byBoutilier, who rejects the smoothness condition, and as a consequence, gives amore complicate interpretation of P into modal logic S4. Moreover, we do notgive a formal translation of P in G, we appeal to the correspondence as far asit is needed to derive the tableaux rules for P.

We are able to extend our approach to the case of CL by using a secondmodality which takes care of states. More precisely, we show that we can mapCL-models into P-models with an additional modality; this fact seems to haveremained unnoticed and might be of independent interest. In both cases, P andCL, we can define a decision procedure and obtain also a complexity bound forthese logics, namely that they are both CoNP. In case of CL this bound is new,at the best of our knowledge.

The plan of the paper is as follows: in section 2, we recall preferential logic P.In section 3, we give a simple tableaux calculus for P, and we prove its sound-ness and completeness. In section 4 we improve the calculus to obtain a decisionprocedure for P and we prove that it is CoNP. In section 5, we give a similarcalculus for logic CL, obtaining a decision procedure and a CoNP complexitybound for it. In section 6, we discuss some related works and we suggest somefuture developments.

2 Preferential Logic P

The language of KLM logics consists just of assertions A |∼ B. We consider aricher language allowing boolean combinations of assertions and propositionalformulas.

The language L of P is defined from a set of propositional variables ATM ,the boolean connectives and the conditional operator |∼. The formulas of L aredefined as follows: if A is a propositional formula, A ∈ L; if A and B are


propositional formulas, A |∼ B ∈ L; if A is a boolean combination of formulas ofL, A ∈ L.

The axiomatization of P consists of all axioms and rules of propositionalcalculus together with the following axioms and rules:

• REF. A |∼ A (reflexivity)• LLE. If |= A↔ B, then from A |∼ C infer B |∼ C (left logical equivalence)• RW. If |= A→ B, then from C |∼ A infer C |∼ B (right weakening)• CM. ((A |∼ B) ∧ (A |∼ C))→ (A ∧ B |∼ C) (cautious monotonicity)• AND. ((A |∼ B) ∧ (A |∼ C))→ (A |∼ B ∧ C)• OR. ((A |∼ C) ∧ (B |∼ C))→ (A ∨B |∼ C)

The semantics of P is defined by considering possible world structures witha preference relation (a strict partial order) w < w

′whose meaning is that w

is preferred to w′. We have that A |∼ B holds in a model M if B holds in all

minimal worlds with respect to the relation < where A holds. This definitionmakes sense provided minimal worlds for A exist whenever there are A-worlds.This is ensured by the smoothness condition in the next definition.

Definition 1 (Semantics of P). A model is a triple M = 〈W, <, V 〉 where:W is a non-empty set of items called worlds; < is an irreflexive and transitiverelation on W; V is a function V : W 7−→ pow(ATM), which assigns to everyworld w the set of atoms holding in that world. We define the truth conditions(M, w |= A) as follows:

• M, w |= A for the boolean cases is defined in the obvious way;• Let A be a propositional formula; we define Min<(A) = {w | M, w |= A

and ∀w′< w M, w

′6|= A};

• M, w |= A |∼ B if for all w′∈Min<(A), then M, w

′|= B.

We assume that the relation < satisfies the following condition, called smooth-ness: if M, x |= A then x ∈Min<(A) or ∃y ∈Min<(A) such that y < x.We say that a formula A is valid in a model M, denoted with M |= A, if itrespects the truth conditions in all worlds of the model, i.e.M, w |= A for everyw ∈ W. A formula is valid if it is valid in every modelM.

Given a modelM, we denote by [A] the set of worlds w such thatM, w |= A.We also introduce in L a modality �, whose intuitive meaning is as follows:

�A holds in a world w if A holds in all the worlds w′such that w

′< w:

Definition 2 (Truth condition of modality �). We define the truth condi-tion of a boxed formula as follows:

M, w |= �A iff for every w′∈ W if w

′< w then M, w

′|= A

Observe that for any formula A we have that w ∈ Min<(A) iff M, w |=A∧�¬A. It is easy to see that � has the properties of the modal system G: theaccessibility relation (i.e. Rxy iff y < x) is transitive and does not have infiniteascending chains.


3 The Tableaux Calculus for Preferential Logic P

In this section we present a tableaux calculus for P called T P. To save space,we only give propositional rules for ¬ and ∧.

Definition 3 (The calculus T P). The rules of the calculus manipulates setsof formulas G. In the rules we write G, A to denote G ∧ A. Moreover, given G

we define the following:

– G� = {�A | �A ∈ G} − G�↓= {A | �A ∈ G}

– G|∼+

= {A |∼ B | A |∼ B ∈ G} − G|∼−

= {¬(A |∼ B) | ¬(A |∼ B) ∈ G}

– G|∼± = G|∼+

∪G|∼−

The tableaux rules are given in Figure 1.

(AX) G, A,¬A (¬)G,¬¬A

G, A

(|∼+)G, A |∼ B

G,¬A, A |∼ B G,¬�¬A, A |∼ B G, B, A |∼ B

(|∼−)G,¬(A |∼ B)

A, �¬A,¬B, G|∼±

(�−)G,¬�A

G�

, G�↓

, G|∼±

,¬A, �A

(∧+)G, A ∧ B

G, A, B

(∧−)G,¬(A ∧ B)

G,¬A G,¬B

Fig. 1. Tableaux system T P.

(A |∼ C) ∧ ¬(A ∧ C |∼ C)(∧+)

A |∼ C,¬(A ∧ C |∼ C)(|∼−)

A |∼ C, A ∧ C, �¬(A ∧ C),¬C

(∧+)A |∼ C, A, C,¬C, �¬(A ∧ C)

×

Fig. 2. A derivation of (A |∼ C) ∧ ¬(A ∧ C |∼ C) in T P.

The system is sound and complete with respect to the semantics.

Theorem 1 (Soundness of T P). The system T P is sound with respect to thesemantics, i.e. if there is a closed tableaux for a set G, then G is unsatisfiable.


To prove the completeness of T P we have to show that if A is unsatisfiable,then there is a closed tableaux starting with A. We prove the contrapositive,that is: if there is no closed tableaux for A, then there is a model satisfyingA. To build this model, the idea is to select sets with certain properties frompossibly different open tableaux for A. This proof is inspired by [?].First of all, we distinguish static and dynamic rules. (|∼−) and (�−) are calleddynamic, since their conclusion represents another world with respect to thepremise; the other rules are called static, since the world represented by premiseand conclusion(s) is the same. Moreover, we have to introduce the saturation ofa set of formulas G. Given a set of formulas G, we say that it is saturated if allthe static rules have been applied.

Definition 4 (Saturated sets). A set of formulas G is saturated with respectto the static rules if the following conditions hold:

– if A ∧B ∈ G then A, B ∈ G;– if ¬(A ∧B) ∈ G then ¬A ∈ G or ¬B ∈ G;– if ¬¬A ∈ G then A ∈ G;– if A |∼ B ∈ G then ¬A ∈ G or ¬�¬A ∈ G or B ∈ G.

Lemma 1. Given a finite set of formulas G, there is a finite and saturated setG

′⊇ G. Moreover, if G is consistent, then G

′is consistent.

By Lemma 1, we can think of having a function which, given a consistentset G, returns one fixed consistent saturated set, denoted by SAT(G). Moreover,we denote by APPLY(G, F ) the result of applying to G the rule for the principalconnective in F . In case the rule for F has more conclusions (the case of a branch-ing), we suppose that the function APPLY chooses one consistent conclusion inan arbitrary but fixed manner.

Theorem 2 (Completeness of T P). T P is complete with respect to the se-mantics.

Proof. As mentioned above, we assume that no tableaux for G0 is closed, thenwe construct a model for G0. We build X, the set of worlds of the model, asfollows:

1. initialize X = {SAT(G0)};2. choose G ∈ X;3. for each formula ¬(A |∼ B) ∈ G, be G¬(A|∼B) =SAT(APPLY(G,¬(A |∼ B))). If

G¬(A|∼B) 6∈ X, then X = X ∪G¬(A|∼B);4. for each formula ¬�A ∈ G, be G¬�A =SAT(APPLY(G,¬�A));

– add the relation G¬�A < G;– if G¬�A 6∈ X, then X = X ∪G¬�A.

5. repeat from 2 until all elements in X have been considered.


This procedure terminates, since the number of possible sets of formulas thatcan be obtained by applying T P’s rules to an initial finite set G is finite. Weconstruct the modelM = 〈X, <X , V 〉 for G as follows:

• <X is the transitive closure of the relation <;• V (G) = {P | P ∈ G}

In order to show thatM is a preferential model for G, we prove the followingfacts:

Fact 1 The relation <X is acyclic.

Proof. If there were a loop we would have the following situation: there are G1

and G3 in X, G3 <X G1, and G1 is obtained again from G3 by applying step4 (i.e. G1 <X G3). This situation, presented in Figure 3, will never happen.Indeed, since G3 <X G1, G3 has been generated by a sequence of applicationsof (�−), starting from an initial application of (�−) to some formula ¬�α inG1. By the (�−) rule, �α ∈ G3. If G1 were to be generated again from G3 byan application of (�−), then �α ∈ G1, which contradicts the fact that G1 isconsistent. ut

Fig. 3.

Fact 2 For all formulas F and for all sets G ∈ X we have:

– if F ∈ G then M, G |= F ;– if ¬F ∈ G then M, G 6|= F .

Proof. By induction on the structure of F . If F is an atom P , thenM, G |= P bydefinition of V . If F is ¬P , then ¬P ∈ G implies that P 6∈ G as G is not closed;thus, M 6|= P (by definition of V ). For the inductive step we only consider thecase of (¬) |∼ and (¬)�:

– �A ∈ G. Then, for all Gi <X G we have A ∈ Gi since Gi has been generatedby a sequence of applications of (�−), and by definition of (�−). By inductivehypothesis M, Gi |= A, whence M, G |= �A.

– ¬�A ∈ G. By construction there is a G′ s.t. G′ <X G and {�A,¬A} ⊆ G′.By inductive hypothesis M, G′ |= ¬A. Thus, M, G 6|= �A.


– A |∼ B ∈ G: we have to show that M, G |= A |∼ B. Let H ∈ Min<X(A);

one can observe that (1)¬A ∈ H or (2)¬�¬A ∈ H or (3)B ∈ H, since H

is saturated. (1) cannot be, since by inductive hypothesis M, H |= A. If (2),by the construction ofM there exists a set H

′<X H such that A ∈ H

′. By

inductive hypothesis M, H′|= A, which contradicts H ∈Min<X (A). Thus it

must be (3)B ∈ H, so that by the inductive hypothesis M, H |= B.– ¬(A |∼ B) ∈ G: by construction of X, there exists G

′∈ X such that

A, �¬A,¬B ∈ G′. By inductive hypothesis we have that M, G

′|= A and

M, G′|= �¬A. It follows that G

′∈ Min<X

(A). Furthermore, always byinduction,M, G

′6|= B.

utBy the above Lemma the proof of the completeness of T P is over, since M

is a model for the initial set G0. ut

A relevant property of the calculus that will be useful to estimate the com-plexity of logic P is the so-called disjunction property of conditional formulas:

Proposition 1 (Disjunction property). If there is a closed tableaux for G,¬(A |∼

B),¬(C |∼ D), then there is a closed tableaux either for G,¬(A |∼ B) or forG,¬(C |∼ D).

The reason why this property holds is that the (|∼−) rule discards all theother formulas that could have been introduced by a previous application of thisrule.

4 Decision Procedure for P

In this section we analyze the calculus T P in order to obtain a decision procedurefor logic P. We also give explicit complexity bound for it.

First, we observe that the above calculus T P does not ensure a terminatingproof search; in fact, the (|∼+) rule can be applied without any control, andthis is a potential cause of the construction of infinite branches. The intuitionis as follows: one needs to apply the (|∼+) rule on A |∼ B only if any formulasintroduced by the rule (i.e. ¬A, ¬�¬A and B) is not already in the premise. Wealso need to reformulate the rules for the boolean connectives, in such a way thatthe formula to which the rule is applied is maintained in the conclusion. Thisreformulation is needed to avoid to reconsider a positive conditional A |∼ B oncethat its propositional subformulas (¬A and B) have been added to the currentset of formulas. Since these subformulas might be later decomposed, if we do notkeep them we would not be able to block the re-application of (|∼+) on A |∼ B.

The terminating calculus T PT is presented in Figure 4.The calculus T PT is sound and complete with respect to the semantics; we

briefly show the completeness, as the soundness is immediate.


(|∼+)G, A |∼ B

G,¬A, A |∼ B G,¬�¬A, A |∼ B G, B, A |∼ B

if G ∩ {¬A,¬�¬A, B} = ∅

(∧+)G, A ∧ B

if A 6∈ G

G, A ∧ B, A

(∧+)G, A ∧ B

if B 6∈ G

G, A ∧ B, B

(∧−)G,¬(A ∧ B)

if ¬A,¬B 6∈ G

G,¬(A ∧ B),¬A G,¬(A ∧ B),¬B

(¬)G,¬¬A

if A 6∈ G

G,¬¬A, A

Fig. 4. The calculus T PT. Omitted rules (�−) and (|∼−) are the same as in Figure 1.

Theorem 3 (Completeness of T PT). The calculus T PT is complete withrespect to the semantics.

Proof. We show that if G is derivable in T P (i.e. there exists a closed tableauxwith root G), then G is derivable in T PT. The prove is by induction on theheight of the derivation of G in T P. If G is an axiom, we are done; otherwise,consider the rule applied to G: if it is (�−) or (|∼−), then we can conclude sincethe two rules are identical in the two calculi. The same for an application of (|∼+);indeed, if (|∼+) is applied to G

′, A |∼ B, then we have to distinguish two cases:

(i) ¬A,¬�¬A, B 6∈ G′: in this case we can easily conclude by an application of

(|∼+) in T PT; (ii) ¬A ∈ G′or ¬�¬A ∈ G

′or B ∈ G

′: in this case, the (|∼+) rule

is not applicable, by the restriction given in T PT. However, we are analyzingthe case when, in T P, the (|∼+) rule has been applied on G

′, A |∼ B and one

of the three conclusions is the same as the set G′, A |∼ B, therefore this rule

application is useless and can be removed. By this fact, we can conclude theproof.

For the rules related to boolean connectives the proof is easy and left tothe reader. As an example, consider (∧+) applied to G

′, A ∧B and just observe

that if A, B 6∈ G′, then we obtain a proof in T PT by two applications of (∧+),

otherwise at least one of the conclusions of the rule is identical to the premise,therefore it is useless to add both subformulas. ut

In order to prove that T PT ensures a terminating proof search, we define acomplexity measure on a set of formulas G, denoted by m(G), which consists offour measures c1, c2, c3 and c4 in a lexicographic order. Before giving the formaldefinition, we need to define the following:

Definition 5 (Saturation multiset S of G). Given a set of formulas G, wedefine the saturation multiset S as follows:


S = {F ∈ G | (F = A ∧B and (A 6∈ G or B 6∈ G)) or(F = ¬(A ∧ B) and (¬A 6∈ G and ¬B 6∈ G)) or ((F = ¬¬A) and (A 6∈ G))}

Notice that S is a multiset; in particular, if F = A ∧ B and both A 6∈ G andB 6∈ G, then two instances of F = A ∧ B belong to S, whereas if A 6∈ G andB ∈ G, then only one instance of F = A ∧B belongs to S.

We write A |∼ B ∈+ G (resp. A |∼ B ∈− G) if A |∼ B occurs positively(resp. negatively) in G, where positive and negative occurrences are defined inthe standard way. We also denote with cp(F ) the complexity of a formula F .

Definition 6 (Lexicographic order). We define m(G) = 〈c1, c2, c3, c4〉 where:

• c1 =| {A |∼ B ∈− G} |;• c2 =| {A |∼ B ∈+ G | �¬A 6∈ G} |;• c3 =| {A |∼ B ∈+ G | {¬A,¬�¬A, B} ∩G = ∅} |;• c4 =

∑F∈S cp(F ).

We consider the lexicographic order given by m(G).

Intuitively, c2 represents the number of positive conditionals in G which canstill create a new world. The application of (�−) reduces c2: indeed, if (|∼+) isapplied to A |∼ B, this application introduces a branch containing ¬�¬A; whena new world is generated by an application of (�−) on ¬�¬A, it contains A and�¬A. If (|∼+) is applied to A |∼ B once again, then the conclusion where ¬�¬Ais introduced is closed, by the presence of �¬A in that branch. c4 represents thesaturation degree, i.e. the sum of the complexities of formulas to which one canstill apply propositional rules.

In order to prove that T PT ensures a terminating proof search we need thefollowing:

Lemma 2. Let G′be obtained by an application of a rule of T PT to a premise

G. Then, m(G′) < m(G).

Now we have all the elements to prove that T PT ensures a terminating proofsearch:

Theorem 4 (Termination of T PT). T PT ensures a terminating proof search.

We conclude this section with a complexity analysis of T PT, in order toprove that validity in P belongs to CoNP. First of all, notice that we couldtake advantage of the disjunction property (Proposition 1). By this property wecan reformulate the (|∼−) rule as follows:

G,¬(A |∼ B)(|∼−)

A, �A,¬B, G|∼+


This rule reduces the length of a branch at the price of making the proofsearch more non-deterministic. Moreover, observe that with this reformulationthe parameter c1 would no longer be needed.

We give a non-deterministic algorithm for testing validity in P that: (i) takesa set of formulas G as input; (ii) returns false iff G is satisfiable; (iii) generatesa branch starting with G of polynomial length and requiring only a polynomialnumber of guesses in the size of G. The algorithm is defined below; in bracketswe give the complexity of each operation, considering that n =| G |. Moreover,we assume that after each step from 1. to 4., a procedure CHECK, obviously ofpolynomial complexity, is invoked to verify if the current set of formulas is anaxiom and, in that case, the execution terminates returning true:

input G: set of formulas;output boolean;begin

1. G′←− guess one branch applying only propositional rules; (O(n))

2. G′←− guess one ¬(Aj |∼ Bj) ∈ G

′and apply (|∼−) on it; (O(n))

3. for each Ai |∼ Bi ∈ G′do

3.1. G′←− G

′∪ one of ¬Ai,¬�¬Ai and Bi; (O(1))

3.2. G′←− guess one branch applying only propositional rules; (O(n))

4. if ¬�¬A1, ...¬�¬Ak ∈ G′

4.1. G′←− guess one ¬�¬Ai and apply (�−) on it; (O(1))

4.2. repeat from 3.;5. if G

′is an axiom return true;

else return false;end

Observe that when the algorithm exit the cycle no rule is applicable to thecurrent set of formulas. Moreover, it can be shown that one can repeat the cyclebetween instructions 3. and 4. at most n times. Therefore, the complexity of thecycle is O(n2).

Theorem 5 (Complexity of P). Validity of preferential logic P is CoNP.

Proof. A is not valid in P iff the algorithm returns false. Since the algorithmis NP, non validity is NP; therefore, validity is CoNP. ut

5 Loop Cumulative Logic CL

In this section we develop a tableaux calculus for CL. First we define a mappingof KLM cumulative models to preferential models which are essentially obtainedby extending P-models with an additional accessibility relation R. Then, wedefine tableaux calculus T CL for CL and we show that the calculus T CL can


be turned into a terminating calculus thus providing a decision procedure forCL and a CoNP complexity bound for validity in CL.

Let us first recall the axiomatization of the system CL and the notion ofcumulative models as given by KLM in [9]. The axiomatization of the systemCL can be obtained by the axiomatixation of the system P by removing theaxiom OR and by adding the following infinite set of axioms LOOP:

(LOOP ) (A0 |∼ A1) ∧ (A1 |∼ A2)...(An−1 |∼ An) ∧ (An |∼ A0)→ (A0 |∼ An)

Notice that these axioms are derivable in P.

Definition 7 (Cumulative model (KLM)). A cumulative model is a tupleM = 〈S, l, <, V 〉, where S is a set, whose elements are called states; l : S 7→ 2U

is a function that labels every state with a nonempty set of worlds; < is anirreflexive and transitive relation on W. V is a valuation function V : U 7−→pow(ATM), which assigns to every world w the atoms holding in that world.For s ∈ S and A propositional, we let s |≡ A iff ∀w ∈ l(s)w |= A. Let Min<(A)be the set of minimal states s such that s |≡ A. We define M, s |≡ A |∼ B

iff ∀s′∈ Min<(A), then s

′|≡ B. We assume that < satisfies the smoothness

condition.

Let LL be a modal conditional language obtained by L by introducing anew modality L as follows: (i) if A is propositional, then A ∈ LL; LA ∈ LL;2¬LA ∈ LL, ¬2¬LA ∈ LL; (ii) if A, B are propositional, then A |∼ B ∈ LL;(iii) if A is a boolean combination of formulas of LL, then A ∈ LL.

We can map cumulative models into preferential structures with an addi-tional accessibility relation as defined below:

Definition 8 (CL-preferential structures). A model has the form M =〈W, R, <, V 〉 where: W is a non-empty set of items called worlds; R is a serialaccessibility relation; < is an irreflexive and transitive relation on W satisfyingthe smoothness condition; V is a function V :W 7−→ pow(ATM), which assignsto every world w the atomic formulas holding in that world. We add to the truthconditions for preferential models in Definition 1 the following clause:

M, w |= LA iff for all w′ | Rww′, w′ |= A

Moreover, we need to change the truth condition for conditional formulas asfollowsM, w |= A |∼ B if Min<(LA) ⊆ [LB].

We establish a correspondence between cumulative models (KLM) and CL-preferential models by showing that we are able to map cumulative modelsto CL-preferential models (and vice-versa) by preserving the satisfiability ofconditional formulas.


Proposition 2. A set of conditional formulas {(¬)A1 |∼ B1, . . . , (¬)An |∼ Bn} issatisfiable in a cumulative model 〈S, l, <, V 〉 iff it is satisfiable in a C-preferentialmodel 〈W, R, <, V 〉.

We will now present a tableaux calculus for CL. The calculus can be obtainedfrom the calculus T P for preferential logics, by adding a suitable rule for dealingwith the modality L. We define GL↓

= {A | LA ∈ G}.Our tableaux system T CL for CL is shown in Figure 5 and is obtained by

introducing the new modality L in the rules of T P and by adding the new rule(L−). Observe that rules (|∼+) and (|∼−) have been changed as they introduce themodality L in front of the propositional formulas A and B in their conclusions.The new rule (L−) is a dynamic rule.

(|∼+)G, A |∼ B

G,¬LA, A |∼ B G,¬�¬LA, A |∼ B G, LB, A |∼ B

(|∼−)G,¬(A |∼ B)

LA, �¬LA,¬LB, G|∼±

(L−)G,¬LA

where {¬LA} may be emptyG

L↓

,¬A

(�−)G,¬�A

G�

, G�↓

, G|∼±

,¬A, �A

Fig. 5. Tableaux system T CL. If ¬LA is not in the premise of (L−) (i.e. {¬LA} = ∅) the rule allows

to step from G to GL↓

. The boolean rules are omitted.

The proof of the completeness of the calculus can be done as for the prefer-ential case, provided we suitably modify the procedure for constructing a modelfor a finite consistent set of formulas G of LL. First of all, we need to modifythe definition of saturated sets.

Definition 9 (Saturated sets). A set of formulas G is saturated with respectto the static rules if, in addition to the conditions for boolean connectives inDefinition 4, the following conditions also hold:

• if A |∼ B ∈ G then ¬LA ∈ G or ¬�¬LA ∈ G or LB ∈ G;• if LA ∈ G then ¬L¬A ∈ G

For this notion of saturated set of formulas we can still prove Lemma 1 forlanguage LL.

Theorem 6 (Completeness of T CL). T CL is complete with respect to thesemantics.

Let us now analyze the calculus T CL in order to obtain a decision procedurefor CL logic. First of all, we reformulate the calculus as we made for P, obtaining


a system called T CLT. Rules for boolean connectives are the same as in T PT

(see Figure 4). The (|∼+) rule can be applied only if none of the subformulas ¬LA,¬�¬LA and LB are already in the current node. The (L−) rule is obviouslyapplicable only if {¬LA} ∪GL↓

6= ∅. (|∼−) and (�−) are not reformulated.In order to prove that T CLT ensures a terminating proof search we define a

measure m(G) =< c1, c2, c3, c3−4, c4 >, defined as in the case1 of T PT, with theaddiction of the index c3−4 defined as c3−4 =| {(¬)LA | (¬)LA ∈ G} |. Exactlyas we made for P, we consider a lexicographic order given by m(G), and easilyprove that each application of the rules of T CLT reduces this measure, as statedby the following:

Lemma 3. Consider an application of any rule of T CLT to a premise G andbe G

′any conclusion obtained; we have that m(G

′) < m(G).

Proof. Identical to the proof of Lemma 2. Just observe that if (L−) is applied,then c1, c2 and c3 are the same in both the premise and the conclusion, butc3−4 decreases, since (at least) one formula LA or ¬LA is removed from theconclusion. ut

By Lemma 3 we can conclude that T CLT ensures a terminating proof search.Moreover, we easily observe that the disjunction property holds in CL; there-fore, the algorithm described to give an explicit complexity bound for P can beused to prove that validity of CL is a CoNP problem. The algorithm is a nondeterministic algorithm which generates a branch of polynomial length and eval-uates in polynomial time with respect to the length of the initial set of formulasif the branch is closed (returning true) or not (returning false). The followinginstructions are situated between instructions 4. and 5.:

4’. if LA1, LA2, ..., LAu,¬LA1,¬LA2, ...,¬LAw ∈ G′

4’.1 G′←− (if w 6= 0) guess one ¬LAi and apply (L−) on it,

otherwise, if w = 0 and u 6= 0, then apply (L−); (O(1))4’.2 G

′←− guess one branch applying only propositional rules; (O(n))

Similarly to the case of P we conclude with the following:

Theorem 7 (Complexity of CL). Validity for CL is CoNP.

6 Conclusions

In this paper, we have presented some tableaux calculi for some of the KLMlogical systems for default reasoning. We have given a tableaux calculus for

1 These indexes are adapted considering the L modality; for instance, c2 is defined as follows: c2 =|{A |∼ B ∈+ G | �¬LA 6∈ G} |.


preferential logic P and for loop-cumulative logic CL. The calculi presentedgive a decision procedure for the respective logics, whose complexity is CoNPfor both P and CL.

Artosi, Governatori, and Rotolo [1] develop a labelled tableaux calculus fora flat fragment of the conditional logic CU, corresponding to the system C. Inthis paper, we do not treat this system but a stronger version of it, namely CL.Furthermore, as a major difference from our approach, the calculus proposed in[1] makes use of labels. The labels are introduced in order to represent possibleworlds or sets of possible worlds (for instance the label (W A, w) stands for anyworld in f(A, w)). In addition to the rules for dealing with ”declarative” for-mulas, they introduce a unification algorithm in order to deal with labels. As adifference from our calculus, the one proposed in [1] contains a cut-rule, calledPB, thus is not analytic, unless one can restrict the application of cut in ananalytic way. No matter whether or not cut is advantageous, it is clear that wecould incorporate it as a heuristic rule in our calculus.

In [7] it is defined a labelled tableaux calculus for the logic CE and someof its extensions. The flat fragment of CE corresponds to the system P. Thesimilarity between the two calculi lies in the fact that both approaches use amodal interpretation of conditionals. The major difference is that the calculuspresented here does not use labels, whereas the one proposed in [7] does. This isof course made possible by the fact that the language here is simpler that the onein [7], where there are nested conditionals. A further difference is in the logicsconsidered: whereas [7] considers CE and some stronger logics, we consider P(corresponding to CE) and the weaker CL.

Lehmann and Magidor [10] propose a non-deterministic algorithm that, givena finite set K of conditional assertions γi |∼ δi and a conditional assertion α |∼ β,checks if α |∼ β is not preferentially entailed by K. This algorithm tries to finda witness for a conditional assertion, i.e. a finite sequence of pairs (Ii, fi), whereIi are sets of indexes and fi are worlds in a preferential model. They prove thata conditional assertion α |∼ β has a witness iff it is not preferentially entailedby K. They conclude that preferential entailement is CoNP, thus obtaining acomplexity result similar to ours. However, it is not easy to compare their al-gorithm with our calculus, since the two approaches are radically different. Asfar as the complexity result is concerned, notice that our result is more gen-eral than theirs, since our language is richer: we consider boolean combinationsof conditional assertions (and also combinations with propositional formulas),whereas they do not. As remarked by Boutilier [2], this more general result isnot an obvious consequence of the more restricted one. Moreover, we prove theCoNP result also for the system CL. At the best of our knowledge, this resultwas unknown up to now.

In this paper we only consider two of the logical systems for nonmonotonicreasoning defined by KLM. We plan to extend our calculi to the other KLM


systems, namely to the weaker C and to the stronger R. For C we conjecturethat a complete calculus is given by a variant of T CL in which the (�−) rule isweakened so that it does not enforce the transitivity of the preferential relation<. Another development of our work will be the extension to first order case.The starting point will be the analysis of first order preferential and rationallogics by Friedman, Halpern and Koller in [5].

References

1. A. Artosi, G. Governatori, and A. Rotolo. Labelled tableaux for non-monotonic reasoning: Cu-mulative consequence relations. Journal of Logic and Computation, pages 12(6): 1027–1060, 2002.

2. C. Boutilier. Conditional logics of normality: a modal approach. Artificial Intelligence, 68(1),pages 87–154, 1994.

3. G. Crocco and P. Lamarre. On the connection between non-monotonic inference systems andconditional logics. In Proc. of KR ’92, pages 565–571, 1992.

4. N. Friedman and J. Y. Halpern. Plausibility measures and default reasoning. Journal of theACM, 48(4):648–685, 2001.

5. N. Friedman, J. Y. Halpern, and D. Koller. First-order conditional logic for default reasoningrevisited. ACM TOCL, ACM Press, 1(2):175–207, 2000.

6. D. Gabbay. Theoretical foundations for non-monotonic reasoning in expert systems. Logics andmodels of concurrent systems, Springer-Verlag New York, Inc., pages 439–457, 1985.

7. L. Giordano, V. Gliozzi, N. Olivetti, and C. Schwind. Tableau calculi for preference-based con-ditional logics. In Proc. of TABLEAUX 2003, volume 2796 of LNAI, Springer, pages 81–101,2003.

8. H. Katsuno and K. Sato. A unified view of consequence relation, belief revision and conditionallogic. In Proc. IJCAI’91, pages 406–412, 1991.

9. S. Kraus, D. Lehmann, and M. Magidor. Nonmonotonic reasoning, preferential models andcumulative logics. Artificial Intelligence, 44(1-2), pages 167–207, 1990.

10. D. Lehmann and M. Magidor. What does a conditional knowledge base entail? Artificial Intelli-gence, Elsevier Science Publishers Ltd., 55(1):1–60, 1992.

11. Y. Shoham. A semantical approach to nonmonotonic logics. In Proceedings of Logics in ComputerScience, pages 275–279, 1987.

Tableau-like Axiomatization for

Propositional Linear Temporal Logic ?

(Extended abstract of Position Paper)

Nikolay V. Shilov??

Department of Computer Science KAIST373-1 Kusong-dong Yusong-gu Daejeon 305-701, Korea,

[email protected]

Abstract. Propositional Linear Temporal Logic (PLTL) is a very popular formalismfor specification and verification of computer programs and systems. The paper suggestsa tableau-like axiomatization for PLTL based on automata-theoretic decision procedurecoupled with tableau for local model checking of the propositional µ-Calculus.

1 Introduction

Propositional Linear Temporal Logic (PLTL) is a very popular formalism forspecification and verification of computer programs and systems [17, 6]. Fun-damental results on decidability, model checking, and axiomatization for PLTLhave become a part of the Computer Science classics [10, 18]. Automata-theoretictechnique [20] has proved its utility for propositional modal logics of programs.In particular, PSPACE-completeness for PLTL has been proved in this tech-nique [19]. Later the automata-theoretic approach has been extended to modelchecking [6]. The axiomatization issues for PLTL have been studied first on baseof modal logic tradition [13]. But tableau and tableau-base decision procedurefor PLTL have been developed with aid of automata-theoretic technique [21].

After publication of [21], tableau for variants of linear temporal logic havebeen studied in a number of papers. A comprehensive study of tableaux for first-order temporal logics can be found in [14]. Tableau for combinations of temporallogics with other modal logics became a research topic in recent years [16, 9].

At the same time a so called clausal resolution approach for axiomatization ofdifferent propositional temporal logic was under development. General outlinesof this method has been presented in [11] for propositional linear temporal logicwith future and past modalities and operators. The method is based on classicalresolution augmented by temporal resolution rule. A special Separated NormalForm (SNF) has been defined for these purposes. For branching time temporal

? This work is supported by Brain Korea 21 Project, The school of information technology, KAISTin 0000.

?? While on leave from A.P. Ershov Institute of Informatics Systems, Lavren’ev av., 6, Novosibirsk630090, Russia

28 Nikolay V. Shilov

logic CTL a clausal resolution system has been developed in [1]. Algorithmicalissues of CTL resolution theorem prover have been discussed in [2]. The mostrecent development for branching time propositional logic is sound and completeclausal resolution system for ECTL+ [4]. For PLTL a sound and complete clausalresolution has been developed in [12] and then improved in [8]. Connectionbetween infinite automata and SNF has been examined in [3].

We develop in this paper a sound and complete experimental tableau-likeaxiomatization for PLTL. This axiomatization comprises rewriting rules thatsimplify formulae (table 1), and a ‘tableau’ (table 4). A deduction strategy withinthe axiomatization consists of a number of stages. These stages are sketchedbelow along with outlines of the rest of the paper. Basically our axiomatizationis ‘retrieved’ from automata-theoretic decision procedure. Implementation ofthe presented axiomatization and similar tableau-like axiomatization for otherpropositional program and temporal logics are topics for further research.

Section 2 introduces the rewriting rules that eliminate negations outsideliterals and emulate subformulae of until constructs U by new propositionalsymbols. The rules preserve tautologies and lead to a so-called simple formulae.

Section 3 studies a special class of automata on infinite words. An automatonin this class accepts an infinite word as soon as it enters any accepting controlstate. A (fairness) constraint is a set of input symbols. An infinite word meetsthe constraint iff all specified symbols occur finite number of times at most. Thehalting (termination) problem with the constraint consists in checking whetheran automaton accepts all infinite words that meet the constraint (if it is the casethan we say that the automaton totally accept the constraint).

Section 4 translates simple formulae of PLTL into automata with fairnessconstraint. Control states of the automata are finite sets of formulae. The mainproperty of this translation follows: a formula is a tautology iff the automatontotally accepts the constraint.

In section 5 the automata are considered as finite labeled transition systems(i.e. Kripke structures) for the propositional µ-Calculus [15], and the haltingproblem with constrains is encoded by a particular formula of the µ-Calculus.An automaton totally accepts a constraint iff the formula holds in some initialstate of the corresponding model. In simple words: we interpret halting problemwith fairness constraint as the local model checking problem for some fixedformula of the propositional µ-Calculus.

The last section 6 adopts sound and complete tableau designed for localmodel checking for the µ-Calculus in finite model [7] and convert it into atableau-like axiomatization of PLTL.

Acknowledgement: Author would like to thanks anonymous referees forvery detailed comments.

Tableau-like Axiomatization for Propositional Linear Temporal Logic 29

2 Propositional Linear Temporal Logic

Let Prp be an infinite set of propositional symbols.

Definition 1. The syntax of the Propositional Linear Time Logic (PLTL) con-sists of formulae that are defined by induction as follows:

– every propositional symbol is a formula;– negation (¬φ) is a formula;– conjunction (φ ∧ ψ) and disjunction (φ ∨ ψ) are formulae;– nextime (◦φ), always (�φ), and eventual (♦φ) are formulae;– until (φUψ) and unless (φWψ) are formulae.

Let Prp(ξ) be the set of all propositional symbols that occur in a formulaξ. Every substring of a formula that is a formula itself is said to a subformula.A literal is a propositional symbol or its negation. We exploit the standardabbreviations (φ→ ψ) and (φ↔ ψ) for ((¬φ)∨ψ) and for ((φ→ ψ)∧ (ψ → φ))respectively. Frequently we omit the most external parenthesis in small formulaeand some parenthesis inside formulae in accordance with the standard rules ofoperation precedence: ¬, ◦, �, ♦, ∧, ∨, →, ↔.

Definition 2. (Bounded) linear structure is pairs of the form (V,B) where

– the bound B ⊆ Prp is a finite set of propositional symbols,– the valuation sequence V is a countable sequence V0 ⊆ B, . . . Vi ⊆ B, . . ..

Definition 3. If (V,B) and (U,C) are two bounded linear structures such thatB ⊆ C and Vi = (Ui∩B) for every i ≥ 0, then (U,C) is said to be a (semantics)extension of (V,B) on (propositional symbols in) C \B.

Definition 4. A point is a triple of the form (V,B, i) where i ≥ 0 is an integerand (V,B) is a bounded linear structure.

Definition 5. Semantics of PLTL is defined in terms of the satisfyability rela-tion |= between points and formulae by induction on formula structure1:

– (V,B, i) |= p iff p ∈ Vi for p ∈ Prp;– (V,B, i) |= (¬φ) iff (V,B, i) |=/ φ;– (V,B, i) |= (φ ∧ ψ) iff (V,B, i) |= φ and (V,B, i) |= ψ,

(V,B, i) |= (φ ∨ ψ) iff (V,B, i) |= φ or (V,B, i) |= ψ;– (V,B, i) |= (◦φ) iff (V,B, i+ 1) |= φ,

(V,B, i) |= (�φ) iff (V,B, j) |= φ for every j ≥ i,(V,B, i) |= (♦φ) iff (V,B, j) |= φ for some j ≥ i;

– (V,B, i) |= (φUψ) iff (V,B, k) |= ψ for some k ≥ i and(V,B, j) |= φ for every j ∈ [i..k[,

(V,B, i) |= (φWψ) iff (V,B, i) |= (�φ) or (V,B, i) |= (φUψ).

1 We assume Prp(φ)∪ Prp(ψ) ⊆ B in this definition.


A formula is said to be a tautology iff it holds in every point. Formulae aresaid to be equivalent iff they have equal semantics (i.e. for every point they holdor do not hold in the point simultaneously). As usual, formulae φ and ψ areequivalent iff the formula (φ↔ ψ) is a tautology.

Definition 6. Normal formulae are formulae that do not use abbreviations →and ↔, and that can use the negation in literals only. Simple formulae are nor-mal formulae that do not use W operator and that can use U operator withpropositional symbols only.

Every PLTL formula is equivalent to some normal formula due to standard‘normalizing’ De-Morgan-like tautologies

¬¬φ ↔ φ ¬ ◦ φ↔ ◦¬φ¬�φ ↔ ♦¬φ ¬♦φ ↔ �¬φ¬(φ ∧ ψ) ↔ ¬φ ∨ ¬ψ ¬(φ ∨ ψ) ↔ ¬φ ∧ ¬ψ¬(φUψ) ↔ ¬ψW(¬φ ∧ ¬ψ) ¬(φWψ) ↔ ¬ψU(¬φ ∧ ¬ψ

The major disadvantage of this normalization is exponential space complexity(since it multiplies copies of some subformulae). We overcome this problem byshifting equivalence to metaequivalence as follows.

Definition 7. Formulae φ and ψ are metaequivalent ( φ<↔ ψ) iff for every

point (V,B, i) the following holds:

(V,B, i) |= φm

(U,C, i) |= ψ for every extension (U,C) of (V,B) on C \B.

The equivalence implies the metaequivalence but not vice versa. The metaequiv-alence is not symmetric, but metaequivalent formulae are tautologies or are nottautologies simultaneously.

A new (or fresh) propositional symbol is a symbol from infinite alphabetPrp that has not been used yet. Syntax substitution of some object instead of(any/all) instance(s) of some target in a subject is denoted by subjectobjecttarget.

Lemma 1.For every formula ξ, every its subformula θ that is out of scope of any negationin ξ, and every new propositional symbol p the formulae ξ and �(θ → p) → ξpθare metaequivalent: ξ

<↔ �(θ → p) → ξpθ .

Combining lemma 1 with tautology φWψ ↔ �φ ∨ (φUψ) and with thenormalizing tautologies we get the following proposition.

Proposition 1.Every formula is metaequivalent to some simple formula that can be constructedin polynomial time by the rewriting system presented in the table 1.


ζ ⇒ ζφ¬¬φ ζ → ζ◦¬φ¬◦φ

ζ ⇒ ζ↔♦¬φ¬�φ

ζ ⇒ ζ�¬φ¬♦φ

ζ ⇒ ζ¬φ∨¬ψ¬(φ∧ψ) ζ ⇒ ζ¬φ∧¬ψ

¬(φ∨ψ)

ζ ⇒ �((¬φ→ p) ∧ (¬ψ → q)) → ζ�p∨(pU(p∧q))

¬(φUψ)

ζ ⇒ �((¬φ→ p) ∧ (¬ψ → q)) → ζpU(p∧q)

¬(φWψ)

ζ ⇒ �((φ→ p) ∧ (ψ → q)) → ζpUqφUψ

ζ ⇒ �((φ→ p) ∧ (ψ → q)) → ζ�p∨(pUq)φWψ

(where p and q are new propositional symbols)

Table 1. Rewriting rules for simplification

3 Stuttering Automata with Fairness Constraint

Speaking informally, a stuttering automaton is just a nondeterministic finiteautomaton with the input alphabet consisting of subsets of some finite set, thatcan stutter (stay for awhile) on cells of the input tape.

Definition 8.A stuttering automaton is a tuple (Sts, Bnd, Ini, F in, Prg) where

– Sts is a finite set of control states, Ini and Fin are subsets of Sts thatcomprise initial and final states;

– Bnd is a finite set, called the bound, while the powerset 2Bnd is called theinput alphabet;

– Prg is the program that consists of transitions of 2 types:• reading type (q′, S) → q′′,• moving type (q′, S,next) → q′′,

where q′, q′′ ∈ Sts, S ⊆ Bnd, and next is a special reserved symbol.

The stuttering automata work on countable sequences of input symbols. Everysequence of this kind can be thought as input tape consisting of cells (or posi-tions) that are enumerated and that contain subsets of the bound set per cell.Every stuttering automaton has a pointer that every time points to a cell of theinput tape and can remains in this position or move to the next cell to the right.

Definition 9. Let (Sts, Bnd, Ini, F in, Prg) be a stuttering automaton. A con-figuration of the automaton is a triple (W, i, q) that comprises an infinite wordW ∈ (2Bnd)ω (input tape), an integer i ≥ 0 (pointer position), and a controlstate q ∈ Sts. We say that a configuration (W, i, q) contains the word W . Aconfiguration is said to be initial iff i = 0 and q ∈ Ini (i.e. the pointer is on theleftmost cell and the automaton is in an initial state). A configuration is said tobe final iff q ∈ Fin (the automaton is in a final state).

Definition 10. Let (Sts, Bnd, Ini, F in, Prg) be a stuttering automaton. Theautomaton shifts from one configuration to another in accordance with the pro-gram: it can shift from (W, i, q′) to


– (W, i, q′′) iff (q′,Wi) → q′′ ∈ Prg;– (W, (i+ 1), q′′) iff (q′,Wi,next) → q′′ ∈ Prg.

Definition 11. For a given stuttering automaton A shifting is a binary relation→A on its configurations: for every pair of configurations c′ abd c′′, we writec′ →A c′′ iff A can shift from c′ to c′′. We denote by →∗

A the reflexive andtransitive closure of the binary relation →A.

Definition 12. A stuttering automaton A accepts an infinite word W (writtenin its input alphabet) iff there are an initial configuration c′ and a final configura-tion c′′ such that c′ and c′′ both contain the word W and c′ →∗

A c′′. The languageof the automaton L(A) comprises all infinite words that the automaton accepts.The automaton A is said to be total iff L(A) comprises all infinite words (2B)ω.

Now we are going to define a very important notion of fairness constraint.

Definition 13. Let D be some set, seq ∈ Dω be an infinite sequence of elementsin D, and (P : D → Bool) be some property of elements in D. The sequence seqis said to be fair with respect to the property P iff infinitely many elements ofthe sequence seq enjoy this property. In contrast, we say that the sequence seqmeets a fairness constrain P iff the property P holds at most finitely often inseq (i.e. P does not hold after some point in seq).

We are most interested in some fairness constraint for stuttering automata.

Definition 14. Let Bnd be a finite set and S ⊆ Bnd. A competence propertyPS is the following property λT ⊆ Bnd. (S ∩ T 6= ∅).

The following lemma is straightforward.

Lemma 2. Let Bnd be a finite set, S ⊆ Bnd, and W ∈ (2Bnd)ω be an infiniteword. Then W meets fairness constraint PS iff all propositional symbols in Sdisappear after some position in W .

(It explains the title ‘competence property’ for PS: the fairness constraint PSgrants full rights to elements in Bnd \ S while imposes right limitations forelements in S; the former can occur infinitely often, the later – finitely often.)

Definition 15. Let (Sts, Bnd, Ini, F in, Prg) be a stuttering automaton, S ⊆Bnd, and PS be corresponding competence property. We say that the automatonA totally meets the fairness constraint PS iff language L(A) contains all infinitewords W ∈ (2B)ω that meet the constraint PS.

In conjunction with lemma 2 it immediately implies the following lemma.

Lemma 3. Let (Sts, Bnd, Ini, F in, Prg) be a stuttering automaton, S ⊆ Bnd,and PS be corresponding competence property. The automaton totally meets thefairness constraint PS iff it accepts every infinite word in (2Bnd)ω that containsfinite (at most) number of instances of symbols in S.


Definition 16.The total (halting, termination) problem for stuttering automata with compe-tence fairness constraint is to check for input stuttering automaton A and inputcompetence property PS whether the automaton A totally meets the fairness con-straint PS.

4 PLTL and Stuttering Automata

Below we present the algorithm of translation of simple formulae of PLTL tostuttering automata with fairness constraint. The algorithm inputs a simpleformula ξ and a set of propositional symbols B that includes all symbols thatoccur in ξ, and outputs a stuttering automaton A(ξ, B) and two sets of newpropositional symbols F (ξ, B) and G(ξ, B). The description of the algorithmfollows.

Let ξ be a simple formula and B ⊇ Prp(ξ) be a set of propositional symbols.Let us enumerate all instances of conjunctions ∧ and modalities � within ξ; itgives us an opportunity to index conjunctions and always modalities and referevery particular instance by the assigned index. Let C and A be set of indexesassigned to conjunctions and to � modalities by this enumeration. Let us assigna new propositional symbol fc for every conjunction ∧c (c ∈ C) and a newpropositional symbol ga for every modality �a (a ∈ A) within ξ. Let F (ξ, B) be{fc : c ∈ C} and G(ξ, B) be {ga : a ∈ A}.

The control states Sts of resulting automaton are subformulae of the for-mula ξ extended by a special state accept. The initial state is the formula ξ,the final state is accept: Ini = {ξ} and Fin = {accept}. The input alphabetbound Bnd is B ∪ F (ξ, B) ∪ G(ξ, B), i.e. the input alphabet comprises all setsof propositional symbols in B and new propositional symbols associated withconjunctions and�modalities in the formula ξ. The program Prg of the automa-ton A(ξ, B) is presented in the table 2 in structured and unstructured forms.In structured formalism we exploit ; for sequencing, U for non-deterministicchoice, * for non-deterministic iteration, if − then − else for deterministicchoice, while − do for deterministic iteration. We also use tests of two kinds:if p is a propositional symbol then the test p? means the p ∈ Wnow and the test¬p? means the p /∈ Wnow, where Wnow ⊆ B ∪ F (ξ, B) ∪G(ξ, B) is the currentlyreading position of the input word W .

Lemma 4.Let ξ be a simple formula and B ⊇ Prp(ξ) be a set of propositional symbols.Let F = F (ξ, B) and G = G(ξ, B) be two sets of new propositional symbols con-structed in accordance with the translation algorithm. Then for every subformulaθ of the formula ξ, for every point (V,B, i) the following holds:

(V,B, i) |= θ


(p, S) → accept iff p ∈ S P (p) = p? ; accept

(¬p, S) → accept iff p /∈ S P (¬p) = ¬p? ; accept

(◦φ,S,next) → φ P (◦φ) = next ; P (φ)

(�aφ,S,next) → �aφ iff ga ∈ S P (�aφ) = while ga? do next ; P (φ)(�aφ,S) → φ iff ga /∈ S

(♦φ,S) → φ P (♦φ) = next* ; P (φ)(♦φ,S,next) → ♦φ(φ ∧c ψ, S) → φ iff fc ∈ S P (φ ∧c ψ) = if fc then P (φ) else P (ψ)(φ ∧c ψ, S) → ψ iff fc /∈ S

(φ ∨ ψ, S) → φ P (φ ∨ ψ) = P (φ) U P (ψ)(φ ∧ ψ, S) → ψ

(pUq, S) → q P (pUq) = (p? ; next)* ; q? ; accept

(pUq, S,next) → pUq iff p ∈ S

Table 2. Automaton program and its structured flowchart

iffthe stuttering automaton

(

control states

︷︸︸︷

({accept} ∪ Sub(θ)) ,

bound

︷︸︸︷

(B ∪ F ∪G) ,

Ini states

︷︸︸︷

{θ} ,

Fin states

︷︸︸︷

{accept} ,

program

︷︸︸︷

P (θ))

starting in position i accepts every extension (V, B ∪ F ∪G) of (V,B)on propositional symbols in F ∪G that meets the fairness constraint PG.

(In plain words: θ holds in the point (V,B, i) iff the corresponding automatonaccepts every word (Vi ∪ Fi ∪ Gi), (Vi+1 ∪ Fi+1 ∪ Gi+1), . . . , where Fi, Fi+1,. . . ⊆ F and Gi, Gi+1, . . . ⊆ G but ∅ = Gj = Gj+1 = . . . for some j ≥ i.)

The above lemma immediately implies the following proposition.

Proposition 2.Let ξ be a simple formula and B ⊇ Prp(ξ) be a set of propositional symbols.Let F = F (ξ, B) and G = G(ξ, B) be two sets of new propositional symbolsconstructed in accordance with the translation algorithm. Then the followingholds:

ξ is a tautologyiff

the stuttering automaton(({accept} ∪ Sub(θ)) , (B ∪ F ∪G) , {θ} , {accept} , P (θ))

totally accepts the fairness constraint PG.

5 Model Checking Interpretation

Let {true, false} be Boolean constants, V ar and Act be disjoint finite alphabetsof propositional and action variables respectively. For avoiding ambiguities, weassume that these new alphabets V ar and Act are disjoint with the alphabet ofpropositional symbols Prp that are in use in PLTL.


Definition 17. The syntax of the propositional µ-Calculus (µC) consists of for-mulae that are defined by induction as follows:

– every propositional variable is a formula;– negation (¬φ) is a formula;– conjunction (φ ∧ ψ) and disjunction (φ ∨ ψ) are formulae;– (〈a〉φ) and ([a]φ) are formulae for every a ∈ Act;– the least (µx . φ) and the greatest (νx . φ) fixpoints are formulae for everyx ∈ V ar without instances in the range of odd amount of negations in φ.

As in the PLTL framework, sometimes we omit the most external parenthesisin small formulae and some parenthesis inside formulae in accordance with thestandard rules of boolean operation precedence. We also use syntax substitutionsubjectobjecttarget and extend it in the following manner: let subject0target(object) stay

for the object, and let subjectn+1target(object) stay for subject

subjectntarget(object)

target .Semantics of µC is defined in models that are called labeled transition sys-

tems in Computer Science or Kripke structures in modal logic tradition. Foravoiding ambiguities with PLTL, we use terminology and notation of modallogic for reasoning about µC.

Definition 18. Every model M is a triple (D,R,E) where the universe D 6= ∅consists of worlds, the interpretation R : Act → 2D×D assigns a binary relationR(a) ⊆ D ×D to every action variable a, the evaluation E : V ar → 2D assignsa monadic predicate E(x) ⊆ D to every propositional variable x.

Models can be infinite, but we are most interested in finite models only.

Definition 19.Semantics of µC is a ternary validity relation ||= between worlds, models, andformulae. This relation is defined by induction on formulae structure. In finitemodels it can be defined as follows:

– w||=M true and w||=/ Mfalse,w||=M x iff w ∈ E(x) for x ∈ V ar;

– w||=M (¬φ) iff w||=/ Mφ;– w||=M (φ ∧ ψ) iff w||=M φ and w||=M ψ,w||=M (φ ∨ ψ) iff w||=M φ or w||=M ψ;

– w||=M ([a]φ) iff u||=M φ for every u such that (w, u) ∈ R(a),w||=M (〈a〉φ) iff u||=M φ for some u such that (w, u) ∈ R(a);

– w||=M νx.φ iff w||=M φnx(true) for all n ≥ 0;w||=M µx.φ iff w||=M φnx(false) for some n ≥ 0.

Model checking is testing a model against a formula. In particular, the localchecking problem consists in testing the validity w||=M ξ of the input formulaξ in the input world w in the input model M . We are most interested modelchecking of finite models.


Definition 20. Let x, y, Nice, and Fin be fixed propositional variables, andA,B ⊆ Act be sets of action variables. Then let

– GOOD be formula (Nice ∧∧

b∈B〈b〉y),– HALT be formula (Fin ∨ x ∨

∧

a∈A〈a〉x),

– PROVER be formula (ν y.GOOD)(µ x.HALT )Nice .

We are especially interested in the model checking PROVER in models thatare generated by stuttering automata with constraint.

Definition 21. Let A = (Sts, Bnd, Ini, F in, Prg) and PS be particular stut-tering automaton and competence property. Let M be the set of control statesthat occur in the right hand side of moving transitions.

– First, for every T ⊆ Bnd let us define a binary relationT on Sts×(M∪Fin):

q′T q′′

iffq′ ≡ q′′ ∈ Fin or

there is some sequence of control states q0, . . . qn (n ≥ 0) such thatq′ = q0, (q0, T ) → q1 ∈ Prg, . . . (qn−1, T ) → qn ∈ Prg, and

(qn, T,next) → q′′ ∈ Prg.

– Then let us extendT on 2Sts × 2M∪Fin as follows:

Q′ T Q′′

iff

for every q′′ ∈ Q′′ there is some q′ ∈ Q′ such that q′T q′′.

Definition 22. Let A = (Sts, Bnd, Ini, F in, Prg) and PS be a stuttering au-tomaton and a competence property. Let M(A,PS) be the following finite model(D,R, E). The universe D is 2Sts, i.e. comprises all sets of control states. Thealphabet Act of action variables coincides with the input alphabet of the automa-

ton: Act = 2Bnd; for every T ∈ Act let R(T ) beT . The alphabet of propositional

variables V ar includes one ‘special’ variable Fin and two auxiliary variables x,y; evaluation of the special variable is E(Fin) = 2Fin, i.e. it comprises all sub-sets of the final sets. The model checking interpretation for the total problemfor the automaton A with the fairness constraint PS consists in the finite modelM(A,PS) and two sets 2Bnd and 2Bnd\S adopted as A ⊆ Act and B ⊆ Act inthe formula PROVER.

The importance of the model checking interpretation follows from the followingproposition.

Proposition 3.

A stuttering automaton A totally accepts a fairness constraint PS

iffQ||=M(A,PS) PROVER for some set Q of initial control states of A.


6 Axiomatization via Local Model Checking

There are two papers [7, 5] that have suggested tableau for local model checkingof formulae of the propositional µ-Calculus. The first cited paper addresses finitestate systems, while the second one deals with infinite systems as well as finite.We prefer system from [7] since we are interested in model checking interpreta-tion of the halting problem with fairness constraint, i.e. we are bound by finitemodels M single formula PROV ER. In the following paragraphs we sketch theapproach, the tableau, and soundness and completeness results from [7].

There are only 2 syntax differences between variants of the propositional µ-Calculus, that was discussed in the section 5 and that is in use in [7]. First, theset of propositional variable in [7] is divided on two disjoint sets: the variablesthat can not be bound by fixpoints and the variables that have to be bound byfixpoints; the former we refer as model constants, the later – as model variables.Next, [7] exploits syntax without ∧, [ ], and µ. Both variants enjoy equal expres-sive power due to standard De-Morgan-like tautologies: φ ∧ ψ ↔ ¬(¬φ ∨ ¬ψ),[a]φ↔ ¬〈a〉¬ψ, µx.ψ ↔ ¬(νx.(ψ¬x

x )). For avoiding ambiguities, we distinguishthese two variants and refer variant from [7] by acronym νC.

In particular, in the formula PROVER propositional variable Fin is a modalconstant and propositional auxiliary variables x and y are modal variables. νC-representation of this formula is the following formula νPROVER:

νy.¬(

νx.¬(

φ(x)︷︸︸︷

Fin ∨ ¬x ∨ ¬(∨

T⊆Bnd\S

¬(〈T 〉¬x)))

∨ (∨

T⊆Bnd

¬(〈T 〉y))

︸︷︷︸

ψ(y)

)

.

The subformula relation (‘strict subterm’ in [7]) ≺ is treated in pure syntaxmanner like in PLTL: a subformula is a substring of the formula that is a formulaitself. The complete graph of the immediate subformula relation for subformulaeof νPROVER is depicted in the figure 1.

The tableau from [7] is represented in the table 3. We only turned upside-down all rules so that the goals are under subgoals (since we prefer proof-searchtree to grow upward). The proof rules operate on sequents of the form (H `Mw ∈ ξ) where ξ is a formula of νC, M is a finite model, w is a world and H is aset of hypothesis (or assumptions) of the form (u : θ) where u is a world and θ isa closed fixpoint formula. [7] has proved the general soundness and completenessresults (theorems 4.18 and 4.19). We would like to summarize them both in thefollowing corollary.

Corollary 1.For every formula ξ of νC, for every finite model M and every world w withinthis model the following holds: ∅ `M w ∈ ξ iff w||=M ξ.


νy.¬ψ(y)↓

¬ψ(y)↓ψ(y)

↙ ↘νx.¬φ(x) ¬(〈T 〉y) for every

T ⊆ Bnd

↓ ↘¬φ(x) 〈T 〉y

↙ ↓ ↘ ↘¬(

W

T⊆Bnd\S(¬〈T 〉¬x)) Fin ¬x y↙ ↗ ↘

W

T⊆Bnd\S(¬〈T 〉¬x) ↗ x↙ ↗

¬〈T 〉¬x for everyT ⊆ Bnd \ S

→ 〈T 〉¬x

Fig. 1. Subformulae of νPROV ER

Axiom Schemata

H `M w ∈ p iff p is a modal constant and w ∈ E(p)

H `M w ∈ ¬p iff p is a modal constant and w /∈ E(p)

H `M w ∈ ¬(〈a〉ξ) iff {v : (w, v) ∈ R(a)} is empty set ∅H `M w ∈ νx.ξ iff (w : νx.ξ) ∈ H

Inference RulesH`Mw∈ξ

H`Mw∈¬¬ξH`Mw∈¬ξ , H`Mw∈¬θ

H`Mw∈¬(ξ∨θ)H`Mw∈ξH`Mw∈ξ∨θ

H`Mw∈θH`Mw∈ξ∨θ

H`Mu∈ξH`Mw∈〈a〉ξ

for u ∈ {v : (w, v) ∈ R(a)}H`Mu1∈¬ξ ,... H`Mun∈¬ξ

H`Mw∈¬(〈a〉ξ)where {u1, . . . un} = {v : (w, v) ∈ R(a)}

H′∪{(w:νx.ξ)}`Mw∈ξνx.ξx

H`Mw∈νx.ξwhere (w : νx.ξ) /∈ H and H ′ = H \ {(u : θ) : νx.ξ ≺ θ}

H′∪{(w:νx.ξ)}`Mw∈¬ξνx.ξx

H`Mw∈¬(νx.ξ)where (w : νx.ξ) /∈ H and H ′ = H \ {(u : θ) : νx.ξ ≺ θ}

Table 3. Sound and complete system for local model checking from [7]

At last we are ready to present tableau-like deduction system in the table 4.This system is bound for a target simple PLTL formulae to be proved η. In thissystem

– W and U range over sets of subformulae of η extended by label accept,– H and H ′ range over collections of assumptions in the form (W : νy.¬ψ(y))

or (U : νx.¬φ(x)), where νy.¬ψ(y) and νx.¬φ(y) are the only two closedformulae in fig. 1,

– T ranges over sets of Prp(η) ∪ F (η, Prp(η)) ∪ G(η, Prp(η)) (i.e. are sets ofpropositional symbols, conjunctions and always-modalities in η),

–T is the binary relation on sets of subformulae of η extended by label accept,derived from the table 2,

– ξ and θ range over νC-formulae in fig. 1 with Bnd = (Prp(η)∪F (η, Prp(η))∪G(η, Prp(η)) and S = G(η, Prp(η),

– ≺ is the subormula relation in fig. 1.


Axiom Schemata

H ` W ∈ Fin iff W = {accept}

H `W ∈ ¬(〈T 〉ξ) iff {U : WT U} is the emptyset

H `W ∈ νz.ξ iff (W : νz.ξ) ∈ H

Inference Rules

H`W∈ξ

H`W∈¬¬ξ

H`W∈¬ξ , H`W∈¬θ

H`W∈¬(ξ∨θ)H`W∈ξ

H`W∈ξ∨θH`W∈θ

H`W∈ξ∨θ

HÙ∈ξ

H`W∈〈T 〉ξ for some U that WT U

HÙ1∈¬ξ ,... HÙn∈¬ξH`W∈¬(〈T 〉ξ) where {U1, . . . Un} = {U : W

T U}

H ′∪{(W :νz.ξ)}`W∈ξνz.ξz

H`W∈νz.ξ

H ′∪{(W :νz.ξ)}`W∈¬ξνz.ξz

H`W∈¬(νz.ξ)where (W : νz.ξ) /∈ H and H ′ = H \ {(U : θ) : νz.ξ ≺ θ}

Table 4. Sound and complete system for simple formulae of PLTL

Combining propositions 1, 2, and 3 with corollary 1 we prove the followingsoundness and completeness theorem.

Theorem 1.

– For all formulae ζ and η of PLTL, if ζ can be transformed to η by rewritingrules in the table 1, then ζ is a tautology iff η is a tautology.

– Every formula ζ of PLTL, can be transformed by rewriting rules in the table1 to some simple formula η of PLTL.

– For every simple formula η of PLTL the following holds: η is a tautology iffthe sequent (∅ ` {η} ∈ νPROV ER) is provable in the system presented inthe table 4.

References

1. Bolotov A. and Fisher, M.: A Resolution Method for CTL Branching-Time Temporal Logic. InProceedings of the Fourth International Workshop on Temporal Representation and Reasoning


(TIME), IEEE Press, p.20-27, 1997.2. Bolotov A. and Dixon, C.: Resolution for Branching-Time Temporal Logics: Applying the Temporal

Resolution Rule. In Proceedings of the Seventh International Workshop on Temporal Representa-tion and Reasoning (TIME’00). IEEE Computer Press, p.163-172. 2000.

3. Bolotov A., Fisher M., and Dixon C.: On the Relationship Between Omega-Automata and Tem-poral Logic Normal Forms. Journal of Logic and Computation 12(4):561-581, 2002.

4. Bolotov A., Basukoski A.: Clausal Resolution for Extended Computation Tree Logic ECTL+. InProceedings of the Time 2004 International Conference on Temporal Representation and Reason-ing, IEEE Computer Press, 2004.

5. Bradfield J., Stirling C.: Local model checking for infinite state spaces. Theoretical ComputerScience, 96:157-174, 1992.

6. Clarke E.M., Grumberg O., Peled D.: Model Checking. MIT Press, 1999.7. Cleaveland R.: Tableau-based model checking in the propositional mu-calculus. Acta Informatica,

27:725–747, 1990.8. Degtyarev A., Fisher M., and Konev B.: A Simplified Clausal Resolution Procedure for Proposi-

tional Linear-Time Temporal Logic. In Proc. TABLEAUX-02. Springer-Verlag, Lecture Notes inComputer Science 2381: 85-99, 2002.

9. Dixon C., Nalon C., and Fisher M.: Tableaux for Temporal Logics of Knowledge: SynchronousSystems of Perfect Recall or No Learning. In Proceedings of TIME-ICTL 2003, IEEE CS Press.

10. Emerson E.A.: Temporal and Modal Logic. In Handbook of Theoretical Computer Science, v.B,Elsilver and The MIT Press, 1990, p.995-1072.

11. Fisher M.: A Resolution Method for Temporal Logic. In Proceedings of Twelfth InternationalJoint Conference on Artificial Intelligence (IJCAI). Sydney, Australia, August 1991. Published byMorgan Kaufmann. ISBN 1-55860-160-0

12. Fisher, M., Dixon, C., and Peim, M.: Clausal Temporal Resolution. ACM Transactions on Com-putational Logic 2(1):12-56, 2001.

13. Gabbay D.M., Pnueli A., Shelah S., Stavi J.: On the temporal analysis of fairness. In 7th ACMSymposium on Principles of Programming Languages, Las Vegas, p. 163-173, 1980.

14. Kontchakov, R., Lutz, C., Wolter, F., and Zakharyaschev M.: Temporal Tableaux. Studia Logica,76(1):91-134, 2004.

15. Kozen, D.: Results on the Propositional Mu-Calculus. Theoretical Computer Science, 27:333-354,1983.

16. Lutz, C., Sturm, H., Wolter, F., and Zakharyaschev, M.: Tableaux for Temporal DescriptionLogic with Constant Domain. In Proceedings of the International Joint Conference on AutomatedReasoning IJCAR-01, Springer Verlag Lecture Notes in Artifical Intelligence, 2083:121-136, 2001.

17. Manna Z., Pnueli A.: The temporal logic of Reactive and Concurrent Systems. Springer-Verlag,1991.

18. Stirling C.: Modal and Temporal Logics. In Handbook of Logic in Computer Science, v.2, ClaredonPress, 1992, p.477-563.

19. Vardi, M.Y.: An automata-theoretic approach to linear temporal logic. In Logics for Concurrency:Structure versus Automata, Springer-Verlag, Lecture Notes in Computer Science 1043:238-266,1996.

20. Vardi, M.Y., Wolper, P.: Automata-theoretic techniques for modal logic of programs. J. Computerand System Sciences 32:183-221, 1986

21. Wolper, P.: The tableau method for temporal logic: An overview. Logique et Analyse, 28:119-136,1985

Instance Based Methods

Peter Baumgartner1 and Gernot Stenz2

1 Programming Logics GroupMax-Planck-Institut fur Informatik

[email protected]

2 Institut fur InformatikTechnische Universitat Munchen

[email protected]

The term “instance based methods” (IBM) refers to a family of methods forfirst-order logic theorem proving. IBMs share the principle of carrying out proofsearch by maintaining a set of instances of input clauses and analyzing it for sat-isfiability until completion. IBMs are conceptually essentially different to wellestablished methods like resolution or free-variable analytic tableaux. Also, IBMsexhibit a search space and termination behaviour (in the satisfiable case) differ-ent from those methods, which makes them attractive from a practical point ofview as a complementary method. This observation is also supported empiricallyby results obtained with the first serious implementations available (carried outby Letz and Stenz, cf. the system competitions (CASC) at CADE-18, CADE-19and CADE-20).

The idea behind IBMs is already present in a rudimentary way in the workby Davis, Putnam, Logemann and Loveland in the early sixties. The contempo-rary stream of research on IBMs was initiated with the Plaisted’s Hyperlinkingcalculus in 1992. Since then, other methods have been developed by Plaisted andhis coworkers. Billon’s disconnection calculus was picked up by Letz and Stenzand has been significantly developed further since then. New methods have alsobeen introduced by Hooker, Baumgartner and Tinelli, and more recently byGanzinger and Korovin. The stream of publications over the last years demon-strates a growing interest in IBMs. The ideas presented there show that researchon IBMs still is in the middle of development, and that there is high potentialfurther improvements and extensions like equality and theory handling, whichis currently investigated.

Contents

In the tutorial, we will cover the following topics: Early IBMs, the commonprinciple behind IBMs; classification of IBMs (one-level vs. two-level calculi),comparison to resolution and free variable tableaux; selected IBMs in greaterdetail: ordered semantic hyper linking, the disconnection method, the modelevolution calculus; the completeness proof of one selected method; extension toequality reasoning; implementation techniques, particularly the disconnectionmethod.

42 Peter Baumgartner and Gernot Stenz

Presenters

Peter Baumgartner has (co-)authored 13 journal articles, 31 conference or re-ferred workshop papers, and five chapters in books. Most publications are con-cerned with calculi, implementations and applications of first-order logic au-tomated deduction systems. He developed a First-Order version FDPLL ofthe propositional Davis-Putnam-Logemann-Loveland procedure. This method,and its successor, the Model Evolution Calculus (jointly developed with CesareTinelli) are his recent main contributions to instance based methods.

Gernot Stenz has been directly involved in instance based theorem provingfor several years. He is the (co-)author of 15 scientific papers and system de-scriptions at international conferences and some other publications in journalsand books. Nearly all of his more recent publications deal with instance basedtheorem proving in general and the disconnection calculus in particular. Theimplementation of theorem prover systems is among his principal matters ofinterest, he was a co-author of the e-SETHEO prover system, where his workalso included automated learning methods for theorem provers and he has beendeveloping and improving the DCTP theorem prover implementation of the dis-connection calculus. Both of these systems have won trophies at the annualCADE theorem prover competitions.

References

1. Peter Baumgartner and Cesare Tinelli. The Model Evolution Calculus. In Franz Baader, editor,Automated Deduction – CADE-19, volume 2741 of Lecture Notes in Artificial Intelligence. Springer,2003.

2. Peter Baumgartner. FDPLL – A First-Order Davis-Putnam-Logeman-Loveland Procedure. InDavid McAllester, editor, Proceedings of the 17th International Conference on Automated Deduc-tion (CADE-17), Pittsburgh, USA, volume 1831 of Lecture Notes in Artificial Intelligence, pages200–219. Springer, 2000.

3. J.-P. Billon. The disconnection method: a confluent integration of unification in the analyticframework. In Proceedings, 5th TABLEAUX, volume 1071 of LNAI, pages 110–126, Berlin, 1996.Springer.

4. Harald Ganzinger and Konstantin Korovin. New directions in instantiation-based theorem proving.In Proceedings of the eightteenth Annual IEEE Syposium on Logic in Computer Science (LICS-03)9, pages 55–64, Los Alamitos, CA, June 22–25 2003. IEEE Computer Society.

5. J. Hooker, G. Rago, V. Chandru, and A. Shrivastava. Partial instantiation methods for inferencein first-order logic. Journal of Automated Reasoning, 28(5):371–396, 2002.

6. R. Letz and G. Stenz. Proof and Model Generation with Disconnection Tableaux. In Proceedings,LPAR 2001, pages 142–156. Springer, Berlin, 12/2001.

7. R. Letz and G. Stenz. Integration of Equality Reasoning into the Disconnection Calculus. InProceedings, TABLEAUX-2002, LNAI 2381, pages 176–190. Springer, Berlin, 7/2002.

8. S.-J. Lee and D. Plaisted. Eliminating duplication with the hyper-linking strategy. Journal ofAutomated Reasoning, pages 25–42, 1992.

9. David A. Plaisted and Yunshan Zhu. Ordered semantic hyper linking. Journal of AutomatedReasoning, 25(3):167–217, 2000.

Analytic Systems and Dialogue Games(Tutorial Description)

Christian G. Fermuller

Formal Logic GroupTechnische Universitat Wien, Austria

http://www.logic.at/people/chrisf

1 Introduction

Already in 1950s Paul Lorenzen introduced a strategic two person game in whichone player tries to defend a statement of arbitrary logical complexity against rationalattacks by the other player. The rules of the game were intended to capture the mean-ing of the logical particles and to serve as a foundation for constructive reasoning. Ittook many years before the exact relation between Lorenzen’s game and Gentzen’sfamous sequent calculus LI for intuitionistic logic had been clarified; but nowadaysa host of similar games and corresponding analytic proof systems for various formsof logics can be found in the literature. In fact, one may argue that Lorenzen’s foun-dational concept, if freed from the sole preoccupation with constructive reasoning,relates more directly to analytic reasoning and, in particular, tableau style calculi forclassical as well as many non-classical logics than other frameworks like, e.g., Tarski-style semantics.

In this tutorial we will circumvent the more abstract forms of dialogue gamesthat have become popular in so-called game semantics for linear logic and functionalprogramming languages, and rather build directly on Lorenzen’s original game. Wepresent different generalizations of it and explain their connection to well known aswell as less well known analytic calculi for intuionistic, intermediate logics and fuzzylogics.

More exactly, we want to provide a guided tour through the varied landscape ofsequent and hypersequent systems and corresponding versions of dialogue games thatwill highlight the following topics:

– The relation between Lorenzen’s dialogue game and Gentzen’s sequent calcu-lus LI.

– Parallel versions of Lorenzen’s game and corresponding hypersequent systems forintermediate logics.

– Dialogue games as models of (possibly distributed) proof search.– Model building, so-called sequents-of-relations systems and a dialogue game for

Godel-Dummett logic.– Giles’s game for Lukasiewicz logic and its relation to recent proof theoretic results

in t-norm based fuzzy logics.

44 Christian G. Fermuller

Given the wide scope of the area the goal is to provide an overview over somerelevant ideas and results rather than to get involved with many details.

2 Lorenzen style dialogue games and Gentzen’s LI

Following Paul Lorenzen we identify logical validity of a formula A with the existenceof a winning strategy for a proponent P in an idealized confrontational dialogue, inwhich P tries to uphold A against systematic doubts(‘attacks’) by an opponent O.

Remark. Although the game can be generalized to first order logic, we will stickto the propositional level throughout the tutorial.

Notation. An atomic formula (atom) is either a propositional variable or ⊥ (fal-sum). Compound formulas are built up from atoms using the connectives ⊃, ∧, ∨; ¬Aabbreviates A ⊃⊥. In addition to formulas, the special signs ?, l?, r? can be stated ina dialogue by the players P and O, as specified below.

Dialogue games are characterized by two sorts of rules: logical ones and struc-tural ones. The logical rules define how to attack a compound formula and how todefend against such an attack. They are summarized in the following table. (If X isthe proponent P then Y refers to the opponent O, and vice versa.1)Logical dialogue rules:

X: attack by Y defence by XA∧B l? or r? (Y chooses) A or B, accordinglyA∨B ? A or B (X chooses)A ⊃ B A B

O may also attack atoms (including ⊥) by stating ‘?’.A dialogue is a sequence of moves, which are either attacking or defending state-

ments, in accordance with the logical rules.Structural rules regulate the succession of moves. The following rules, together

with the winning conditions stated below, amount to a version of dialogues tradition-ally called Ei-dialogues (i.e., Felscher’s E-dialogues combined with the so-called ipsedixisti rule; see, e.g., [23]).Structural dialogue rules:Start: The first move of the dialogue is carried out by O and consists in an attack on

the initial formula.Alternate: Moves strictly alternate between players O and P.Atom: Atomic formulas, including ⊥, may be stated by both players, but can neither

be attacked nor defended by P.E: Each (but the first) move of O reacts directly to the immediately preceding move

by P.

Winning conditions (for P):1 Note that both players may launch attacks as well as defending moves during the course of a dialogue. For

motivation and detailed exposition of these rules we refer to [15].

Analytic Systems and Dialogue Games 45

W: The game ends with P winning if O has attacked a formula that has already beengranted (either initially or in a later move) by O.

W⊥: The game ends with P winning if O has granted ⊥.

Strategies are represented as trees whose branches are possible dialogues. Theadequateness of the sketched game for intuitionistic logic is shown by translatingwinning strategies into cut-free LI′-proofs and vice versa, where LI′ is a (proof searchfriendly!) variant of Gentzen’s LI that allows principal formulas of left hand side rulesalso to appear in the premises and shifts all weakenings to the axiom sequents. (Fordetails see, e.g., [18].)

3 Hypersequent calculi and parallel dialogues

A hypersequent is (here) defined as a finite, non-empty multiset of LI′-sequents,called components; written in the form

Γ1 −→C1 | . . . | Γn −→Cn.

The symbol “|” is intended to denote disjunction at the meta-level.The logical rules of a hypersequent calculus refer to individual components and

remain unchanged with respect to the underlying sequent calculus. However addi-tional external structural rules allow to manipulate more than one component at atime.

The hypersequent framework allows one to define analytic calculi for severalimportant intermediate logics. These include Godel-Dummett logic G∞ (also calledLC) [12, 20], finite-valued Godel logics Gn [20], and the logic LQ of weak excludedmiddle [22], also called Jankov logic in reference to [22]. Adequate calculi are ob-tained by adding just one structural rule, respectively, to the basic hypersequent calcu-lus for intuitionistic logic. E.g., a hypersequent calculus for G∞ is obtained by addingthe following rule (a version of which has been defined in [4]) in which H stands foran arbitrary ‘side hypersequent’:

Π1,Π2 −→C1 | H Π1,Π2 −→C2 | HΠ1 −→C1 | Π2 −→C2 | H

(com)

To extend the close correspondence between analytic sequent proofs and winningstrategies for Lorenzen style dialogues to the hypersequent level one introduces paral-lel versions of the basic intuitionistic dialogue game of Section 2 (I-game), that sharethe following features:

1. The logical and structural rules of the I-game remain unchanged. Indeed, ordinaryI-game dialogues appear as sub-case of the more general parallel framework.

2. The proponent P may initiate additional I-dialogues by ‘cloning’ the dialoguesequent of one of the parallel I-dialogues, in which it is her turn to move.


3. To win a set of parallel dialogues the proponent P has to win at least one of thecomponent dialogues.

This framework allows to define rules for the exchange of information betweenindividual I-dialogues. More exactly, various forms of synchronization between I-dialogues are formalized as the merging of two or more dialogues into a single di-alogue, according to the following general principle: P selects a certain number P-components, i.e., actual states of I-dialogues in which it is P’s turn to move. Thepicked components are then replaced by a new state of a merged dialogue in someparticular way. For some synchronization rules, there are different possible ways tomerge the components picked by P. In those cases O may choose from those pos-sibilities. As an example we state the synchronization rule that corresponds to thehypersequent rule (com), stated above, and consequently leads to a characterizationof G∞ in terms of parallel dialogues:

P-part: P picks two P-components Π1 `C1 and Π2 `C2 from the current global statefor merging; Π1∪Π2 will be the granted formulas of the merged dialogue sequent.

O-part: In response, O chooses either C1 or C2 as the active formula of the mergedcomponent, that is to be defended by P.

Here Π ` C denotes a state of a component dialogue, in which O has granted allformulas in Π and C is the active formula, which is the last formula that has beenstated by P and that either already has been attacked or must be attacked in O’s nextmove in that component dialogue.

All of the above mentioned intermediary logics, but also classical logic itself,can be characterized by similar parallel versions of Lorenzen’s dialogue game, usingadequate synchronization rules.

4 Dialogue games as models of proof search

To provide a general, rigorous, and useful mathematical analysis of proof searchstrategies is a great challenge; in particular if also the degree of possible paralleliza-tion of proof search is in focus. For classical logic, models for some types of proofsearch, including distributed search, have been presented (see, e.g., [7, 8]). But fornon-classical logics no analogous analysis of generic proof search strategies has beenattempted yet. In the tutorial we will argue, following [17], that (parallel) dialoguegames might serve as a versatile tool for that purpose.

To see how dialogue games are useful in modelling proof search, one better in-terprets a dialogue as a collaborative effort to check the validity of a formula, ratherthan as a confrontational dialogue between P and O. Borrowing terminology fromAndreas Blass [3] (who in turn credits unpublished work of Dexter Kozen) we mayspeak of P as a client, who wants to check whether a formula F follows from givenassumptions G1, . . . ,Gn, that are provided initially by the server O.


As we have seen, winning strategies for the client P in Lorenzen’s game corre-spond to analytic proofs for intuitionistic logic. Proof search strategies, i.e., strategiesthat aim at the explicit (and efficient) construction of a proof, correspond to uniformwinning strategies for P in the dialogue game. By this we mean generic winningstrategies that are parameterized by the formulas on which a concrete instance of thegame is to be played. As an example we mention that the strategies for intuitionisticproof search described in [28] can be modelled as preferences of choice among P’spossible moves in a dialogue.

The aptness of the dialogue game framework for the formalization of proof searchstrategies for a wide variety of intermediary logics becomes apparent if the synchro-nizing rules mentioned in Section 3 are interpreted as scheduling mechanisms in dis-tributed proof search.

5 A Dialogue game for model building in Godel-Dummett logic

To mention yet another use of dialogue games in automated deduction we plan topresent a version of a game for Godel-Dummett logic G∞ that has been introducedin [19]. When considered as a fuzzy logic, G∞ is characterized by interpretations vof the propositional variables in the real closed unit interval [0,1], and the followingextension of interpretations to compound formulas:

v(A∧B) = min(v(A),v(B)) v(⊥) = 0

v(A∨B) = max(v(A),v(B)) v(>) = 1 v(A ⊃ B) =

{

1 if v(A) ≤ v(B)v(B) otherwise

As can be seen from these definitions, the validity/satisfiability of formulas in G∞ onlydepends on the relative order of truth values assigned to the propositional variables,but not on their absolute value. This property allows one to determine logical validityin G∞ solely by referring to comparisons of values of (sub)formulas. For this purpose,we define a somewhat different type of game, which is based on the idea that anylogical connective ◦ of G can be characterized via an adequate response by a player Xto player Y’s attack on X’s claim that a statement of form (A ◦B)�C or C � (A ◦B)holds, where � is either < or ≤.

Notation. An assertion F �G is atomic if both, F and G, are atoms; otherwise it isa compound assertion. Atomic assertions of form A < A, A < ⊥, > < A or >≤⊥ arecalled elementary contradictions. An elementary order claim is a set of two assertionsof form {E �1 F,F �2 G}, where E, F , and G are atoms, and �1,�2 ∈ {<,≤}.

Following the tradition initiated by Lorenzen, we call the player that initiallyclaims the validity of a chosen formula the Proponent P, and the player that tries torefute this claim the Opponent O. The dialogue game proceeds in rounds as follows:

1. A dialogue starts with P’s claim that a formula F is valid. O answers (‘attacks’)by contradicting this claim with the assertion F < >.


2. Each following round consists in two steps:(i) P either attacks a compound assertion or an elementary order claim, contained

in the set of assertions that have been made by O up to this state of the dia-logue, but that have not yet been attacked by P.

(ii) O answers to the attack by adding a set of assertions according to the following

Rules for compound claims:

P attacks O asserts as answer

A∧B�C {A�C} or {B�C}C �A∧B {C �A, C �B}

A∨B�C {A�C, B�C}C �A∨B {C �A} or {C �B}

A ⊃ B < C {B < A, B < C}C < A ⊃ B {C < B} or {A ≤ B, C < >}A ⊃ B ≤C {> ≤C} or {B < A,B ≤C}C ≤ A ⊃ B {A ≤ B} or {C ≤ B}

Rules for elementary order claims:

P attacks O asserts as answer

{A ≤ B, B ≤C} {A ≤C}{A < B, B�C} {A < C}{A�B, B < C} {A < C}

3. The dialogue ends with P as winner if O has asserted an elementary contradiction.Otherwise, O wins if there is no further possible attack for P.

For the sketched game it holds that P has a winning strategy iff the formula F ofthe initial claim is indeed valid in G∞. The dialogue rules correspond closely to thelogical rules of an analytic system for G∞, based on so-called sequents of relations,that has been described in [6] and [5].

Moreover we have the following interpretation of O’s moves in the game in termsof (counter) model building:

– Every counter model to F , i.e., every valuation v with v(F) < 1, induces a winningstrategy for O.

– From every winning strategy for O one can extract order constraints that representthe set of all counter models to F .

6 Giles’s game and analytic calculi for fuzzy logics

One of the most remarkable use of Lorenzen style dialogue games in non-classicallogics has been presented by Robin Giles already in the 1970’s. In an attempt toformalize reasoning in physical theories (in particular quantum theory) Giles arrivedat the following game that consists of two largely independent building blocks:

(1) Betting for positive results of experiments. Two players — let’s say me and you,corresponding to P and O, respectively — agree to pay 1 to the opponent player forevery false statement they assert. By [p1, . . . , pm‖q1, . . . ,qn] we denote an elementarystate in the game, where I assert each of the qi in the multiset {q1, . . . ,qn} of atomic


statements (i.e., propositional variables), and you, likewise, assert each atomic state-ment pi ∈ {p1, . . . , pm}.

Each propositional variable q refers to an experiment Eq with binary (yes/no)result. The statement q can be read as ‘Eq yields a positive result’. Things get in-teresting as the experiments may show dispersion; i.e., the same experiment mayyield different results when repeated. However, the results are not completely arbi-trary: for every run of the game, a fixed risk value 〈q〉r ∈ [0,1] is associated with q,denoting the probability that Eq yields a negative result. For the special atomic for-mula ⊥ (falsum) we define 〈⊥〉r = 1. The risk associated with a multiset {p1, . . . , pm}of atomic formulas is defined as 〈p1, . . . , pm〉

r = ∑mi=1〈pi〉

r. The risk 〈〉r associatedwith the empty multiset is defined as 0. The risk associated with an elementary state[p1, . . . , pm‖q1, . . . ,qn] is calculated from my point of view. Therefore the condition〈p1, . . . , pm〉

r ≥ 〈q1, . . . ,qn〉r expresses that I do not expect any loss (but possibly some

gain) when betting on the truth of atomic statements, as explained above.

(2) A dialogue game for the reduction of compound formulas. Giles followsLorenzen in constraining the meaning of connectives by reference to rules of a di-alogue game that proceeds by systematically reducing arguments about compoundformulas to arguments about their subformulas. However he uses a symmetric ver-sion of the game that characterizes classical logic, if the rules for atoms are as inLorenzen’s game for intuitionistic logic.

For brevity, we will assume that formulas are built up from propositional vari-ables, the falsity constant ⊥, and the connective ⊃ only. The central dialogue rule canbe stated as follows:

(R) If I assert A⊃B then, whenever you choose to attack this statement by asserting A,I have to assert also B. (And vice versa, i.e., for the roles of me and you switched.)

This rule reflects the idea that the meaning of implication is specified by the principlethat an assertion of ‘if A, then B’ (A ⊃ B) obliges one to assert also B, if A is granted.

In contrast to dialogue games for intuitionistic logic [25, 14, 24, 18], no specialregulations on the succession of moves in a dialogue are required here. However, weassume that each assertion is attacked at most once: this is reflected by the removalof A ⊃ B from the multiset of all formulas asserted by a player during a run of thegame, as soon as the other player has either attacked by asserting A, or has indicatedthat she will not attack A ⊃ B at all. Consequently every run of the dialogue gameends in an elementary state [p1, . . . , pm‖q1, . . . ,qn]. Given an assignment 〈·〉r of riskvalues to all pi and qi we say that I win the game if I do not expect any loss, i.e., if〈p1, . . . , pm〉

r ≥ 〈q1, . . . ,qn〉r.

Giles proved that the sketched game characterizes the infinitely valuedŁukasiewicz logic Ł in the following sense:


– Every assignment 〈·〉r of risk values to atomic formulas occurring in a formula Finduces a valuation v〈·〉r for Łukasiewicz logic Ł such that v〈·〉r(F) = 1 iff I have awinning strategy for F in the game presented above.

It follows that F is valid in Ł iff, for all assignments of risk values to atomic formulasoccurring in F , I have a winning strategy for F .

We show that an appropriate formalization of generic winning strategies in Giles’sgame corresponds closely to the (analytic) hypersequent system HŁ introduced byMetcalfe, Olivetti, and Gabbay in [26].

Nowadays Łukasiewicz logic is recognized as one of three fundamental t-normbased fuzzy logics, the other two being G∞ (see Sections 3 and 5) and Product logic P

(see, e.g., [21]). In the final part of the tutorial we indicate how the correspondence be-tween Giles’s game and system HŁ can be generalized to include also G∞ and P. Forthis we refer to the recently introduced analytic system rH of Ciabattoni, Fermuller,and Metcalfe [9] that provides a uniform treatment of Ł, G∞, and P. On the side ofthe game, alternatives to Giles’s betting scheme (as explained in (1), above) have tobe considered for the calculation of expected gains/losses of the two players.

7 Final remark

To further assist tutorial participants and interested readers we have made a numberof relevant papers, that have been (co-)authored by C.G. Fermuller available athttp://www.logic.at/people/chrisf/selected.html .

References

1. S. Abramsky, R. Jagadeesan: Games and Full Completeness for Multiplicative Linear Logic. J. SymbolicLogic, 59(2) (1994), 543–574.

2. A. Blass: A Game Semantics for Linear Logic. Annals of Pure and Applied Logic, 56(1992), 183–220.3. A. Blass: Is Game Semantics Necessary? In: Computer Science Logic – 7th Workshop, CSL ’93, Selected

Papers, Springer LNCS 832, 1994, 66–77.4. A. Avron; Hypersequents, logical consequence and intermediate logics for concurrency. Annals of Mathe-

matics and Artificial Intelligence, 4(1991), 225-248.5. M. Baaz, A. Ciabattoni, and C.G. Fermuller: Sequents of Relations Calculi: A Framework for Analytic

Deduction in Many-Valued Logics. In Beyond Two: Theory and Applications of Multiple-Valued Logic, eds:Melvin Fitting and Ewa Orlowska. Studies in Fuzziness and Soft Computing, Physica-Verlag, 2002, 157–180.

6. M. Baaz and C. Fermuller. Analytic calculi for projective logics. In Automated Reasoning with Tableaux andRelated Methods (Tableaux’99), Springer, LNAI 1617, 1999, 36–51.

7. M.P. Bonacina: A taxonomy of parallel strategies for deduction, Annals of Mathematics and Artificial Intel-ligence 29(1–4), 223–257, 2000.

8. M.P. Bonacina, J. Hsiang: On the modelling of search in theorem proving – Towards a theory of strategyanalysis, Information and Computation 147, 171–208, 1998

9. A. Ciabattoni, C.G. Fermuller, G. Metcalfe: Uniform Rules and Dialogue Games for Fuzzy Logics. To appearin Logic for Programming, Artificial Intelligence, and Reasoning, LPAR 2004, Springer LNAI 3452 (2005),496-510.

10. A. Ciabattoni, M. Ferrari. Hypersequent calculi for some intermediate logics with bounded Kripke models.Journal of Logic and Computation, 2(11), pp. 283-294, 2001.


11. A. Ciabattoni, D.M. Gabbay, N. Olivetti. Cut-free proof systems for logics of weak excluded middle. SoftComputing, 2(4), pp 147-156, 1998.

12. M. Dummett. A propositional calculus with denumerable matrix. J. Symbolic Logic, 24(1959), 97–106.13. J.M. Dunn, R.K. Meyer. Algebraic completeness results for Dummett’s LC and its extensions. Z. Math. Logik

Grundlagen Math., 17 (1971), 225–230.14. W. Felscher: Dialogues, Strategies, and Intuitionistic Provability. Annals of Pure and Applied Logic,

28(1985), 217–254.15. W. Felscher: Dialogues as Foundation for Intuitionistic Logic. In: D. Gabbay and F. Gunther (eds.), Handbook

of Philosophical Logic, III, Reidel, 1986, 341–372.16. C.G. Fermuller, A. Ciabattoni. From Intuitionistic Logic to Godel-Dummett Logic via Parallel Dialogue

Games. 33rd Intl. Symp. on Multiple-Valued Logic, Tokyo May 2003, IEEE Press, 188–193.17. C.G. Fermuller: Dialogue Games for Modelling Proof Search in Nonclassical Logics. In: I. Dahn, L. Vigneron

(eds.), FTP’2003, International Workshop on First-Order Theorem Proving, proceedings, Technical ReportDISC-II/10/03, Universidad de Politecnica de Valencia.

18. C.G. Fermuller: Parallel dialogue games and hypersequents for intermediate logics. TABLEAUX 2003,Rome, Italy, LNCS 2796, 48–64.

19. C.G. Fermuller and N. Preining. A dialogue game for intuitionistic fuzzy logic based on comparison ofdegrees of truth. In Proceedings of InTech’03, 2003.

20. K. Godel: Zum intuitionistischen Aussagenkalkul. Anz. Akad. Wiss. Wien, 69(1932), 65-66.21. P. Hajek: Metamathematics of Fuzzy Logic. Kluwer, 1998.22. V. Jankov. The calculus of the weak “law of excluded middle”. Mathematics of the USSR 8, pp. 648–658,

1968.23. E.C.W. Krabbe: Formal Systems of Dialogue Rules. Synthese, 63(1985), 295–328.24. E.C.W. Krabbe: Dialogue Sequents and Quick Proofs of Completeness. In: J.Ph. Hoepelman (ed.), Represen-

tation and Reasoning. Max Niemeyer Verlag, 1988, 135–140.25. P. Lorenzen: Logik und Agon. In: Atti Congr. Internat. di Filosofia, Vol. 4 (Sansoni, Firenze, 1960), 187–194.26. G. Metcalfe, N. Olivetti, and D. Gabbay: Sequent and hypersequent calculi for abelian and Łukasiewicz

logics. To appear in ACM TOCL, 2005.27. S. Rahman: Uber Dialoge, Protologische Kategorien und andere Seltenheiten. Europaische

Hochschulschriften, Peter Lang, 1993.28. N. Shankar: Proof Search in the Intuitionistic Sequent Calculus. Proceedings 11th Intl. Conf. on Automated

Deduction, CADE’92, LNCS 607, Springer, 1992.

Tutorial on Agda

Marcin Benke

Computer Science Department

Chalmers University of Technology, Gothenburg

[email protected]

Tutorial on Agda Structured Type Theory is a logical framework in which we

can express both programs and proofs. It extends Martin-Lof’s type theory by

adding modern programming constructs such as local definitions, modules and

structures. These additions help to structure the proofs better, as well as a better

re-use of code.

The framework is actually a programming language with a strong type sys-

tem, but also unbounded recursion. A proof in this system is correct if it is type

correct, and if it is guaranteed to terminate.

Agda is a type checker and an interpreter for Structured Type Theory, but

not only. It has also commands for developing proofs such as filling in holes,

checking termination, asking for information, pretty printing etc.

On top of Agda we have two interfaces, one emacs-based interface that we

will be used in the tutorial. The other interface, Alfa, is a graphical interface,

which provides syntax directed, direct manipulation of proofs and programs.

The tutorial will cover basics of the type theory, proof construction and

interaction with Agda, as well as combining interactive and automated proofs.

54 Marcin Benke

Author Index

Baumgartner, Peter, 41

Benke, Marcin, 53

Fermuller, Christian G., 43

Formisano, Andrea, 1

Giordano, Laura, 11

Gliozzi, Valentina, 11

Olivetti, Nicola, 11

Omodeo, Eugenio G., 1

Or lowska, Ewa, 1

Pozzato, Gian Luca, 11

Shilov, Nikolay V., 27

Stenz, Gernot, 41

Available Research Reports (since 2000):

2005

12/2005 Bernhard Beckert.TABLEAUX 2005 —Position Papers and Tutorial Descriptions.

11/2005 Dietrich Paulus, Detlev Droege.Mixed-reality as a challenge to imageunderstanding and artificial intelligence.

10/2005 Jurgen Sauer.19. Workshop Planen,Scheduling und Konfigurieren / Entwerfen.

9/2005 Pascal Hitzler, Carsten Lutz, Gerd Stumme.Foundational Aspects of Ontologies.

8/2005 Joachim Baumeister, Dietmar Seipel.Knowledge Engineering and SoftwareEngineering.

7/2005 Benno Stein, Sven Meier zu Eißen.Proceedings of the Second InternationalWorkshop on Text-Based InformationRetrieval.

6/2005 Andreas Winter, Jurgen Ebert.Metamodel-driven Service Interoperability.

5/2005 Joschka Boedecker, Norbert Michael Mayer,Masaki Ogino, Rodrigo da Silva Guerra,Masaaki Kikuchi, Minoru Asada.Gettingcloser: How Simulation and Humanoid Leaguecan benefit from each other.

4/2005 Torsten Gipp, Jurgen Ebert.Web Engineeringdoes profit from a Functional Approach.

3/2005 Oliver Obst, Anita Maas, Joschka Boedecker.HTN Planning for Flexible Coordination OfMultiagent Team Behavior.

2/2005 Andreas von Hessling, Thomas Kleemann,Alex Sinner.Semantic User Profiles and theirApplications in a Mobile Environment.

1/2005 Heni Ben Amor, Achim Rettinger.IntelligentExploration for Genetic Algorithms – UsingSelf-Organizing Maps in EvolutionaryComputation.

2004

12/2004 Manfred Rosendahl.ObjektorientierteImplementierung einer Constraint basiertengeometrischen Modellierung.

11/2004 Urs Kuhlmann, Harry Sneed, AndreasWinter.Workshop Reengineering Prozesse(RePro 2004) — Fallstudien, Methoden,Vorgehen, Werkzeuge.

10/2004 Bernhard Beckert, Gerd Beuster.FormalSpecification of Security-relevant Properties ofUser-Interfaces.

9/2004 Bernhard Beckert, Martin Giese, ElmarHabermalz, Reiner Hahnle, Andreas Roth,Philipp Rummer, Steffen Schlager.Taclets: ANew Paradigm for Constructing InteractiveTheorem Provers.

8/2004 Achim Rettinger.Learning from RecordedGames: A Scoring Policy for Simulated SoccerAgents.

7/2004 Oliver Obst, Markus Rollmann.Spark — AGeneric Simulator for Physical Multi-agentSimulations.

6/2004 Frank Dylla, Alexander Ferrein, GerhardLakemeyer, Jan Murray, Oliver Obst, ThomasRofer, Frieder Stolzenburg, Ubbo Visser,Thomas Wagner.Towards aLeague-Independent Qualitative Soccer Theoryfor RoboCup.

5/2004 Peter Baumgartner, Ulrich Furbach, MargretGroß-Hardt, Thomas Kleemann.Model BasedDeduction for Database Schema Reasoning.

4/2004 Lutz Priese.A Note on Recognizable Sets ofUnranked and Unordered Trees.

3/2004 Lutz Priese.Petri Net DAG Languages andRegular Tree Languages with Synchronization.

2/2004 Ulrich Furbach, Margret Groß-Hardt, BerndThomas, Tobias Weller, Alexander Wolf.IssuesManagement: Erkennen und Beherrschen vonkommunikativen Risiken und Chancen.

1/2004 Andreas Winter, Carlo Simon.ExchangingBusiness Process Models with GXL.

2003

18/2003 Kurt Lautenbach.Duality of MarkedPlace/Transition Nets.

17/2003 Frieder Stolzenburg, Jan Murray, KarstenSturm.Multiagent Matching Algorithms Withand Without Coach.

16/2003 Peter Baumgartner, Paul A. Cairns, MichaelKohlhase, Erica Melis (Eds.).KnowledgeRepresentation and Automated Reasoning forE-Learning Systems.

15/2003 Peter Baumgartner, Ulrich Furbach, MargretGross-Hardt, Thomas Kleemann, ChristophWernhard.KRHyper Inside — Model BasedDeduction in Applications.

14/2003 Christoph Wernhard.System Description:KRHyper.

13/2003 Peter Baumgartner, Ulrich Furbach, MargretGross-Hardt, Alex Sinner.’Living Book’ :-’Deduction’, ’Slicing’, ’Interaction’..

12/2003 Heni Ben Amor, Oliver Obst, Jan Murray.Fast, Neat and Under Control: Inverse SteeringBehaviors for Physical Autonomous Agents.

11/2003 Gerd Beuster, Thomas Kleemann, BerndThomas.MIA - A Multi-Agent Location BasedInformation Systems for Mobile Users in 3GNetworks.

10/2003 Gerd Beuster, Ulrich Furbach, MargretGroß-Hardt, Bernd Thomas.AutomaticClassification for the Identification ofRelationships in a Metadata Repository.

9/2003 Nicholas Kushmerick, Bernd Thomas.Adaptive information extraction: Coretechnologies for information agents.

8/2003 Bernd Thomas.Bottom-Up Learning of LogicPrograms for Information Extraction fromHypertext Documents.

7/2003 Ulrich Furbach.AI - A Multiple BookReview.

6/2003 Peter Baumgartner, Ulrich Furbach, MargretGroß-Hardt.Living Books.

5/2003 Oliver Obst.Using Model-Based Diagnosis toBuild Hypotheses about Spatial Environments.

4/2003 Daniel Lohmann, Jurgen Ebert.AGeneralization of the Hyperspace ApproachUsing Meta-Models.

3/2003 Marco Kogler, Oliver Obst.SimulationLeague: The Next Generation.

2/2003 Peter Baumgartner, Margret Groß-Hardt, AlexSinner.Living Book – Deduction, Slicing andInteraction.

1/2003 Peter Baumgartner, Cesare Tinelli.The ModelEvolution Calculus.

2002

12/2002 Kurt Lautenbach.Logical Reasoning andPetri Nets.

11/2002 Margret Groß-Hardt.Processing of ConceptBased Queries for XML Data.

10/2002 Hanno Binder, Jerome Diebold, TobiasFeldmann, Andreas Kern, David Polock,Dennis Reif, Stephan Schmidt, Frank Schmitt,Dieter Zobel.Fahrassistenzsystem zurUnterstutzung beim R¨uckwartsfahren miteinachsigen Gespannen.

9/2002 Jurgen Ebert, Bernt Kullbach, Franz Lehner.4. Workshop Software Reengineering (BadHonnef, 29./30. April 2002).

8/2002 Richard C. Holt, Andreas Winter, Jingwei Wu.Towards a Common Query Language forReverse Engineering.

7/2002 Jurgen Ebert, Bernt Kullbach, Volker Riediger,Andreas Winter.GUPRO – GenericUnderstanding of Programs, An Overview.

6/2002 Margret Groß-Hardt.Concept based queryingof semistructured data.

5/2002 Anna Simon, Marianne Valerius.UserRequirements – Lessons Learned from aComputer Science Course.

4/2002 Frieder Stolzenburg, Oliver Obst, Jan Murray.Qualitative Velocity and Ball Interception.

3/2002 Peter Baumgartner.A First-Order LogicDavis-Putnam-Logemann-Loveland Procedure.

2/2002 Peter Baumgartner, Ulrich Furbach.Automated Deduction Techniques for theManagement of Personalized Documents.

1/2002 Jurgen Ebert, Bernt Kullbach, Franz Lehner.3. Workshop Software Reengineering (BadHonnef, 10./11. Mai 2001).

2001

13/2001 Annette Pook.Schlussbericht “FUN -Funkunterrichtsnetzwerk”.

12/2001 Toshiaki Arai, Frieder Stolzenburg.Multiagent Systems Specification by UMLStatecharts Aiming at IntelligentManufacturing.

11/2001 Kurt Lautenbach.Reproducibility of theEmpty Marking.

10/2001 Jan Murray.Specifying Agents with UML inRobotic Soccer.

9/2001 Andreas Winter.Exchanging Graphs withGXL.

8/2001 Marianne Valerius, Anna Simon.Slicing BookTechnology — eine neue Technik f¨ur eine neueLehre?.

7/2001 Bernt Kullbach, Volker Riediger.Folding: AnApproach to Enable Program Understanding ofPreprocessed Languages.

6/2001 Frieder Stolzenburg.From the Specification ofMultiagent Systems by Statecharts to theirFormal Analysis by Model Checking.

5/2001 Oliver Obst.Specifying Rational Agents withStatecharts and Utility Functions.

4/2001 Torsten Gipp, Jurgen Ebert.ConceptualModelling and Web Site Generation usingGraph Technology.

3/2001 Carlos I. Chesnevar, Jurgen Dix, FriederStolzenburg, Guillermo R. Simari.RelatingDefeasible and Normal Logic Programmingthrough Transformation Properties.

2/2001 Carola Lange, Harry M. Sneed, AndreasWinter.Applying GUPRO to GEOS – A CaseStudy.

1/2001 Pascal von Hutten, Stephan Philippi.Modelling a concurrent ray-tracing algorithmusing object-oriented Petri-Nets.

2000

8/2000 Jurgen Ebert, Bernt Kullbach,Franz Lehner (Hrsg.).2. Workshop SoftwareReengineering (Bad Honnef, 11./12. Mai2000).

7/2000 Stephan Philippi.AWPN 2000 - 7. WorkshopAlgorithmen und Werkzeuge f¨ur Petrinetze,Koblenz, 02.-03. Oktober 2000 .

6/2000 Jan Murray, Oliver Obst, Frieder Stolzenburg.Towards a Logical Approach for Soccer AgentsEngineering.

5/2000 Peter Baumgartner, Hantao Zhang (Eds.).FTP 2000 – Third International Workshop onFirst-Order Theorem Proving, St Andrews,Scotland, July 2000.

4/2000 Frieder Stolzenburg, Alejandro J. Garcıa,Carlos I. Chesnevar, Guillermo R. Simari.Introducing Generalized Specificity in LogicProgramming.

3/2000 Ingar Uhe, Manfred Rosendahl.Specificationof Symbols and Implementation of TheirConstraints in JKogge.

2/2000 Peter Baumgartner, Fabio Massacci.TheTaming of the (X)OR.

1/2000 Richard C. Holt, Andreas Winter, Andy Schurr.GXL: Towards a Standard Exchange Format.

Fachberichte INFORMATIK - Landau · edged inferential apparatus, where the inferential activity is...

Documents

Transcript of Fachberichte INFORMATIK - Landau · edged inferential apparatus, where the inferential activity is...