Divide and Conquer - McGill...
Transcript of Divide and Conquer - McGill...

1
Chapter 5 Divide and Conquer
Slides by Kevin Wayne. Copyright © 2005 Pearson-Addison Wesley. All rights reserved.
CLRS 4.3

2
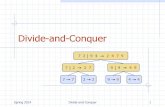
Divide-and-Conquer
Divide-and-conquer. ■ Break up problem into several parts. ■ Solve each part recursively. ■ Combine solutions to sub-problems into overall solution.
Most common usage. ■ Break up problem of size n into two equal parts of size ½n. ■ Solve two parts recursively. ■ Combine two solutions into overall solution in linear time.
Consequence. ■ Brute force: n2. ■ Divide-and-conquer: n log n. Divide et impera.
Veni, vidi, vici. - Julius Caesar

5.1 Mergesort

Sorting. Given n elements, rearrange in ascending order.
4
Obvious sorting applications. List files in a directory. Organize an MP3 library. List names in a phone book. Display Google PageRank results.
Problems become easier once sorted. Find the median. Find the closest pair. Binary search in a database. Identify statistical outliers. Find duplicates in a mailing list.
Non-obvious sorting applications. Data compression. Computer graphics. Interval scheduling. Computational biology. Minimum spanning tree. Supply chain management. Simulate a system of particles. Book recommendations on Amazon. Load balancing on a parallel computer.. . .
Sorting

5
Mergesort
Mergesort. ■ Divide array into two halves. ■ Recursively sort each half. ■ Merge two halves to make sorted whole.
merge
sort
divide
A L G O R I T H M S
A L G O R I T H M S
A G L O R H I M S T
A G H I L M O R S T
Jon von Neumann (1945)
O(n)
2T(n/2)
O(1)

6
Merging
Merging. Combine two pre-sorted lists into a sorted whole.
How to merge efficiently? ■ Linear number of comparisons. ■ Use temporary array.
Challenge for the bored. In-place merge. [Kronrod, 1969]
A G L O R H I M S T
A G H I
using only a constant amount of extra storage

7
auxiliary array
smallest smallest
A G L O R H I M S T
Merge. ■ Keep track of smallest element in each sorted half. ■ Insert smallest of two elements into auxiliary array. ■ Repeat until done.
A
Merging

8
auxiliary array
smallest smallest
A G L O R H I M S T
A
Merge. ■ Keep track of smallest element in each sorted half. ■ Insert smallest of two elements into auxiliary array. ■ Repeat until done.
G
Merging

9
auxiliary array
smallest smallest
A G L O R H I M S T
A G
Merge. ■ Keep track of smallest element in each sorted half. ■ Insert smallest of two elements into auxiliary array. ■ Repeat until done.
H
Merging

10
auxiliary array
smallest smallest
A G L O R H I M S T
A G H
Merge. ■ Keep track of smallest element in each sorted half. ■ Insert smallest of two elements into auxiliary array. ■ Repeat until done.
I
Merging

11
auxiliary array
smallest smallest
A G L O R H I M S T
A G H I
Merge. ■ Keep track of smallest element in each sorted half. ■ Insert smallest of two elements into auxiliary array. ■ Repeat until done.
L
Merging

12
auxiliary array
smallest smallest
A G L O R H I M S T
A G H I L
Merge. ■ Keep track of smallest element in each sorted half. ■ Insert smallest of two elements into auxiliary array. ■ Repeat until done.
M
Merging

13
auxiliary array
smallest smallest
A G L O R H I M S T
A G H I L M
Merge. ■ Keep track of smallest element in each sorted half. ■ Insert smallest of two elements into auxiliary array. ■ Repeat until done.
O
Merging

14
auxiliary array
smallest smallest
A G L O R H I M S T
A G H I L M O
Merge. ■ Keep track of smallest element in each sorted half. ■ Insert smallest of two elements into auxiliary array. ■ Repeat until done.
R
Merging

15
auxiliary array
first half exhausted smallest
A G L O R H I M S T
A G H I L M O R
Merge. ■ Keep track of smallest element in each sorted half. ■ Insert smallest of two elements into auxiliary array. ■ Repeat until done.
S
Merging

16
auxiliary array
first half exhausted smallest
A G L O R H I M S T
A G H I L M O R S
Merge. ■ Keep track of smallest element in each sorted half. ■ Insert smallest of two elements into auxiliary array. ■ Repeat until done.
T
Merging

17
auxiliary array
first half exhausted
second halfexhausted
A G L O R H I M S T
A G H I L M O R S T
Merge. ■ Keep track of smallest element in each sorted half. ■ Insert smallest of two elements into auxiliary array. ■ Repeat until done.
Merging

Def. T(n) = number of comparisons to mergesort an input of size n.
Mergesort recurrence.
Solution. T(n) ∈ O(n log2 n).
Assorted proofs. We describe several ways to prove this recurrence. Initially we assume n is a power of 2 and replace ≤ with =.
18
A Useful Recurrence Relation

19
Proof by Recursion Tree
T(n)
T(n/2)T(n/2)
T(n/4)T(n/4)T(n/4) T(n/4)
T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2)
n
T(n / 2k)
2(n/2)
4(n/4)
2k (n / 2k)
n/2 (2)
. . .
. . .log2n
n log2n

Claim. If T(n) satisfies this recurrence, then T(n) = n log2 n.
Pf. (by induction on n) ■ Base case: n = 1. ■ Inductive hypothesis: T(n) = n log2 n. ■ Goal: show that T(2n) = 2n log2 (2n).
20
Proof by Induction
assumes n is a power of 2

Claim. If T(n) satisfies the following recurrence, then T(n) ≤ n ⎡lg n⎤.
Pf. (by induction on n) ■ Base case: n = 1. T(1) = 0 = 1⎡lg 1⎤. ■ Define n1 = ⎣n / 2⎦ , n2 = ⎡n / 2⎤. ■ Induction step: Let n≥2, assume true for 1, 2, ... , n–1.
21
Analysis of Mergesort Recurrence
log2n

5.5 Integer Multiplication

Add. Given two n-digit integers a and b, compute a + b. ■ Θ(n) bit operations.
1
0
0
1
1
0
1
1
1
0
1
1
1
0
0
1
00000000
01010101
01010101
01010101
01010101
01010101
00000000
0100000000001011
1
0
1
1
1
1
1
0
0
×
Multiply
Multiply. Given two n-digit integers a and b, compute a × b. ■ Straight forward solution: Θ(n2) bit operations.
10101011 0
23
Integer Arithmetic
1
011 1
110 1+
010 1
111
010 1
011 1
100 0
10111
Add

To multiply two n-digit integers: ■ Multiply four ½n-digit integers. ■ Add two ½n-digit integers, and shift to obtain result.
assumes n is a power of 2
24
Divide-and-Conquer Multiplication: Warmup
∈

Claim.
Pf. For n > 1: T(n)/n = 4T(n/2)/n + C = 2 T(n/2)/(n/2) + C = 2 [ 2 T(n/4)/(n/4) + C ] + C = 4 T(n/4)/(n/4) + 2C + C = 4 [ 2 T(n/8)/(n/8) + C ] + 2C + C = 8 T(n/8)/(n/8) + 4C + 2C + C ... = n T(1)/(1) + n/2 C + n/4 C + ... + 4C + 2C + C = C (n/2+n/4+...+2+1) = C(n-1).
25
Proof by Telescoping
assumes n is a power of 2
∈

To multiply two n-digit integers: ■ Add two ½n digit integers. ■ Multiply three ½n-digit integers. ■ Add, subtract, and shift ½n-digit integers to obtain result.
26
Karatsuba Multiplication
Theorem. [Karatsuba-Ofman, 1962] Can multiply two n-digit integers in O(n1.585) bit operations.
∈ ∈

27
Karatsuba: Recursion Tree
n
3(n/2)
9(n/4)
3k (n / 2k)
3 lg n (2)
. . .
. . .
T(n)
T(n/2)
T(n/4) T(n/4)
T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2)
T(n / 2k)
T(n/4)
T(n/2)
T(n/4) T(n/4)T(n/4)
T(n/2)
T(n/4) T(n/4)T(n/4)
. . .
. . .
n

28
Generalization: O(n1+ε) for any ε > 0.
Best known: (n log n) 2O(log* n)
Conjecture: Ω(n log n) but not proven.
Karatsuba Multiplication
0 if x≤1 where log*(x)= 1+log*(log x) if x>1{

CLRS 4.3 Master Theorem

Master Theorem from CLRS 4.3
30
a = (constant) number of sub-instances,b = (constant) size ratio of sub-instances,𝑓(n) = time used for dividing and recombining.
T(n) = aT(n/b) + f(n)

T(n/b2)
. . .T(n / bk)
31
Proof by Recursion Tree
f(n)
af(n/b)
a2 f(n/b2)
ak f(n/bk)
alogb n T(2)
. . .
T(n)
T(n/b)
T(n/b2) T(n/b2)
T(2)
T(n/b2)
T(n/b)
T(n/b2) T(n/b2)T(n/b2)
T(n/b)
T(n/b2) T(n/b2)
T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2)
T(n / bk)
. . .
T(n / bk) T(n / bk) T(n / bk)T(n / bk)T(n / bk)T(n / bk)T(n / bk)
logbn. . .
= T(2) nlogb a
T(n) = ∑ ak f(n/bk)
T(n) = aT(n/b) + f(n)

Solution: T(n) ∈ 𝛩(𝑓(n))
Solution: T(n) ∈ 𝛩(nlogb a)
32
isCase 3: 𝑓(n) ∈ 𝛺(nL) for some constant L > logb aand 𝑓(n) satisfies the regularity condition a𝑓(n/b) ≤ c𝑓(n) for some c<1 and all large n.
Case 1: 𝑓(n) ∈ O(nL) for some constant L < logb a.
Solution: T(n) ∈ 𝛩(nlogb a logk+1 n)
Case 2: 𝑓(n) ∈ 𝛩(nlogb a logk n), for some k ≥ 0.
T(n) = aT(n/b) + f(n)

33
is
Master Theorem
Case 1: 𝑓(n) ∈ O(nL) for some constant L < logb a.
Solution: T(n) ∈ 𝛩(nlogb a)
T(n) = aT(n/b) + f(n)

Solution: T(n) ∈ 𝛩(nlogb a)
34
Master Theorem
Case 1: 𝑓(n) ∈ O(nL) for some constant L < logb a.
T(n) = 5T(n/2) + 𝛩(n2)
Compare nlog2 5 vs. n2.
Since 2 < log2 5 use Case 1
Solution: T(n) ∈ 𝛩(nlog2 5)

35
Master Theorem
Solution: T(n) ∈ 𝛩(nlogb a log n)
Simple Case 2: 𝑓(n) ∈ 𝛩(nlogb a).
T(n) = aT(n/b) + f(n)

36
Master Theorem
Solution: T(n) ∈ 𝛩(nlogb a logk+1 n)
Case 2: 𝑓(n) ∈ 𝛩(nlogb a logk n), for some k ≥ 0.
T(n) = aT(n/b) + f(n)

T(n) = 27T(n/3) + 𝛩(n3 log n)
Compare nlog3 27 vs. n3.
Since 3 = log3 27 use Case 2
Solution: T(n) ∈ 𝛩(n3 log2 n)37
Master Theorem
Solution: T(n) ∈ 𝛩(nlogb a logk+1 n)
Case 2: 𝑓(n) ∈ 𝛩(nlogb a logk n), for some k ≥ 0.

38
Master Theorem
Solution: T(n) ∈ 𝛩(𝑓(n))
Case 3: 𝑓(n) ∈ 𝛺(nL) for some constant L > logb aand 𝑓(n) satisfies the regularity condition a𝑓(n/b) ≤ c𝑓(n) for some c<1 and all large n.
T(n) = aT(n/b) + f(n)

Solution: T(n) ∈ 𝛩(𝑓(n))
Case 3: 𝑓(n) ∈ 𝛺(nL) for some constant L > logb aand 𝑓(n) satisfies the regularity condition a𝑓(n/b) ≤ c𝑓(n) for some c<1 and all large n.
39
∈
Master Theorem

40
Master Theorem
Solution: T(n) ∈ 𝛩(𝑓(n))
Case 3: 𝑓(n) ∈ 𝛺(nL) for some constant L > logb aand 𝑓(n) satisfies the regularity condition a𝑓(n/b) ≤ c𝑓(n) for some c<1 and all large n.
T(n) = 5T(n/2) + 𝛩(n3)
Compare nlog2 5 vs. n3.
Since 3 > log2 5 use Case 3
a𝑓(n/b) = 5(n/2)3 = 5/8 n3 ≤ cn3, for c = 5/8
Solution: T(n) ∈ 𝛩(n3)

41
Master Theorem
T(n) = 27T(n/3) + 𝛩(n3/log n)
Compare nlog3 27 vs. n3.
Since 3 = log3 27 use Case 2
but n3/log n ∈ not 𝛩(n3 log k n) for k ≥ 0
Cannot use Master Method.

Matrix Multiplication

43
Matrix multiplication. Given two n-by-n matrices A and B, compute C = AB.
Brute force. Θ(n3) arithmetic operations.
Fundamental question. Can we improve upon brute force?
Matrix Multiplication

Divide-and-conquer. ■ Divide: partition A and B into ½n-by-½n blocks. ■ Conquer: multiply 8 ½n-by-½n recursively. ■ Combine: add appropriate products using 4 matrix additions.
44
Matrix Multiplication: Warmup
∈

Key idea. multiply 2-by-2 block matrices with only ⑦ multiplications.
■ 7 multiplications. ■ 18 = 10 + 8 additions (or subtractions).
45
Matrix Multiplication: Key Idea

log2n
46
Strassen: Recursion Tree
n2
7(n2/22)
49(n2/42)
7k (n2/ 4k)
7 lg n (n2/ 4 lg n)
=7 lg n = n lg 7
. . .
. . .
T(n)
T(n/2)
T(n/4)
T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2)
T(n / 2k)
T(n/2)
T(n/4) T(n/4)T(n/4)
T(n/2)
T(n/4) T(n/4)T(n/4)
. . .
. . .
T(n/2) T(n/2) T(n/2) T(n/2)
774
74
74
773
T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)
≈ .n2 n2 =n2

47
Fast Matrix Multiplication
Fast matrix multiplication. (Strassen, 1969) ■ Divide: partition A and B into ½n-by-½n blocks. ■ Compute: 14 ½n-by-½n matrices via 10 matrix additions. ■ Conquer: multiply 7 ½n-by-½n matrices recursively. ■ Combine: 7 products into 4 terms using 18 matrix additions.
Analysis. ■ Assume n is a power of 2. ■ T(n) = # arithmetic operations.
∈ ∈

48
Fast Matrix Multiplication in Practice
Implementation issues. ■ Sparsity. ■ Caching effects. ■ Numerical stability. ■ Odd matrix dimensions. ■ Crossover to classical algorithm around n = 128.
Common misperception: "Strassen is only a theoretical curiosity." ■ Advanced Computation Group at Apple Computer reports 8x speedup
on G4 Velocity Engine when n ~ 2,500. ■ Range of instances where it's useful is a subject of controversy.
Remark. Can "Strassenize" Ax=b, determinant, eigenvalues, and other matrix ops.

Q. Two 70-by-70 matrices with only 143,640 scalar multiplications? A. Yes! [Pan, 1980]
49
Fast Matrix Multiplication in Theory
Q. Multiply two 2-by-2 matrices with only 7 scalar multiplications? A. Yes! [Strassen, 1969] Θ
�
� (n log2 7 ) = O(n 2.81)∈
�
� (n log2 6) = O(n 2.59 )Θ ∈
�
� (n log3 21) = O(n 2.77 )Θ ∈
�
� (n log70 143640 ) = O(n 2.80 )Θ ∈
Q. Multiply two 2-by-2 matrices with only 6 scalar multiplications? A. Impossible. [Hopcroft and Kerr, 1971]
Q. Two 3-by-3 matrices with only 21 scalar multiplications? A. Also impossible.
Decimal wars. ■ December, 1979: O(n2.521813). ■ January, 1980: O(n2.521801).

50
Fast Matrix Multiplication in Theory
Best known. O(n2.376) [Coppersmith-Winograd, 1987-2010.]
In 2010, Andrew Stothers gave an improvement to the algorithm O(n2.374). In 2011, Virginia Williams combined a mathematical short-cut from Stothers' paper with her own insights and automated optimization on computers, improving the bound O(n2.3728642). In 2014, François Le Gall simplified the methods of Williams and obtained an improved bound of O(n2.3728639).
Conjecture. O(n2+ε) for any ε > 0.
Caveat. Theoretical improvements to Strassen are progressively less practical (hidden constant gets worse).

5.4 Closest Pair of Points

52
Closest Pair of Points
Closest pair. Given n points in the plane, find a pair with smallest Euclidean distance between them.
Fundamental geometric primitive. ■ Graphics, computer vision, geographic information systems,
molecular modeling, air traffic control. ■ Special case of nearest neighbor, Euclidean MST, Voronoi.
Brute force. Check all pairs of points p and q with Θ(n2) comparisons.
1-D version. O(n log n) easy if points are on a line.
Assumption. No two points have same x coordinate.
to make presentation cleaner
fast closest pair inspired fast algorithms for these problems

53
Algorithm. ■ Divide: draw vertical line L so that roughly ½n points on each side.
L
Closest Pair of Points

54
Algorithm. ■ Divide: draw vertical line L so that roughly ½n points on each side. ■ Conquer: find closest pair in each side recursively.
12
21
L
Closest Pair of Points

55
Algorithm. ■ Divide: draw vertical line L so that roughly ½n points on each side. ■ Conquer: find closest pair in each side recursively. ■ Combine: find closest pair with one point in each side. ■ Return best of 3 solutions.
12
218
L
seems like Θ(n2)
Closest Pair of Points

56
Find closest pair with one point in each side, assuming that distance < δ.
12
21
δ = min(12, 21)
L
Closest Pair of Points

57
Find closest pair with one point in each side, assuming that distance < δ. ■ Observation: only need to consider points within δ of line L.
12
21
δ
L
δ = min(12, 21)
Closest Pair of Points

Find closest pair with one point in each side, assuming that distance < δ. ■ Observation: only need to consider points within δ of line L. ■ Sort points in 2δ-strip by their y coordinate.
58
12
21
1
2
3
45
6
7L
δ = min(12, 21)
δ
Closest Pair of Points

Find closest pair with one point in each side, assuming that distance < δ. ■ Observation: only need to consider points within δ of line L. ■ Sort points in 2δ-strip by their y coordinate. ■ Only check distances of those within 11 positions in sorted list!
59
12
21
1
2
3
45
6
7L
δ = min(12, 21)
δ
Closest Pair of Points

Def. Let si be the point in the 2δ-strip, withthe ith smallest y-coordinate.
Claim. If |i – j| ≥ 12, then the distance betweensi and sj is at least δ. Pf. ■ No two points lie in same ½δ-by-½δ box. ■ Two points at least 2 rows apart
have distance ≥ 2(½δ) = δ. ▪
Fact. Still true if we replace 12 with 7.
60δ
27
2930
31
28
26
25
δ
½δ
2 rows½δ
½δ
39
i
j
Scan points in y-order and compare distance between each point and next 11 neighbours. If any of these distances is less than δ, update δ.
Closest Pair of Points

61
Smallest-Dist(p1, …, pn) {
if n=2 then return dist(p1,p2)
Compute separation line L such that half the points are on one side and half on the other side.
δ’ = Smallest-Dist(left half) δ’’ = Smallest-Dist(right half) δ = min(δ’,δ’’)
Delete all points further than δ from separation line L
Sort remaining points by y-coordinate.
Scan points in y-order and compare distance between each point and next 11 neighbours. If any of these distances is less than δ, update δ.
return δ. }
O(n log n)
2T(n / 2)
O(n)
O(n log n)
O(n)
Closest Pair of Points

62
Closest-Pair(p1, …, pn) {
if n=2 then return dist(p1,p2),p1,p2
Compute separation line L such that half the points are on one side and half on the other side.
δ’,p’,q’ = Closest-Pair(left half) δ’’,p’’,q’’ = Closest-Pair(right half) δ, p, q = min(δ’, δ’’)(p’,q’,p’’,q’’)
Delete all points further than δ from separation line L
Sort remaining points by y-coordinate.
Scan points in y-order and compare distance between each point and next 11 neighbours. If any of these distances is less than δ, update δ,p,q.
return δ,p,q. }
O(n log n)
2T(n / 2)
O(n)
O(n log n)
O(n)
Closest Pair of Points

63
Closest Pair of Points: Analysis
Running time.
Q. Can we achieve O(n log n)?
A. Yes. First sort all points according to x coordinate before algo. Don’t sort points in strip from scratch each time. ■ Each recursion returns a list: all points sorted by y coordinate. ■ Sort by merging two pre-sorted lists.
∈
∈

Beyond the Master Theorem

Median Finding

66
Median Finding. Given n distinct numbers a1, …, an, find i such that
|{ j : aj<ai }| =⎣n-1 / 2⎦ and |{ j : aj>ai }| =⎡n-1 / 2⎤.
Median Finding
22 31 44 7 12 19 20 35 3 40 27
3 7 12 19 20 22 27 31 35 40 44
9 4 5 6 7 1 11 2 8 10 3

67
Selection. Given n distinct numbers a1, …, an, and index k, find i such that
|{ j : aj<ai }| = k-1 and |{ j : aj>ai }| = n-k.
k=4
Selection
22 31 44 7 12 19 20 35 3 40 27
3 7 12 19 20 22 27 31 35 40 44
9 4 5 6 7 1 11 2 8 10 3
Median( a1, …, an ) = Selection( a1, …, an,⎣n+1 / 2⎦)

Algorithm partition(A, start, stop)
Input: An array A, indices start and stop.
Output: Returns an index j and rearranges the elements of Asuch that for all i<j, A[i] ! A[j] andfor all k>i, A[k] " A[j].
pivot # A[stop]
left # start
right # stop - 1
while left ! right do
while left ! right and A[left] ! pivot) do left # left + 1
while (left ! right and A[right] " pivot) do right # right -1
if (left < right ) then exchange A[left] $ A[right]
exchange A[stop] $ A[left]
return left
Partition (from QuickSort)
j<
<(

Example of execution of partition
A = [ 6 3 7 3 2 5 7 5 ] pivot = 5
A = [ 6 3 7 3 2 5 7 5 ] swap 6, 2
A = [ 2 3 7 3 6 5 7 5 ]
A = [ 2 3 7 3 6 5 7 5 ] swap 7,3
A = [ 2 3 3 7 6 5 7 5 ]
A = [ 2 3 3 7 6 5 7 5 ] swap 7,pivot
A = [ 2 3 3 5 6 5 7 7 ]!5 "5
Partition
<

Partition
70
Selection. Given n distinct numbers a1, …, an, and index k, find i such that |{ j : aj<ai }| = k-1 and |{ j : aj>ai }| = n-k.
aj<ai m i aj>ai
k<m k>m
Selection from Median
ai
Median*
↓
Selection( A,start,m-1,k )Selection( A,m+1,stop,k)
if k = m return m
Selection( A,start,stop,k ) (where start ≤ k ≤ stop)
*Median( A,start,stop ) = Selection( A,start,stop,⎡stop-start / 2⎤ )

Partition
71
Selection. Given n distinct numbers a1, …, an, and index k, find i such that |{ j : aj<ai }| = k-1 and |{ j : aj>ai }| = n-k.
aj<ai m i aj>ai
k<m k>m
Selection from Median
ai
↓
Selection( A,start,m-1,k )Selection( A,m+1,stop,k)
if k = m return m
Selection( A,start,stop,k ) (where start ≤ k ≤ stop)
*Median( A,start,stop ) = Selection( A,start,stop,⎡stop-start / 2⎤ )
Median*

Selection. Given n distinct numbers a1, …, an, and index k, find i such that |{ j : aj<ai }| = k-1 and |{ j : aj>ai }| = n-k.
i m aj>ai
k<m k>m
72
Selection from Median
ai
↓
Selection( A,m+1,stop,k)
if k = m return m
Selection( A,start,stop,k ) (where start ≤ k ≤ stop)
*Median( A,start,stop ) = Selection( A,start,stop,⎡stop-start / 2⎤ )
Partition
Selection( A,start,m-1,k )
Median*

73
Select(a1, …, an,k) {
copy a1, …, an into A[1]…A[n] return SelectREC(A,1,n,k)
}
SelectREC(A,start,stop,k) {
if start=stop then return stop
i = Median(A,start,stop) {* = Selection(A,start,stop,⎡stop-start / 2⎤)*} exchange A[i] with A[stop] m = partition(A,start,stop)
if k=m then return m if k<m then return SelectREC(A,start,m-1,k)
else return SelectREC(A,m+1,stop,k). }
Selection from Median

Selection. Given n distinct numbers a1, …, an, and index k, find i such that |{ j : aj<ai }| = k-1 and |{ j : aj>ai }| = n-k.
aj<ai m i aj>ai
ai
74
Selection
Pseudo- Median
↓
k < m Selection( A,start,m-1,k ) k > m
Selection( A,m+1,stop,k )
Partition
if k = m return m
Selection( A,start,stop,k ) (where start ≤ k ≤ stop)

75
Select(a1, …, an,k) {
copy a1, …, an into A[1]…A[n] return SelectREC(A,1,n,k)
}
SelectREC(A,start,stop,k) {
if start=stop then return stop
i = PseudoMedian(A,start,stop) exchange A[i] with A[stop] m = partition(A,start,stop)
if k=m then return m if k<m then return SelectREC(A,start,m-1,k)
else return SelectREC(A,m+1,stop,k). }
Selection from Pseudo-Median

76
PseudoMedian(A,start,stop) {
for i=0 to ⎡stop-start / 5⎤-1 B[i+1] = A[AdHcMed5(A[start+5*i],
A[start+5*i+1], A[start+5*i+2], A[start+5*i+3], A[start+5*i+4]) ]
m = SelectREC(B,1, ⎡stop-start / 5⎤,⎡stop-start / 10⎤) find j such that A[j]=B[m] return j
}
Selection from Pseudo-Median

77 3n/10——————————7n/10
SelectionSelection. Given n distinct numbers a1, …, an, and index k, find i such that |{ j : aj<ai }| = k-1 and |{ j : aj>ai }| = n-k.
SORT

Selection. Given n distinct numbers a1, …, an, and index k, find i such that
|{ j : aj<ai }| = k-1 and |{ j : aj>ai }| = n-k.
T(n) ≤ T(⎡n/5⎤) + Max{ T(⎣3n/10⎦… T(⎡7n/10⎤) } + 𝛩(n)
Solution: T(n) ∈ 𝛩(n)
78
Selection

Selection. Given n distinct numbers a1, …, an, and index k, find i such that
|{ j : aj<ai }| = k-1 and |{ j : aj>ai }| = n-k.
Assuming T(i) ≤ d i for 1 ≤ i ≤ n, 𝛩(n) ≤ cn T(n+1) ≤ T(n+1 /5) + T(7(n+1)/10) + c(n+1) ≤ d(n+1)/5 + 7d(n+1)/10 + c(n+1) = (2d+7d+10c)/10 (n+1) = (9d+10c)/10 (n+1) ≤ d (n+1) as long as (9d+10c)/10 ≤ d, or equivalently 10c ≤ d.
T(n) ≤ T( n/5 ) + T( 7n/10 ) + 𝛩(n) Solution: T(n) ∈ 𝛩(n)
79
Selection

Selection. Given n distinct numbers a1, …, an, and index k, find i such that
|{ j : aj<ai }| = k-1 and |{ j : aj>ai }| = n-k.
example: d=10c, Assuming T(i) ≤ 10c i for 1 ≤ i ≤ n, 𝛩(n) ≤ cn T(n+1) ≤ T(n+1 /5) + T(7/10 (n+1)) + c(n+1) ≤ 10c/5 (n+1) + 7•10c/10 (n+1) + c(n+1) = (2c+7c+c)(n+1) = 10c (n+1)
80
Selection
T(n) ≤ T( n/5 ) + T( 7n/10 ) + 𝛩(n) Solution: T(n) ∈ 𝛩(n)

81
Chapter 5 Divide and Conquer
Slides by Kevin Wayne. Copyright © 2005 Pearson-Addison Wesley. All rights reserved.
CLRS 4.3