Dancing with Mathematics:Exploring the Symmetry of the Body

Karl SchafferDr. Schaffer and Mr. Stern Dance Ensembleand De Anza CollegeMathdance.orgkarl_schaffer@yahoo.comSome materials developed with Erik Stern and Scott Kim

California Math Council NorthAsilomarDec. 1, 2012

MATH

DANCE

Erik SternWeber State Univ.

Scott KimPuzzle Designer

Karl Schaffer

Many of the activities I will present as my part of this workshop were developed by myself and Erik Stern, with some input from Scott Kim. Erik and I have co-directed the Dr. Schaffer and Mr. Stern Dance Ensemble for twenty years, and have created about ten different dance concerts integrating dance and mathematics. This photo is from our 3 person show with Scott, The Secret Life of Squares.

“Symmetry is lifeless.”-Doris Humphrey 1895-1958

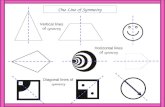
Bilateral symmetry

Facing Orientation

Same Same

Opposite Opposite

Opposite Same

Same Opposite

• Translation (Slide)

• Reflection (Mirror, Flip)

• Rotation ( , Turn)

• Glide (Footsteps)

180

Four symmetry operations acting in a line. We imagine each symmetry transformation acting on one dancer to give the position of a second dancer.Facing indicates whether the dancers are facing the same or opposite directions on the line.Orientation indicates whether the dancers are both gesturing with the right limb (“same”), or one uses the right, the other the left “(opposite”).Translation, when done by a group of dancers is sometimes called shadowing or flocking.

Vocabulary

Translation = SlideReflection = FlipRotation = Turn

Glide = Footsteps

http://nebula2.deanza.edu/~karl/handouts/2012.CMC.North.pdf

or emailkarl_schaffer@yahoo.com

Grade 4 Calif. Geometry Standards:Recognize a line of symmetry for a two-dimensional figure as a line across the figure such that the figure can be folded along the line into matching parts. Identify line-symmetric figures and draw lines of symmetry.

Grade 8 Calif. Algebra Standard:Use the process of factoring and completing the square in a quadratic function to show zeros, extreme values, and symmetry of the graph, and interpret these in terms of a context.

Calif. High School Standards

Function:Use the process of factoring and completing the square in a quadratic function to show zeros, extreme values, and symmetry of the graph, and interpret these in terms of a context.

Trigonometry:Use the unit circle to explain symmetry (odd and even) and periodicity of trigonometric functions.

Geometry:Recognize a line of symmetry for a two-dimensional figure as a line across the figure such that the figure can be folded along the line into matching parts. Identify line-symmetric figures and draw lines of symmetry.

Calif. Practice Standards:7. Look for and make use of structure.Mathematically proficient students look closely to discern a pattern or structure.

Grade 1:Describe, extend, and explain ways to get to a next element in simple repeating patterns (e.g., rhythmic, numeric, color, and shape).

Grade 3:Patterns in arithmetic...

Grade 4:“Generate and analyze patterns.”

Grade 5:“Analyze patterns and relationships.”

Grade 6:Patterns in data...

Transformational Geometry

(1872) Allowed transformations preserve properties and

correspond to symmetries.

Felix Klein1849-1925

Other Dance Symmetries

Symmetries in time: Canon.

Reversals:

Retrograde. Movement performed as if time were reversed.

Inversion. Sequence of movements performed in reverse order.

Symmetries in dance and music also include symmetries in time: one dancer or instrument repeats a phrase a certain number of beats after another. Or the phrase is repeated in the reverse order. The silent film comedian Charlie Chaplin was so adept at body movement that he sometimes acted scenes backwards, then ran the film backwards so the movement looked correct. This enabled him to safely perform stunts like having a car screech to a halt just in time to not hit him. It is extremely difficult to walk backwards so it looks normal when reversed in time. This is a kinesthetic example of “the negative of a negative is a positive!” In what other films or videos has this trick been used? (One is the barroom scene in John Sayles’ Brother From Another Planet.)

Opposition: the resemblance in walking between the arms and

legs: “helical symmetry.”

www.nordicwalker.com

Other symmetries apparent in dance, gymnastics, sports,... or just walking!

Front/back silhouette

Other symmetries in dance include those derived from the similarity between the human body’s silhouette as seen from the front and the back.

www.jupiterimages.com

Momix

Resemblance in shape and motion between the arms and

the legs in a cartwheel (reflection in the horizontal or “transverse” plane - or also in the “sagittal”

front-to-back plane).

If arms are raised in opposition to legs, there may be a “central inversion.” Or choreography can make use of the resemblance in shape and motion between the arms and the legs, as in a cartwheel.

(2,3)

(2,–3)

(–2,3)

(–2,–3)Reflection in x-axis

Reflection in y-axis

180 degree rotation(or reflection in x-axis and y-axis)

The Klein four group in elementary algebra.

(2,3)

(2,–3)

(–2,3)

(–2,–3)

(–3,–2) (3,–2)

(3,2)

(–3,–2)(–3,–2)

(–3,2)

Reflect in line y = xor line y = –x

When we add in reflection through the line y=x, we get the dihedral group D4, the symmetries of the square.

Eight Square DancersDihedral group D4 of order 8

1 2

34

Quarter turn

See similar analyses of Contra dance by Bernie Scanlon and Larry Copes.(Other transformations are also commonly used in these dance forms.)

- 3 -2 -1 1 2 3

-3

-2

-1

1

2

3„x

- 3 -2 -1 1 2 3

-3

-2

-1

1

2

3- „x

- 3 -2 -1 1 2 3

-3

-2

-1

1

2

3„- x

- 3 -2 -1 1 2 3

-3

-2

-1

1

2

3- „- x

y = ex y = e– x

–y = ex –y = e– x

- 3 -2 -1 1 2 3

-3

-2

-1

1

2

3„x

y = ex

- 3 -2 -1 1 2 3

-3

-2

-1

1

2

3logHxL

x = ey

ory = ln x

Silicon DioxideSymmetry example: chemistry

Sand, quartz - used in glass, semiconductors, petroleum products, timekeeping.

Which symmetries do you see?

Islamic tilings

The AlhambraGrenada, Spain

1238 ADIts walls are covered with tesselations,or tilings, like those that inspired Escher

An example of ethnomathematics is the recent attention to the mathematics of tilings or tesselations, present in visual and fabric arts in a variety of cultures, but reaching a zenith in Islamic arts or 700 years ago.Alhambra construction began in 1238 with construction of a palatial city by Moorish artisans.

M.C. Escher, 1898-1972

Studied at the Alhambra, 1936;Interacted with mathematician Coxeter

Abu’l Wafa940-998 AD

Persian mathematician who wrote a book about discussions between

tiling artisans and mathematicians of his time.

Abu’l Wafa was an astronomer/mathematician who documented, interacted with, and contributed to the knowledge of the artists creating the tilings of the tim.

M.C. Escher began his tiling work after studying the tilings of the Alhambra. As did the ancient artisans, he also interacted with mathematicians of his time.

Quasicrystalxray diffraction pattern of alloys

with crystal-like properties

http://www.lassp.cornell.edu/lifshitz/

Penrose tilingRoger Penrose, physicist, 1974

Would produce an xray diffraction patternlike that on the right.

Aluminum alloy D. Schechtman, 1984

Recent attention in mathematics has focused on Penrose tilings, which arose in the field of “recreational mathematics,” but were later seen to have connections to actual and previously unsuspected structures found in nature.Prior to the discovery of quasicrystals, it was thought that crystalline structures could not have five- or ten-fold symmetries. There is much current research on the properties - and uses - of these alloys.

DeifiedRotatorWas it a rat I saw? Able was I ere I saw ElbaA man, a plan, a canal, Panama!A man, a plan, a cat, a ham, a yak, a yam, a hat, a

canal, Panama!Madam, in Eden I'm Adam,Fall leaves after leaves fall.So patient a doctor, to doctor a patient so.Ominous cinemaWe revere you

Palindromes

T G M RT

G

M GR

Firstsymmetry

Second symmetry

p q b p bMirror Rotate Glide

Translation

Glide

Mirror

Rotation

Rot

atio

n

Tran

slat

ion

Glid

e

Mirr

orgives

Building the composition table for these four transformations.

The “Klein four symmetry group”(or the credit card or mattress rotation group!)

T G M R

G T R M

M R T G

R M G T

T G M R

T

G

M

R

Translation

Glide

Mirror

180 Rotation°

The resulting table. In classes we ask students to find patterns in the table, and see if they can explain what those patterns mean in terms of dancers moving in space. Patterns are usually actually theorems about finite groups.

0 1 2 3

0

1

2

3

Firstturn

Second turn

Quarter Turn table

The cyclic group Z4 is easily modeled with quarter turns.

0 1 2 3

0 0 1 2 3

1 1 2 3 0

2 2 3 0 1

3 3 0 1 2

Firstturn

Second turn

Quarter Turn table

The cyclic group Z4 is easily modeled with quarter turns.

1 i –1 – i

i0 = 1 1 i –1 – i

i1 = i i –1 – i 1

i2 = –1 –1 – i 1 i

i3 = – i – i 1 i –1

−1Powers of i =

i represents quarter turns

The “turn table” is the same group as that of the four fourth roots of one. Imaginary numbers are no more “imaginary” than turning as we move through space.

1 i –1 –ii –1 –i 1–1 –i 1 i–i 1 i –1

17 Wallpaper Groups(Wolfram.com)

pLeader

p4m (*442): Two rotation centers of order 4, one of order 2,4 perp. & diagonal reflections, glide between reflections

p bdqTranslation Reflection Rotation Glidep

b

bqd

p

b q q

bbq

dp

b q q

b

bqd

p

b q q

b

bqd

pb q q

M.C. Escher1898-1972

Tessellation:No gaps

No overlaps

The Alhambra

Pentagons?

Marjorie Rice

Mitsubishi Hupcaps

Which have mirror symmetries?

Which have rotational symmetries?

Mitsubishi Hupcaps

Which have mirror symmetries?

Which have rotational symmetries?

Detailed symmetry activities in our bookMath Dance

http://mathdance.org/html/store.html

Extra slides

Bilateral symmetry

Mirror

(opposite directions)

Translation(same

direction)

Rotation(opposite directions)

Glide(same

direction)

face to side

face to side

face each other

face same way

How a pair of dancers may smoothly sequence through all four of the symmetries. Each change requires the dancers to both move to positions of bilateral symmetry within their own bodies.

A B

CD

A

A

A

B

B

B

C

C

C

D

D

D

ABCD –>BADC

ABCD –>DCBA

ABCD –>CDAB

I

Mx: Reflect in yz-plane (or switch x and –x)My(x,y,z) = (x,–y,z)Mz (x,y,z) = (x,y,–z)

Rx(x): Rotate 180 degrees around x-axis Ry(x,y,z) = (–x,y,–z)Rz (x,y,z) = (–x,–y,z)

Inversion(x,y,z) = (–x,–y,–z)

y

z

x

My Mx

Mz

Rz

Rx Ry MxRx, MyRy, MzRzRxMx, RyMy, RzMz

I

IPoint Inversion

Mult. 1 i j k –1 –i –j –k

1 1 i j k

i i –1 k –j

j j –k –1 i

k k j –i –1

–1

–i

–j

–k

Quaternions

- 3 -2 -1 1 2 3

-3

-2

-1

1

2

3logHxL

- 3 -2 -1 1 2 3

-3

-2

-1

1

2

3logH- xL

- 3 -2 -1 1 2 3

-3

-2

-1

1

2

3- logHxL

- 3 -2 -1 1 2 3

-3

-2

-1

1

2

3- logH- xL

± ln(± x)

- 3 -2 -1 1 2 3

-3

-2

-1

1

2

3

± e(± x) and ± ln(± x)

Functions +/– f(+/–x) and their inverses: another model of these groups.