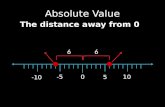
Absolute Value

The absolute value of any number nis its distance from zero on a number line and is written as |n|.

1. If |x| = n, then x = -n AND x = n

This is true because the symbol |x| means x is the distance of n away from zero, both in the

positive direction and in the negative direction.

1. If |x| <n, then x<n and x> -n.

This is true because if x is the distance of n away from zero, this is an AND inequality that was studied in the last section. In other words, x

is all the possible numbers in between –nand n.

3. If |x| >n, then x>n and x< -n.

This is true because if x is n distance away from x, then x would be outside of –n and n on the

number line.