15. Multiple Regression

• How do we actually request the regressions in SPSS?

• How do we use regression to explicate a bivariate relationship with a third variable?

• What do we look for once we have run the relevant regressions?

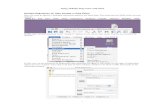
To use a single independent variable, family size, to predict the number of credit cards in a family, we first choose 'Regression | Linear...' from the Analyze menu.

For this analysis, we accept all of the other defaults specified by SPSS. Fourth, click on the OK button to produce the output.

Second, in the 'Linear Regression' dialog box, move the variable 'Number of Credit Cards (ncards)' to the 'Dependent: ' variable list.

Third, move the variable 'Family Size (famsize)' to the 'Independent(s)' list box.

Example of Simple and Multiple Regression

DV(Effect)

IV(Cause)

Model Summary

.492a .242 .222 14.73484

Model

1

R R SquareAdjusted R

SquareStd. Error ofthe Estimate

Predictors: (Constant), BOOKSa.

SPSS Output:Part 1: First Part Shown

Multiple R

R Squared =Percent Variance

Explained(0.49 × 0.49)

Corrects for small n

ANOVAb

2633.513 1 2633.513 12.130 .001a

8250.387 38 217.115

10883.900 39

Regression

Residual

Total

Sum ofSquares df Mean Square F Sig.

Predictors: (Constant), BOOKSa.

Dependent Variable: GRADEb.

SPSS Output:Part 2: ANOVA

We’ll ignore this part

SPSS Output:Part 3: The Coefficients

Almost all of this is important. Here we show one Independent variable.

Coefficientsa

52.075 4.035 12.905 .000

5.737 1.647 .492 3.483 .001

(Constant)

BOOKS

Model

1

B Std. Error

UnstandardizedCoefficients

Beta

StandardizedCoefficients

t Sig.

Dependent Variable: GRADEa.

SPSS Output:Part 3(i): The Coefficents - B

• B for books is the increase in grade when you read one more book

• Constant is the estimated grade when you read no (0) books.

• B is shown for each independent variable and the constant.

Coefficientsa

52.075

5.737

(Constant)

BOOKS

Model

1

B

Unstandardized

Coefficients


Prediction Equation

• Estimating the DV

• OR:

DV=B×IV+C

527.5 BooksMarks

Y = BX + C

Add a Line

0 1 2 3 4

80

60

40

20

++

++

+

Here we can draw the line for the

Equation.These are the predicted Values—or best fit line.

SPSS Output:Part 3: The Coefficients

Sig. tests the null hypotheses that B is equal to 0. This is a two-tail test. For directional hypotheses, Divide by 2 to get the sig. level. Two-tail--the B for BOOKs is sig. at the .001 level--about one in 1/000 times wouldwe observe a B as large + or – if there were no relationship Between BOOKS and grades.

Coefficientsa

52.075 4.035 12.905 .000

5.737 1.647 .492 3.483 .001

(Constant)

BOOKS

Model

1

B Std. Error


Beta


t Sig.


• Most of these previous 8 slides were adapted from Jeremy Miles notes on line.

• Now let’s look at explicating a bivariate relationship with a third variable.

Explicating a bivariate relationship with a third variable

A misspecified relationship is when the magnitude or direction of the relationship you observe between a and b is not due to a causing b, but to c partly or wholly causing both a and b. When you control for c the relationship between a and b changes in magnitude or direction.

• Suppose we hypothesize that respondent’s affect for Clinton (thermometer score) causes their affect for Gore (thermometer score).

• But we wish to consider the alternative explanation that partisanship is a cause of both. By ignoring the effect of partisanship on both we can overestimate the effect of feelings towards Clinton impacting feelings towards Gore

Here we might find:

C G++

P

C G

+ +

+

Here we would have overestimated the impact of C on G. C does cause G, but controlling for P we realize the effect is less than we initially thought.

Model Summary

.732a .536 .536 19.105Model1

R R SquareAdjustedR Square

Std. Error ofthe Estimate

Predictors: (Constant), Post:Thermometer Bill Clintona.

Coefficientsa

17.489 1.006 17.388 .000

.689 .016 .732 42.054 .000

(Constant)

Post:ThermometerBill Clinton

Model1

B Std. Error


Beta


t Sig.

Dependent Variable: Post:Thermometer Al Gorea.

C G++

•

Model Summary

.758a .574 .573 18.372Model1



Predictors: (Constant), Party ID: 3 categories,Post:Thermometer Bill Clinton

a.

Coefficientsa

40.952 2.249 18.208 .000

.560 .019 .597 29.003 .000

-8.575 .746 -.236 -11.491 .000

(Constant)


Party ID: 3 categories

Model1

B Std. Error


Beta


t Sig.


• So yes we did overestimate the effect of Clinton on Gore’s thermometer score, but the effect of Clinton on Gore is still quite substantial, and statistically sig. at the .01 level.

• The coefficient on Clinton is reduced from .689 to .560.

• The first equation: G=.689 C + 17.489 becomes: G= .560 C – 8.575 P + 40.952.

• Note: what assumption was I making about party id to have included it in this equation when I used party3? (R=3, I=2, D=1).

• What would you predict G to be for a Dem who rated Clinton at 60?

• G= .560 C – 8.575 P + 40.952.• What would you predict G to be for a Dem (P=1)

who rated Clinton at 60?

• G=.560 * 60 – 8.575 * 1 + 40.952.• G=66• For an Independent, G=57• For a Republican, G=49

Now we might also have started by examining the effect of partisanship on Gore’s thermometer score and then asking whether Clinton’s score was an intervening variable.

a

P C G

P causes G. All or some of the way P causes G is through C.

Pty Gore

Pty Clinton Gore

•

Model Summary

.579a .336 .335 22.932Model1



Predictors: (Constant), Party ID: 3 categoriesa.

Coefficientsa

94.947 1.574 60.305 .000

-21.016 .761 -.579 -27.612 .000

(Constant)


Model1

B Std. Error


Beta


t Sig.


•

Model Summary

.758a .574 .573 18.372Model1



Predictors: (Constant), Party ID: 3 categories,Post:Thermometer Bill Clinton

a.

Coefficientsa

40.952 2.249 18.208 .000

.560 .019 .597 29.003 .000

-8.575 .746 -.236 -11.491 .000

(Constant)



Model1

B Std. Error


Beta


t Sig.


• Most, but not all, of the impact of party on Gore’s thermometer score is due to Clinton’s score. Perception of Clinton mostly explains the way in which party affects perception of Gore

• Remember party is still the cause, we are looking at the mechanism.

Now there is a danger that there is a reciprocal relationship. Perhaps Gore also causes perception of Clinton. We are assuming that perception of Clinton is more important and dominant in this relationship. A simple correlation doesn’t give us the answer—we are making an assumption.

This we don’t think this:

But rather this:

C G

C G

3D Relationship

3D Linear Relationship

0

Multiple Causes (Enhancement): Two variables may be causes of a third variable, while the two are unrelated to each other.

Turning to the legislative data set: Suppose we think that states with higher levels of average education are more likely to elect women to the state legislature either because more women are likely to run or because electorates are more likely to vote for the ones that do.

Suppose you also hypothesize that women are more likely to be elected to lower rather than upper chambers.

E=% college ed in state; C=chamber (2=upper)(1=lower);

W=% women in chamber C

E W+

E W+

Now lets look at the correlations among these three variables

• Correlations

1 -.003 -.250**

.489 .006

99 99 99

-.003 1 .451**

.489 .000

99 99 99

-.250** .451** 1

.006 .000

99 99 99

Pearson Correlation

Sig. (1-tailed)

N

Pearson Correlation

Sig. (1-tailed)

N

Pearson Correlation

Sig. (1-tailed)

N

chamber

colleg_1

pctwch_1

chamber colleg_1 pctwch_1

Correlation is significant at the 0.01 level (1-tailed).**.

•

Model Summary

.451a .203 .195 .08032Model1



Predictors: (Constant), colleg_1a.

Coefficientsa

-.036 .047 -.750 .455

.009 .002 .451 4.970 .000

(Constant)

colleg_1

Model1

B Std. Error


Beta


t Sig.

Dependent Variable: pctwch_1a.

Model Summary

.514a .265 .249 .07755Model1



Predictors: (Constant), chamber, colleg_1a.

Coefficientsa

.031 .051 .609 .544

.009 .002 .450 5.140 .000

-.044 .016 -.248 -2.839 .006

(Constant)

colleg_1

chamber

Model1

B Std. Error


Beta


t Sig.


Now let’s look at a misspecified relationship:

P Wo

S

P W

- -

-

Here we would thought that professionalization (P) had no effect on the percent of women in the chamber (W). But when we control for South (S) we see that there may be an effect of prof that was concealed because of the relationship Southern state region and both P and W.

Model Summary

.017a .000 -.010 .08995Model1



Predictors: (Constant), prof1_1a.

Coefficientsa

.198 .013 14.795 .000

-.006 .036 -.017 -.172 .864

(Constant)

prof1_1

Model1

B Std. Error


Beta


t Sig.


First I computed a var for southern state:

compute south=0.if (state eq 'AL' or state eq 'AR' or state eq 'FL' or state eq 'GA' or state eq 'KY‘ or state eq 'LA' or state eq 'MS' or state eq 'NC' or state eq 'OK' or state eq 'SC' or state eq 'TN' or state eq 'TX' or state eq 'VA')south=1.

Correlations

1 -.545** -.017

.000 .432

99 99 99

-.545** 1 -.192*

.000 .029

99 99 99

-.017 -.192* 1

.432 .029

99 99 99

Pearson Correlation

Sig. (1-tailed)

N

Pearson Correlation

Sig. (1-tailed)

N

Pearson Correlation

Sig. (1-tailed)

N

pctwch_1

south

prof1_1

pctwch_1 south prof1_1

Correlation is significant at the 0.01 level (1-tailed).**.

Correlation is significant at the 0.05 level (1-tailed).*.

S

P W

- -

-

Model Summary

.559a .312 .298 .07500Model1



Predictors: (Constant), south, prof1_1a.

Coefficientsa

.239 .013 18.719 .000

-.045 .031 -.126 -1.466 .146

-.115 .017 -.569 -6.598 .000

(Constant)

prof1_1

south

Model1

B Std. Error


Beta


t Sig.


Model Summary

.650a .423 .398 .06942Model1



Predictors: (Constant), colleg_1, chamber, prof1_1,south

a.

Coefficientsa

.173 .054 3.184 .002

-.054 .029 -.151 -1.886 .062

-.091 .019 -.448 -4.899 .000

-.045 .014 -.252 -3.220 .002

.005 .002 .251 2.751 .007

(Constant)

prof1_1

south

chamber

colleg_1

Model1

B Std. Error


Beta


t Sig.


15. Multiple Regression

Documents

Transcript of 15. Multiple Regression